Hostname: page-component-5f745c7db-6bmsf Total loading time: 0 Render date: 2025-01-06T23:24:50.578Z Has data issue: true hasContentIssue false
  • English
  • Français

Identifiability of Hidden Markov Models for Learning Trajectories in Cognitive Diagnosis

Published online by Cambridge University Press:  01 January 2025

Ying Liu ,
Steven Andrew Culpepper Open the ORCID record for Steven Andrew Culpepper [Opens in a new window]  and
Yuguo Chen Open the ORCID record for Yuguo Chen [Opens in a new window]
Ying Liu
Affiliation:
University of Illinois at Urbana-Champaign
Steven Andrew Culpepper*
Affiliation:
University of Illinois at Urbana-Champaign
Yuguo Chen
Affiliation:
University of Illinois at Urbana-Champaign
*
Correspondence should be made to Steven Andrew Culpepper, Department of Statistics, University of Illinois at Urbana-Champaign, Computing Applications Building, Room 152, 605 E. Springfield Ave., Champaign, IL 61820, USA. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Hidden Markov models (HMMs) have been applied in various domains, which makes the identifiability issue of HMMs popular among researchers. Classical identifiability conditions shown in previous studies are too strong for practical analysis. In this paper, we propose generic identifiability conditions for discrete time HMMs with finite state space. Also, recent studies about cognitive diagnosis models (CDMs) applied first-order HMMs to track changes in attributes related to learning. However, the application of CDMs requires a known Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\varvec{Q}$$\end{document}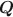 matrix to infer the underlying structure between latent attributes and items, and the identifiability constraints of the model parameters should also be specified. We propose generic identifiability constraints for our restricted HMM and then estimate the model parameters, including the Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\varvec{Q}$$\end{document} 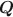matrix, through a Bayesian framework. We present Monte Carlo simulation results to support our conclusion and apply the developed model to a real dataset.

Keywords

cognitive diagnosis modelDINA modelgeneric identifiabilityhidden Markov model
Type
Theory and Methods
Information
Psychometrika , Volume 88 , Issue 2 , June 2023 , pp. 361 - 386
Copyright
Copyright © 2023 The Author(s) under exclusive licence to The Psychometric Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allman, E. S.,Matias, C., &Rhodes, J. A.(2009).Identifiability of parameters in latent structure models with many observed variables.The Annals of Statistics,37(6A),3099–3132.CrossRefGoogle Scholar
Baras, J. S.,Finesso, L.Duncan, T. E., &Pasik-Duncan, B.(1992).Consistent estimation of the order of hidden Markov chains.Stochastic theory and adaptive control,Berlin & Heidelberg:Springer.26–39.CrossRefGoogle Scholar
Blasiak, S., & Rangwala, H. (2011). A hidden Markov model variant for sequence classification. In: Proceedings of the twenty-second international joint conference on artificial intelligence - volume two ( 1192–1197). AAAI Press.Google Scholar
Bonhomme, S.,Jochmans, K., &Robin, J. M.(2016).Estimating multivariate latent-structure models.The Annals of Statistics,44(2),540–563.CrossRefGoogle Scholar
Brooks, S. P., &Gelman, A.(1998).General methods for monitoring convergence of iterative simulations.Journal of Computational and Graphical Statistics,7(4),434–455.CrossRefGoogle Scholar
Chen, Y.,Culpepper, S.,Chen, Y., &Douglas, J.(2018).Bayesian estimation of the DINA Q matrix.Psychometrika,83(1),89–108.CrossRefGoogle ScholarPubMed
Chen, Y., Culpepper, S. A., & Liang, F. (2020). A sparse latent class model for cognitive diagnosis, Psychometrika, 85, 121–153.CrossRefGoogle Scholar
Chen, Y.,Culpepper, S.,Wang, S., &Douglas, J.(2018).A hidden Markov model for learning trajectories in cognitive diagnosis with application to spatial rotation skills.Applied Psychological Measurement,42(1),5–23.CrossRefGoogle ScholarPubMed
Chen, Y.,Liu, J.,Xu, G., &Ying, Z.(2015).Statistical analysis of Q-matrix based diagnostic classification models.Journal of the American Statistical Association,110(510),850–866.CrossRefGoogle Scholar
Chen, Y.,Liu, Y.,Culpepper, S. A., &Chen, Y.(2021).Inferring the number of attributes for the exploratory DINA model.Psychometrika,86(1),30–64.CrossRefGoogle ScholarPubMed
Chiu, C. Y.,Douglas, J., &Li, X.(2009).Cluster analysis for cognitive diagnosis: Theory and applications.Psychometrika,74,633–665.CrossRefGoogle Scholar
Cox, D. A.,Little, J., &O’Shea, D.(2015).Ideals, varieties, and algorithms,New York:Springer.CrossRefGoogle Scholar
Crouse, M. S.,Nowak, R. D., &Baraniuk, R. G.(1998).Wavelet-based statistical signal processing using hidden Markov models.IEEE Transactions on Signal Processing,46(4),886–902.CrossRefGoogle Scholar
Culpepper, S. A.(2015).Bayesian estimation of the DINA model with Gibbs sampling.Journal of Educational and Behavioral Statistics,40(5),454–476.CrossRefGoogle Scholar
De La Torre, J.(2011).The generalized DINA model framework.Psychometrika,76(2),179–199.CrossRefGoogle Scholar
Gu, Y., &Xu, G.(2021).Sufficient and necessary conditions for the identifiability of the Q-matrix.Statistica Sinica,31,449–472.Google Scholar
Haertel, E. H.(1989).Using restricted latent class models to map the skill structure of achievement items.Journal of Educational Measurement,26(4),301–321.CrossRefGoogle Scholar
Heller, J., &Wickelmaier, F.(2013).Minimum discrepancy estimation in probabilistic knowledge structures.Electronic Notes in Discrete Mathematics,42,49–56.CrossRefGoogle Scholar
Henson, R. A.,Templin, J. L., &Willse, J. T.(2009).Defining a family of cognitive diagnosis models using log-linear models with latent variables.Psychometrika,74(2),191–210.CrossRefGoogle Scholar
Junker, B. W., &Sijtsma, K.(2001).Cognitive assessment models with few assumptions, and connections with nonparametric item response theory.Applied Psychological Measurement,25(3),258–272.CrossRefGoogle Scholar
Khatri, C. G., &Rao, C. R.(1968).Solutions to some functional equations and their applications to characterization of probability distributions.Sankhya: The Indian Journal of Statistics, Series A,30(2),167–180.Google Scholar
Kruskal, J.(1977).Three-way arrays: Rank and uniqueness of trilinear decompositions, with application to arithmetic complexity and statistics.Linear Algebra and its Applications,18,95–138.CrossRefGoogle Scholar
Lathauwer, L. D.,Moor, B. D., &Vandewalle, J.(2004).Computation of the canonical decomposition by means of a simultaneous generalized schur decomposition.SIAM Journal on Matrix Analysis and Applications,26,295–327.CrossRefGoogle Scholar
Matsaglia, G., &Styan, G. PH.(1974).Equalities and inequalities for ranks of matrices.Linear and Multilinear Algebra,2(3),269–292.CrossRefGoogle Scholar
Paz, A.Paz, A.(1971).Stochastic Sequential Machines.Introduction to probabilistic automata Academic Press.1–66.Google Scholar
Petrie, T.(1969).Probabilistic functions of finite state Markov chains.The Annals of Mathematical Statistics,40(1),97–115.CrossRefGoogle Scholar
Sipos, I. R.,Ceffer, A., &Levendovszky, J.(2017).Parallel optimization of sparse portfolios with AR-HMMs.Computational Economics,49,563–578.CrossRefGoogle Scholar
Von Davier, M.(2008).A general diagnostic model applied to language testing data.British Journal of Mathematical and Statistical Psychology,61(2),287–307.CrossRefGoogle ScholarPubMed
Xu, G.(2017).Identifiability of restricted latent class models with binary responses.Annals of Statistics,45(2),675–707.CrossRefGoogle Scholar