Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2025-01-06T00:20:56.740Z Has data issue: false hasContentIssue false
  • English
  • Français

Generating Multivariate Ordinal Data via Entropy Principles

Published online by Cambridge University Press:  01 January 2025

Yen Lee  and
David Kaplan
Yen Lee*
Affiliation:
University of Wisconsin - Madison
David Kaplan
Affiliation:
University of Wisconsin - Madison
*
Correspondence should be made to Yen Lee, Department of Educational Psychology, University of Wisconsin - Madison, 859 Education Sciences, 1025 W. Johnson Street, Madison, WI53706-1796, USA. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

When conducting robustness research where the focus of attention is on the impact of non-normality, the marginal skewness and kurtosis are often used to set the degree of non-normality. Monte Carlo methods are commonly applied to conduct this type of research by simulating data from distributions with skewness and kurtosis constrained to pre-specified values. Although several procedures have been proposed to simulate data from distributions with these constraints, no corresponding procedures have been applied for discrete distributions. In this paper, we present two procedures based on the principles of maximum entropy and minimum cross-entropy to estimate the multivariate observed ordinal distributions with constraints on skewness and kurtosis. For these procedures, the correlation matrix of the observed variables is not specified but depends on the relationships between the latent response variables. With the estimated distributions, researchers can study robustness not only focusing on the levels of non-normality but also on the variations in the distribution shapes. A simulation study demonstrates that these procedures yield excellent agreement between specified parameters and those of estimated distributions. A robustness study concerning the effect of distribution shape in the context of confirmatory factor analysis shows that shape can affect the robust χ2\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\chi ^2$$\end{document}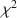 and robust fit indices, especially when the sample size is small, the data are severely non-normal, and the fitted model is complex.

Keywords

Non-normal data generationEntropyDiscrete data
Type
Original Paper
Information
Psychometrika , Volume 83 , Issue 1 , March 2018 , pp. 156 - 181
Copyright
Copyright © 2018 The Psychometric Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Electronic supplementary material The online version of this article (https://doi.org/10.1007/s11336-018-9603-3) contains supplementary material, which is available to authorized users.

References

Asparouhov, T., Muthén, B. (2010). Simple second order chi-square correction. Retrieved from Mplus website: http://www.statjnodel.com/dowrJoad/WLSMV_new_chi21.Google Scholar
Babakus, E., Ferguson, E.J., Joreskog, K.G., (1987). The sensitivity of confirmatory maximum likelihood factor analysis to violations of measurement scale and distributional assumptions, Journal of Marketing Research, 24, 222–228.CrossRefGoogle Scholar
Blair, R.C., (1981). A reaction to consequence of failure to meet assumptions underlying fixed effects analysis of variance and covariance, Review of Educational Research, 51, 499–507.CrossRefGoogle Scholar
Bollen, K.A., (1989). Structural equations with latent variables New York: John Wiley and Sons Inc..CrossRefGoogle Scholar
Bradley, J.V., (1982). The insidious L-shaped distribution, Bulletin of the Psychonomic Society, 20, 85–88.CrossRefGoogle Scholar
Browne, M.W., Cudeck, R., (1993). Alternative ways of assessing model fit. In Bollen, K.A., Long, J.S.(Eds.), Testing Structural Equation Models, Thousand Oaks, CA: Sage Publications, 136–162.Google Scholar
DiStefano, C., Morgan, G.B., (2014). A comparison of diagonal weighted least squares robust estimation techniques for ordinal data, Structural Equation Modeling: A Multidisciplinary Journal, 213, 425–438.CrossRefGoogle Scholar
Ethington, C.A., (1987). The robustness of LISREL estimates in structural equation models with categorical variables, The Journal of Experimental Education, 55, 80–88.CrossRefGoogle Scholar
Fleishman, A.I., (1978). A method for simulating non-normal distributions, Psychometrika, 43, 521–532.CrossRefGoogle Scholar
Flora, D.B., Curran, P.J., (2004). An empirical evaluation of alternative methods of estimation for confirmatory factor analysis with ordinal data, Psychological Methods, 9, 466–4913153362.CrossRefGoogle ScholarPubMed
Genz, A., (1992). Numerical computation of multivariate normal probabilities, Journal of computational and graphical statistics, 1(2) 141–149.CrossRefGoogle Scholar
Genz, A., Bretz, F., (2002). Comparison of methods for the computation of multivariate t probabilities, Journal of Computational and Graphical Statistics, 11(4) 950–971.CrossRefGoogle Scholar
Genz, A., Bretz, F., Miwa, T., Mi, X, Leisch, F., Scheipl, F., Hothorn, T., (2015). mvtnorm: Multivariate normal and t distributions. http://CRAN.R-project.org/package=mvtnorm (R package version 1.0-3).Google Scholar
Golan, A., Judge, G., Miller, D., (1997). Maximum entropy econometrics: Robust estimation with limited data Chichester: Wiley.Google Scholar
Headrick, T.C., (2010). Statistical simulation: Power method polynomials and other transformations Boca Raton, FL: Chapman and Hall.Google Scholar
Headrick, T.C., Sawilosky, S.S., (1999). Simulating correlated multivariate nonnormal distributions: Extending the Fleishman power method, Psychometrika, 64, 25–35.CrossRefGoogle Scholar
Hipp, J.R., Bollen, K.A., (2003). Model fit in structural equation models with censored, ordinal, and dichotomous variables: Testing vanishing tetrads, Sociological Methodology, 33, 267–305.CrossRefGoogle Scholar
Hooper, D., Coughlan, J., Mullen, M.R., (2008). Structural equation modelling: Guidelines for determining model fit, Electronic Journal of Business Research Methods, 6 53–60.Google Scholar
Jaynes, E.T., (1957). Information theory and statistical mechanics, Physics Review, 106, 620–630.CrossRefGoogle Scholar
Jaynes, E.T., (1982). On the rationale of maximum-entropy methods, IEEE, 70, 939–952.CrossRefGoogle Scholar
Jorgensen, T., (2016). lavaanTabular Lavaan output .scaled —.robust. https://groups.google.com/forum/#!topic/lavaan/rGitXu9h9zY (Online; accessed February 19, 2017).Google Scholar
Kapur, J.N., Kesavan, H.K., (1992). Entropy optimization principles with applications, Boston: Academic Press.CrossRefGoogle Scholar
Kullback, S., Leibler, R., (1951). On information and sufficiency, Annals of Mathematical Statistics, 22, 79–86.CrossRefGoogle Scholar
Lee, Y., (2010). Generation of non-normal approximated discrete random variables. Master’s thesis, National Chengchi University, Taipei, Taiwan.Google Scholar
Madsen, K., Nielsen, H. B., Tingleff, O., (2004). Optimization with constraints. LyngbyIMM, Technical University of Denmark. http://orbit.dtu.dk/files/2721110/imm4213.pdf.Google Scholar
Mair, P., Satorra, A., Bentler, P.M., (2012). Generating nonnormal multivariate data using copulas: Applications to sem, Multivariate Behavioral Research, 47, 547–565.CrossRefGoogle ScholarPubMed
Mattson, S., (1997). How to generate non-normal data for simulation of structural equation models, Multivariate Behavioral Research, 32, 355–373.CrossRefGoogle ScholarPubMed
Micceri, T., (1989). The unicorn, the normal curve, and other improbable creatures, Psychological Bulletin, 105, 156–166.CrossRefGoogle Scholar
Muthén, B., (1983). Latent variable structural equation modeling with categorical data, Journal of Econometrics, 22, 486–5.CrossRefGoogle Scholar
Muthén, B., (1984). A general structural equation model with dichotomous, ordered categorical, and continuous latent variable indicators, Psychometrika, 49, 115–132.CrossRefGoogle Scholar
Muthén, B., Kaplan, D., (1985). A comparison of some methodologies for the factor analysis of non-normal Likert variables, British Journal of Mathematical and Statistical Psychology, 38, 171–189.CrossRefGoogle Scholar
Muthén, B., Kaplan, D., (1992). A comparison of some methodologies for the factor analysis of non-normal likert variables: A note on the size of the model, British Journal of Mathematical and Statistical Psychology, 45, 19–30.CrossRefGoogle Scholar
Nocedal, J., Wright, S., (2006). Numerical optimization, Berlin: Springer.Google Scholar
Olsson, U., (1979). On the robustness of factor analysis against crude classification of the observations, Multivariate Behavioral Research, 14, 485–500.CrossRefGoogle ScholarPubMed
Pearson, E.S., Please, N.W., (1975). Relation between the shape of population distribution and the robustness of four simple test statistics, Biometrika, 62, 223–241.CrossRefGoogle Scholar
Core, R Team. (2014). R: A Language and Environment for Statistical Computing Vienna, Austria. http://www.R-project.org/.Google Scholar
Ramachandran, K.M., Tsokos, C.P., Mathematical statistics with applications 2009 Burlington, MA: Elsevier.Google Scholar
Rohatgi, V.K., Székely, G.J., (1989). Sharp inequalities between skewness and kurtosis, Statistics & Probability Letters, 84, 297–299.CrossRefGoogle Scholar
Rosseel, Y., 2012. lavaan: An R package for structural equation modeling. Journal of Statistical Software4821-36. http://jstatsoft.org/v48/i02/.CrossRefGoogle Scholar
Ruscio, J., Kaczetow, W., (2008). Simulating multivariate nonnormal data using an iterative technique, Multivariate Behavioral Research, 48, 355–381.CrossRefGoogle Scholar
Shannon, C.E., (1948). A mathematical theory of communication, The Bell System Technical Journal, 27(3) 379–423.CrossRefGoogle Scholar
Varadhan, R., (2015). alabama: Constrained nonlinear optimization. http://CRAN.R-project.org/package=alabama (R package version 2015.3-1).Google Scholar
Weng, L., Cheng, C., (2004). Effects of response order on Likert-type scale, Educational and Psychological Measurement, 60, 908–924.CrossRefGoogle Scholar
Wilkins, J.E., (1944). A note on skewness and kurtosis, The Annal of Mathematical Statistic, 15, 333–335.CrossRefGoogle Scholar
Wu, N., (1997). The maximum entropy method, New York: Springer.CrossRefGoogle Scholar
Yang-Wallentin, F., Joreskog, K., Luo, H., (2010). Confirmatory factor analysis of ordinal variables with misspecified models, Structural Equation Modeling, 17, 392–423.CrossRefGoogle Scholar
Zellner, A., Highfield, R.A., (1988). Calculation of maximum entropy distributions and approximation of marginal posterior distributions, Journal of Econometrics, 37, 195–209.CrossRefGoogle Scholar
Supplementary material: File

Lee and Kaplan supplementary material

Lee and Kaplan supplementary material
Download Lee and Kaplan supplementary material(File)
File 6.7 KB