Article contents
Coefficient Alpha and the Internal Structure of Tests
Published online by Cambridge University Press: 01 January 2025
Abstract
A general formula (α) of which a special case is the Kuder-Richardson coefficient of equivalence is shown to be the mean of all split-half coefficients resulting from different splittings of a test. α is therefore an estimate of the correlation between two random samples of items from a universe of items like those in the test. α is found to be an appropriate index of equivalence and, except for very short tests, of the first-factor concentration in the test. Tests divisible into distinct subtests should be so divided before using the formula. The index \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\bar r_{ij} $$\end{document}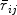 , derived from α, is shown to be an index of inter-item homogeneity. Comparison is made to the Guttman and Loevinger approaches. Parallel split coefficients are shown to be unnecessary for tests of common types. In designing tests, maximum interpretability of scores is obtained by increasing the first-factor concentration in any separately-scored subtest and avoiding substantial group-factor clusters within a subtest. Scalability is not a requisite.
, derived from α, is shown to be an index of inter-item homogeneity. Comparison is made to the Guttman and Loevinger approaches. Parallel split coefficients are shown to be unnecessary for tests of common types. In designing tests, maximum interpretability of scores is obtained by increasing the first-factor concentration in any separately-scored subtest and avoiding substantial group-factor clusters within a subtest. Scalability is not a requisite.
- Type
- Original Paper
- Information
- Copyright
- Copyright © 1951 The Psychometric Society
Footnotes
The assistance of Dora Damrin and Willard Warrington is gratefully acknowledged. Miss Damrin took major responsibility for the empirical studies reported. This research was supported by the Bureau of Research and Service, College of Education.
References
- 26046
- Cited by


