Scientific Background Categorization decisions are important in almost all aspects of our lives—whether it is a friend or a foe, edible or non-edible, the word /bat/ or /hat/, etc. The underlying cognitive dynamics are being actively studied through extensive ongoing research (Glimcher & Fehr, Reference Glimcher and Fehr2013; Gold & Shadlen, Reference Gold and Shadlen2007; Heekeren et al., Reference Heekeren, Marrett, Bandettini and Ungerleider2004; Purcell, Reference Purcell2013; Schall, Reference Schall2001; Smith & Ratcliff, Reference Smith and Ratcliff2004).
In typical multi-category decision tasks, the brain accumulates sensory evidence in order to make a categorical decision. This accumulation process is reflected in the increasing firing rates at local neural populations associated with different decisions. A decision is taken when neural activity in one of these populations reaches a particular threshold level. The decision category that is finally chosen is the one whose decision threshold is crossed first (Brody & Hanks, Reference Brody and Hanks2016; Gold & Shadlen, Reference Gold and Shadlen2007). Changes in evidence accumulation rates and decision thresholds can be induced by differences in task difficulty and/or cognitive function (Cavanagh et al., Reference Cavanagh, Wiecki, Cohen, Figueroa, Samanta, Sherman and Frank2011; Ding & Gold, Reference Ding and Gold2013). Decision-making is also regulated by demands on both the speed and accuracy of the task (Bogacz et al., Reference Bogacz, Wagenmakers, Forstmann and Nieuwenhuis2010; Milosavljevic et al., Reference Milosavljevic, Malmaud, Huth, Koch and Rangel2010).
Understanding the brain activity patterns for different decision alternatives is a key scientific interest in modeling brain mechanisms underlying decision-making. Statistical approaches with biologically interpretable parameters that further allow probabilistic clustering of the parameters (Lau & Green, Reference Lau and Green2007; Wade, Reference Wade2023) associated with different competing choices can facilitate such inference, the parameters clustering together indicating similar behavior and difficulty levels.
Drift-Diffusion Models A biologically interpretable joint model for decision response accuracies and associated response times is obtained by imitating the underlying evidence accumulation mechanisms using latent drift-diffusion processes racing toward their respective boundaries, the process reaching its boundary first producing the final observed decision and the time taken to reach this boundary giving the associated response time (Fig. 1a) (Usher & McClelland, Reference Usher and McClelland2001).
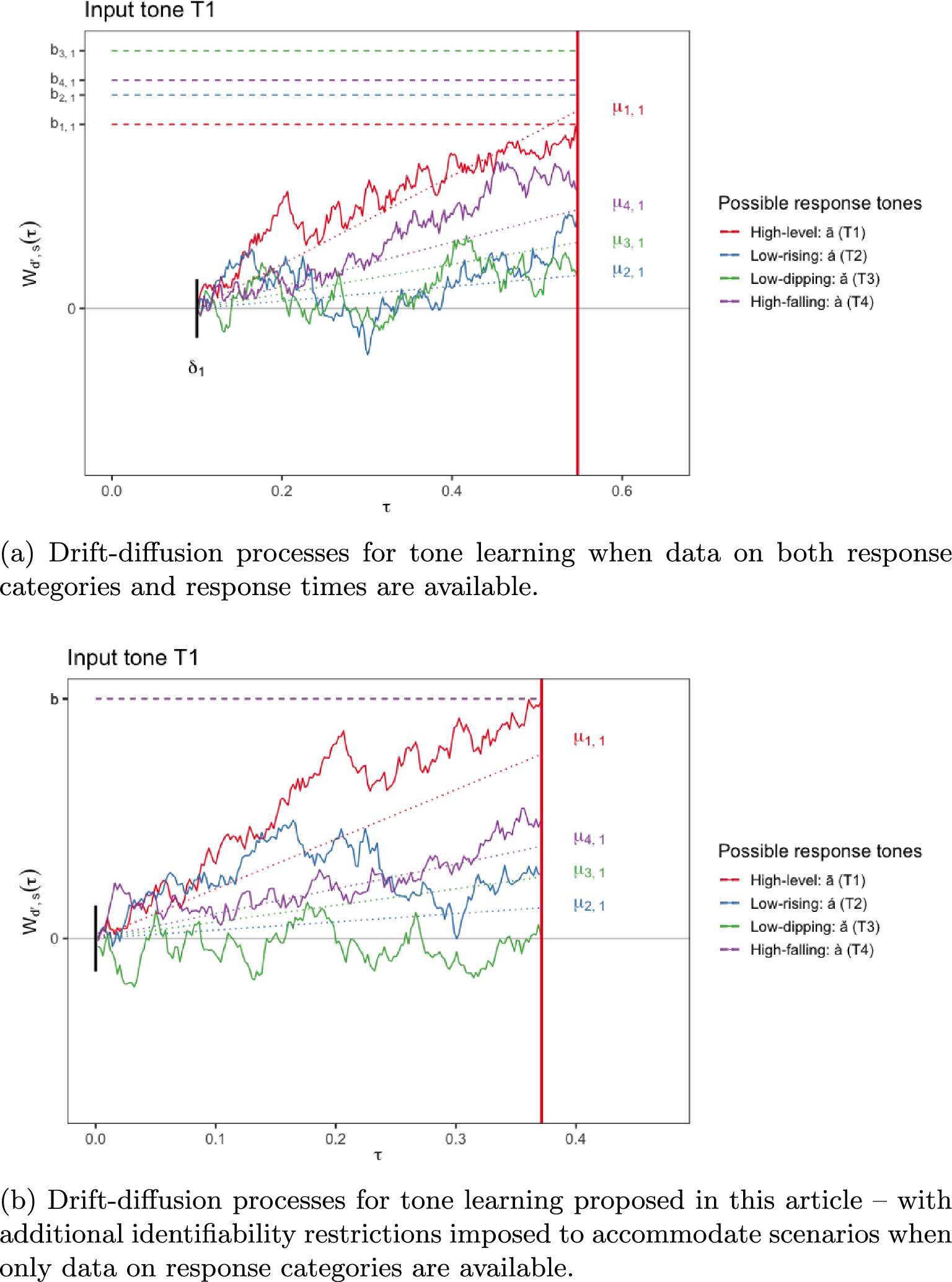
Figure 1 Drift-diffusion model for tone learning. The tones {T1, T2, T3, T4} represent the different categories; s denotes an input category,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d^{\prime }$$\end{document}
![]() the different possible response categories, and d the final response category. Here we are illustrating a single trial with input tone T1 (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$s = 1$$\end{document}
the different possible response categories, and d the final response category. Here we are illustrating a single trial with input tone T1 (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$s = 1$$\end{document}
![]() ) that was eventually correctly identified (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1$$\end{document}
) that was eventually correctly identified (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1$$\end{document}
![]() ). a Shows a process whose parameters can be inferred from data on both response categories and response times. Here, after an initial
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\delta _{s}$$\end{document}
). a Shows a process whose parameters can be inferred from data on both response categories and response times. Here, after an initial
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\delta _{s}$$\end{document}
![]() amount of time required to encode an input category s (here T1), the evidence in favor of different possible response categories
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d'$$\end{document}
amount of time required to encode an input category s (here T1), the evidence in favor of different possible response categories
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d'$$\end{document}
![]() accumulates according to latent Wiener diffusion processes
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$W_{d',s}(\tau )$$\end{document}
accumulates according to latent Wiener diffusion processes
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$W_{d',s}(\tau )$$\end{document}
![]() (red, blue, green, and purple) with drifts
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d',s}$$\end{document}
(red, blue, green, and purple) with drifts
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d',s}$$\end{document}
![]() . The decision d (here T1) is eventually taken if the underlying process (here the red one) is the first to reach its decision boundary
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d,s}$$\end{document}
. The decision d (here T1) is eventually taken if the underlying process (here the red one) is the first to reach its decision boundary
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d,s}$$\end{document}
![]() . b shows a process with additional identifiability restrictions (for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d'$$\end{document}
. b shows a process with additional identifiability restrictions (for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d'$$\end{document}
![]() and s,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\delta _{s}=0$$\end{document}
and s,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\delta _{s}=0$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d',s}=b$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d',s}=b$$\end{document}
![]() fixed, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sum _{d'=1}^{d_{0}}\mu _{d',s}=d_{0}$$\end{document}
fixed, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sum _{d'=1}^{d_{0}}\mu _{d',s}=d_{0}$$\end{document}
![]() ) considered in this article which can be inferred from data on response categories alone.
) considered in this article which can be inferred from data on response categories alone.
The literature on drift-diffusion processes for decision-making is rather vast but is mostly focused on simple binary decision scenarios with a single latent diffusion process with two boundaries, one for each of the two decision alternatives (Ratcliff, Reference Ratcliff1978; Ratcliff et al., Reference Ratcliff, Smith, Brown and McKoon2016; Ratcliff & Rouder, Reference Ratcliff and Rouder1998; Ratcliff & McKoon, Reference Ratcliff and McKoon2008; Smith & Vickers, Reference Smith and Vickers1988). Multi-category drift-diffusion models with multiple latent processes are mathematically more easily tractable (Brown & Heathcote, Reference Brown and Heathcote2008; Dufau et al., Reference Dufau, Grainger and Ziegler2012; Kim et al., Reference Kim, Potter, Craigmile, Peruggia and Van Zandt2017; Leite & Ratcliff, Reference Leite and Ratcliff2010; Usher & McClelland, Reference Usher and McClelland2001) but the literature is sparse and focused only on simple static designs.
Learning to make categorization decisions is, however, a dynamic process, driven by perceptual adjustments in our brain and behavior over time. Category learning is thus often studied in longitudinal experiments. To address the need for sophisticated statistical methods for such settings, Paulon et al. (Reference Paulon, Llanos, Chandrasekaran and Sarkar2021) developed an inverse Gaussian distribution-based multi-category longitudinal drift-diffusion mixed model.
Data Requirements and Related Challenges Crucially, measurements on both the final decision categories and the associated response times are needed to estimate the drift and the boundary parameters from conventional drift-diffusion models, including the work by Paulon et al. (Reference Paulon, Llanos, Chandrasekaran and Sarkar2021). Unfortunately, however, researchers often only record the participants’ decision responses as their go-to measure of categorization performance, ignoring the response times (Chandrasekaran et al., Reference Chandrasekaran, Yi and Maddox2014; Filoteo et al., Reference Filoteo, Lauritzen and Maddox2010). Additionally, eliciting accurate response times can be methodologically challenging, e.g., in the case of experiments conducted online, especially during the Covid-19 pandemic (Roark et al., Reference Roark, Smayda and Chandrasekaran2021), or when the response times from participants/patients are unreliable due to motor deficits (Ashby et al., Reference Ashby, Noble, Filoteo, Waldron and Ell2003). Participants may also be asked to delay the reporting of their decisions so that delayed physiological responses that relate to decision-making can be accurately measured (McHaney et al., Reference McHaney, Tessmer, Roark and Chandrasekaran2021). In such cases, the reported response times may not accurately relate to the actual decision times and hence cannot be used in the analysis. As a result, conventional drift-diffusion analysis that requires data on both response accuracies and response times, such as Paulon et al. (Reference Paulon, Llanos, Chandrasekaran and Sarkar2021), cannot be used in such scenarios.
The Research Question The main research question addressed in this article is to see if a new class of drift-diffusion models can be designed for such scenarios which will allow the biologically interpretable drift-diffusion process parameters to be meaningfully recovered from data on input–output category combinations alone.
The Inverse-Probit Model Categorical probability models that build on latent drift-diffusion processes can be useful in providing biologically interpretable inference in data sets comprising input–output categories but no response times. To our knowledge, however, the problem has never been considered in the literature before. We aim to address this remarkable gap in this article.
By integrating out the latent response times from the joint inverse Gaussian drift-diffusion model for response categories and associated response times in Paulon et al. (Reference Paulon, Llanos, Chandrasekaran and Sarkar2021), we can arrive at a natural albeit overparametrized model for the response categories. We refer to this as the ‘inverse-probit’ categorical probability model. This inverse-probit model serves as the starting point for the methodology presented in this article but, as we describe below, it also comes with significant and unique statistical challenges not encountered in the original drift-diffusion model.
Statistical Challenges While scientifically desirable, unfortunately, it is also mathematically impossible to infer both the drifts and the boundaries in the inverse-probit model from data only on the decision accuracies. We must thus have to keep the values of either the drifts or the boundaries fixed and focus on inferring the other.
However, even when we fix either the drift or the decision boundaries, the problem of overparametrization persists. In the absence of response times, only the information on relative frequencies, that is empirical probabilities of taking a decision is available. As the total probability of observing any of the competing decisions is one, the identifiability problem remains for the chosen main parameters of interest, and appropriate remedial constraints need to be imposed.
Setting an arbitrarily chosen category as the reference provides a simple solution widely adopted in categorical probability models but comes with serious limitations, including breaking the symmetry of the problem, potentially making posterior inference sensitive to the specific choice of the reference category (Burgette & Nordheim, Reference Burgette and Nordheim2012; Johndrow et al., Reference Johndrow, Dunson and Lum2013).
By breaking the symmetry of the problem, a reference category also additionally makes it difficult to infer the potential clustering of the model parameters, especially across different panels. To see this, consider a problem with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d_{0}$$\end{document}
![]() categories, with a logistic model for the probabilities
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$p_{s,d^{\prime }}=\hbox {logistic}(\beta _{s,d^{\prime }}),\; s,d^{\prime }\in \{1:d_{0}\}$$\end{document}
categories, with a logistic model for the probabilities
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$p_{s,d^{\prime }}=\hbox {logistic}(\beta _{s,d^{\prime }}),\; s,d^{\prime }\in \{1:d_{0}\}$$\end{document}
![]() , of choosing the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${d^{\prime }}$$\end{document}
, of choosing the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${d^{\prime }}$$\end{document}
![]() th output category for the sth input category. For each input category s, by setting the sth output category as a reference, e.g., by fixing
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta _{s,s} = 0$$\end{document}
th output category for the sth input category. For each input category s, by setting the sth output category as a reference, e.g., by fixing
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta _{s,s} = 0$$\end{document}
![]() , one can then cluster the probabilities of incorrect decision choices,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$p_{s,d^{\prime }}$$\end{document}
, one can then cluster the probabilities of incorrect decision choices,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$p_{s,d^{\prime }}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d^{\prime }\ne s$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d^{\prime }\ne s$$\end{document}
![]() . However, it is not clear how to compare the probabilities across different input categories (i.e., across the four panels in Fig. 2), e.g., how to test the equality of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$p_{1,1}$$\end{document}
. However, it is not clear how to compare the probabilities across different input categories (i.e., across the four panels in Fig. 2), e.g., how to test the equality of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$p_{1,1}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$p_{2,2}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$p_{2,2}$$\end{document}
![]() .
.
Finally, while coming up with solutions for the aforementioned issues, we must also take into consideration the complex longitudinal design of the experiments generating the data. Whatever strategy we devise, it should be amenable to a longitudinal mixed model analysis that ideally allows us to (a) estimate the smoothly varying longitudinal trajectories of the parameters as the participants learn over time, (b) accommodate participant heterogeneity, and (c) compare the estimates at different time points within and between different input categories.
Our Proposed Approach As a first step toward addressing the identifiability issues and related modeling challenges, we keep the boundaries fixed but leave the drift parameters unconstrained. The decision to focus on the drifts is informed by the existing literature on such models cited above where the drifts have almost always been allowed more flexibility. The analysis of Paulon et al. (Reference Paulon, Llanos, Chandrasekaran and Sarkar2021) also showed that it is primarily the variations in the drift trajectories that explain learning while the boundaries remain relatively stable over time.
As a next step toward establishing identifiability, we apply a ‘sum to a constant’ condition on the drifts so that symmetry is maintained in the constrained model.
Implementation of this restriction brings in significant challenges. One possibility is to design a prior on the constraint space, a challenging task in itself. Additionally, posterior computation for such priors would also be extremely complicated in drift-diffusion models. Instead, we conduct inference with an unconstrained prior on the drift parameters and project the samples drawn from the corresponding posterior to the constrained space through a minimal distance mapping.
To adapt this categorical probability model to a longitudinal mixed model setting, we then assume that the drift parameters comprise input-response-category-specific fixed effects and subject-specific random effects, modeling them flexibly by mixtures of locally supported B-spline bases (de Boor, Reference de Boor1978; Eilers & Marx, Reference Eilers and Marx1996) spanning the length of the longitudinal experiment. These effects are thus allowed to evolve flexibly as smooth functions of time (Morris, Reference Morris2015; Ramsay & Silverman, Reference Ramsay and Silverman2007; Wang et al., Reference Wang, Chiou and Müller2016) as the participants get more experience and training in their assigned decision tasks.
We take a Bayesian route to estimation and inference. Carefully exploiting conditional prior-posterior conjugacy as well as our latent variable construction, we design an efficient Markov chain Monte Carlo (MCMC)-based algorithm for approximating the posterior, where sampling the latent response times for each observed response category greatly simplifies the computations.
We evaluate the numerical performance of the proposed approach in extensive simulation studies. We then apply our method to the PTC1 data set described below. These applications illustrate the utility of our method in providing insights into how the drift parameters characterize the rates of accumulation of evidence in the brain evolve over time, differ between input–output category combinations, as well as between individuals.
Differences from Previous Works This article differs in many fundamental ways from all existing works on drift-diffusion models, including Paulon et al. (Reference Paulon, Llanos, Chandrasekaran and Sarkar2021), where response categories and response times were both observed and therefore the drift and boundary parameters could be modeled jointly with no identifiability issues. In contrast, the current work is motivated by scenarios where data on only response categories are available, leading us to the inverse-probit categorical probability model which, with its complex identifiability issues, brings in new unique challenges to performing statistical inference, confining us only to infer the drift parameters on a relative scale, achieved via a novel projection-based approach. The introduction and analysis of the inverse-probit model, addressing the significant new statistical challenges posed by it, ranging across (a) identifiability issues, (b) assessment of intra- and inter-panel similarities, (c) extension to complex longitudinal mixed effects settings to accommodate the motivating applications, (d) computational implementation of these new models, etc. are the novel contributions of this article.
Outline of the Article Section 1 describes our motivating tone learning study. Sections 2 and 3 develop our longitudinal inverse-probit mixed model. Section 4 outlines our computational strategies. Section 5 presents the results of simulation experiments. Section 6 presents the results of the proposed method applied to our motivating PTC1 study. Section 7 concludes the main article with a discussion. Additional details, including Markov chain Monte Carlo (MCMC)-based posterior inference algorithms, are deferred to the supplementary material.
1. The PTC1 Data Set
The PTC1 (pupillometry tone categorization experiment 1) data set is obtained from a Mandarin tone learning study conducted at the Department of Communication Science and Disorders, University of Pittsburgh (McHaney et al., Reference McHaney, Tessmer, Roark and Chandrasekaran2021). Mandarin Chinese is a tonal language, which means that pitch patterns at the syllable level differentiate word meanings. There are four linguistically relevant pitch patterns in Mandarin that make up the four Mandarin tones: high-flat (Tone 1), low-rising (Tone 2), low-dipping (Tone 3), and high-falling (Tone 4). For example, the syllable /ma/ can be pronounced using the four different pitch patterns of the four tones, which would result in four different word meanings. Adult native English speakers typically experience difficulty differentiating between the four Mandarin tones because pitch contrasts at the syllable level are not linguistically relevant to word meanings in English (Wang et al., Reference Wang, Spence, Jongman and Sereno1999, Reference Wang, Jongman and Sereno2003). Thus, Mandarin tones are valid stimuli to examine how non-native speech sounds are acquired, which has implications for second language learning in adulthood. In PTC1, a group of native English-speaking younger adults learned to categorize monosyllabic Mandarin tones in a training task. During a single trial of training, an input tone was presented over headphones, and the participants were instructed to categorize the tone into one of the four tone categories via a button press on a keyboard. Corrective feedback in the form of “Correct” or “Wrong” was then provided on screen. A total of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$n=28$$\end{document}
![]() participants completed the training task across
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T=6$$\end{document}
participants completed the training task across
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T=6$$\end{document}
![]() blocks of training, each block comprising
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$L=40$$\end{document}
blocks of training, each block comprising
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$L=40$$\end{document}
![]() trials. Figure 2 shows the middle 30% quantiles of the proportion of times the response to an input tone was classified into different tone categories over blocks across different subjects, each for the four input tones.
trials. Figure 2 shows the middle 30% quantiles of the proportion of times the response to an input tone was classified into different tone categories over blocks across different subjects, each for the four input tones.
Pupillometry measurements were also taken during each trial. It is commonly used as a metric of cognitive effort during listening because increases in pupil diameter are associated with greater usage of cognitive resources (Parthasarathy et al., Reference Parthasarathy, Hancock, Bennett, DeGruttola and Polley2020; Peelle, Reference Peelle2018; Robison & Unsworth, Reference Robison and Unsworth2019; Winn et al., Reference Winn, Wendt, Koelewijn and Kuchinsky2018; Zekveld et al., Reference Zekveld, Kramer and Festen2011). One issue with pupillary responses however is that they unfold slowly over time. In view of that, unlike standard Mandarin tone training tasks, where the participants hear the input tone, press the keyboard response, and are provided feedback all within a few seconds (Chandrasekaran et al., Reference Chandrasekaran, Yi, Smayda and Maddox2016; Llanos et al., Reference Llanos, McHaney, Schuerman, Yi, Leonard and Chandrasekaran2020; Reetzke et al., Reference Reetzke, Xie, Llanos and Chandrasekaran2018; Smayda et al., Reference Smayda, Chandrasekaran and Maddox2015), in the PTC1 experiment, there was an intentional four-second delay from the start of the input tone to the response prompt screen where participants made their category decision via button press. This four-second delay allows the pupil to dilate in response to hearing the tone and begin to return to baseline before the participant makes a motor response to the button press. During this four-second period, participants have likely already made conscious category decisions. As such, the response times that are recorded in the end are not meaningful measures of their actual decision times.
This presents a critical limitation for using these response times for further analysis. Conventional drift-diffusion analysis that requires data on response times, such as the one presented in Paulon et al. (Reference Paulon, Llanos, Chandrasekaran and Sarkar2021), can no longer be directly applied here. The focus of this article is to see if the drift-diffusion parameters can still be meaningfully recovered from input–output tone categories alone in the PTC1 data.
We found drift-diffusion analysis in the absence of reliable data on response times challenging enough to merit its separate treatment presented here. Relating drift-diffusion parameters to measures of cognitive effort such as pupillometry is another challenging problem that we are pursuing separately elsewhere.
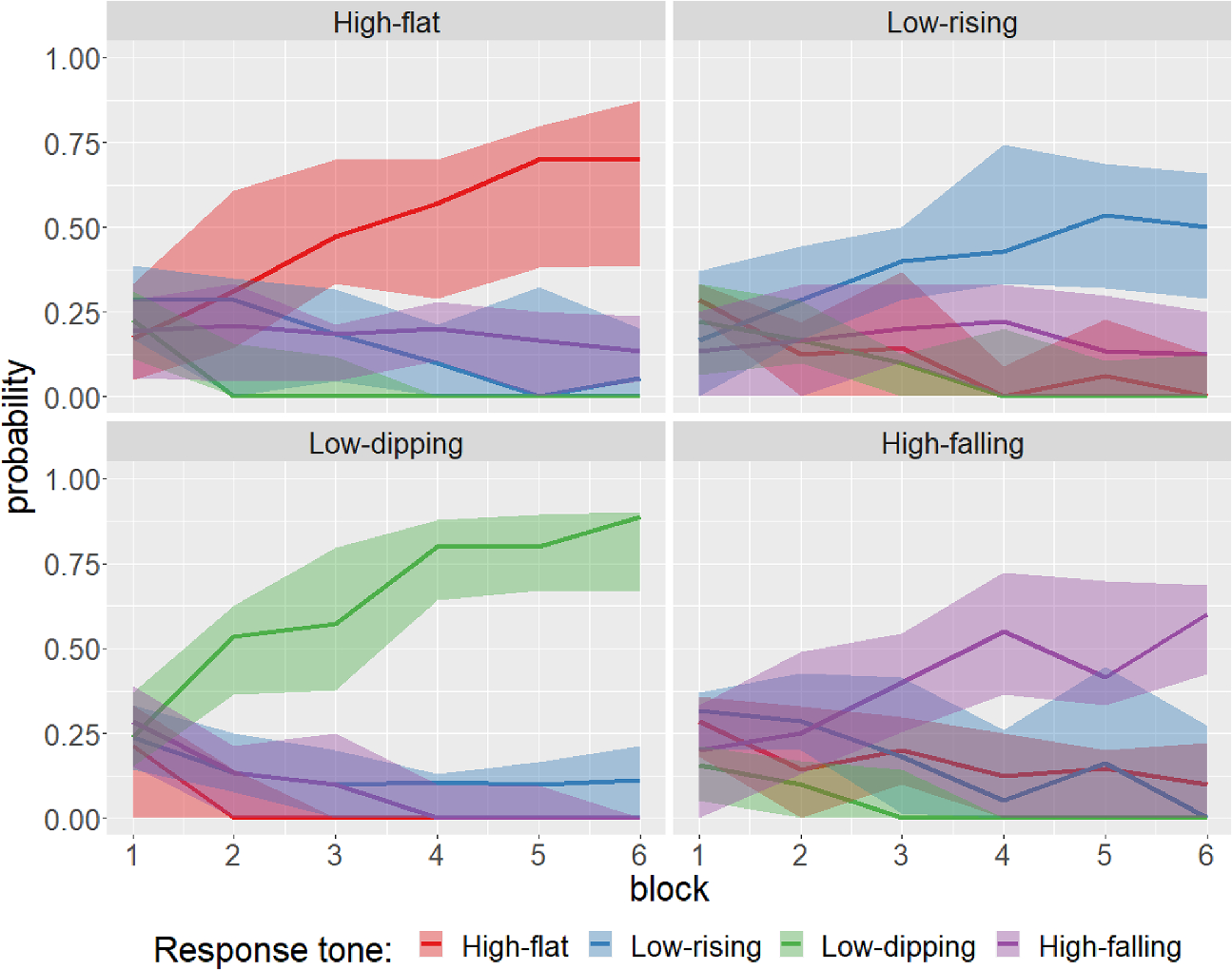
Figure 2 Description of PTC1 data: The proportion of times the response to an input tone was classified into different tone categories over blocks across different subjects, each for the four input tones (indicated in the panel headers). The thick line represents the median performance and the shaded region indicates the corresponding middle 30% quantiles across subjects.
2. Inverse-Probit Model
The starting point for the proposed inverse-probit categorical probability model follows straightforwardly by integrating out the (unobserved) response times from the joint model for response categories and associated response times developed in Paulon et al. (Reference Paulon, Llanos, Chandrasekaran and Sarkar2021). The derivation of this original joint model illustrates its latent drift-diffusion process-based underpinnings (Fig. 1a). Later such construction will also be crucial in understanding the diffusion process-based foundations of the marginal categorical probability model modified with identifiability constraints proposed in this article (Fig. 1b). We therefore present the derivation from Paulon et al. (Reference Paulon, Llanos, Chandrasekaran and Sarkar2021) ditto here which also keeps the main paper self-contained.
To begin with, a Wiener diffusion process
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$W(\tau )$$\end{document}
![]() over domain
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau \in (0,\infty )$$\end{document}
over domain
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau \in (0,\infty )$$\end{document}
![]() can be specified as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$W(\tau ) = \mu \tau + \sigma B(\tau )$$\end{document}
can be specified as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$W(\tau ) = \mu \tau + \sigma B(\tau )$$\end{document}
![]() , where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$B(\tau )$$\end{document}
, where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$B(\tau )$$\end{document}
![]() is the standard Brownian motion,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu $$\end{document}
is the standard Brownian motion,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu $$\end{document}
![]() is the drift rate, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sigma $$\end{document}
is the drift rate, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sigma $$\end{document}
![]() is the diffusion coefficient (Cox & Miller, Reference Cox and Miller1965; Ross et al., Reference Ross, Kelly, Sullivan, Perry, Mercer, Davis, Washburn, Sager, Boyce and Bristow1996). The process has independent normally distributed increments, i.e.,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Delta W(\tau ) = \{W(\tau +\Delta \tau ) - W(\tau )\} \sim \hbox {Normal}(\mu \Delta \tau ,\sigma ^{2} \Delta \tau )$$\end{document}
is the diffusion coefficient (Cox & Miller, Reference Cox and Miller1965; Ross et al., Reference Ross, Kelly, Sullivan, Perry, Mercer, Davis, Washburn, Sager, Boyce and Bristow1996). The process has independent normally distributed increments, i.e.,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Delta W(\tau ) = \{W(\tau +\Delta \tau ) - W(\tau )\} \sim \hbox {Normal}(\mu \Delta \tau ,\sigma ^{2} \Delta \tau )$$\end{document}
![]() , independently from
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$W(\tau )$$\end{document}
, independently from
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$W(\tau )$$\end{document}
![]() . The first passage time of crossing a threshold b,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau = \inf \{\tau ^{\prime }: W(0)=0, W(\tau ^{\prime }) \ge b\}$$\end{document}
. The first passage time of crossing a threshold b,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau = \inf \{\tau ^{\prime }: W(0)=0, W(\tau ^{\prime }) \ge b\}$$\end{document}
![]() , is then distributed according to an inverse Gaussian distribution (Chhikara, Reference Chhikara1988; Lu, Reference Lu1995; Whitmore & Seshadri, Reference Whitmore and Seshadri1987) with mean
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b/\mu $$\end{document}
, is then distributed according to an inverse Gaussian distribution (Chhikara, Reference Chhikara1988; Lu, Reference Lu1995; Whitmore & Seshadri, Reference Whitmore and Seshadri1987) with mean
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b/\mu $$\end{document}
![]() and variance
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b\sigma ^2/\mu ^{3}$$\end{document}
and variance
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b\sigma ^2/\mu ^{3}$$\end{document}
![]() .
.
Given a perceptual stimulus s and a set of decision choices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d^{\prime }\in \{1:d_{0}\}$$\end{document}
![]() , the neurons in the brain accumulate evidence in favor of the different alternatives. Modeling this behavior using latent Wiener processes
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$W_{d^{\prime },s}(\tau )$$\end{document}
, the neurons in the brain accumulate evidence in favor of the different alternatives. Modeling this behavior using latent Wiener processes
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$W_{d^{\prime },s}(\tau )$$\end{document}
![]() with unit variances, assuming that a decision d is made when the decision threshold
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d,s}$$\end{document}
with unit variances, assuming that a decision d is made when the decision threshold
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d,s}$$\end{document}
![]() for the dth option is crossed first, as illustrated in Fig. 1a, a probability model for the time
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d}$$\end{document}
for the dth option is crossed first, as illustrated in Fig. 1a, a probability model for the time
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d}$$\end{document}
![]() to reach decision d is obtained as
to reach decision d is obtained as
where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d,s}$$\end{document}
![]() denotes the rate of accumulation of evidence,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d,s}$$\end{document}
denotes the rate of accumulation of evidence,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d,s}$$\end{document}
![]() the decision boundaries, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\delta _{s}$$\end{document}
the decision boundaries, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\delta _{s}$$\end{document}
![]() an offset representing time not directly related to the underlying evidence accumulation processes (e.g., the time required to encode the sth signal before evidence accumulation begins, etc.). We let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\theta }_{d^{\prime },s}=(\delta _{s},\mu _{d^{\prime },s},b_{d^{\prime },s})^\textrm{T}$$\end{document}
an offset representing time not directly related to the underlying evidence accumulation processes (e.g., the time required to encode the sth signal before evidence accumulation begins, etc.). We let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\theta }_{d^{\prime },s}=(\delta _{s},\mu _{d^{\prime },s},b_{d^{\prime },s})^\textrm{T}$$\end{document}
![]() .
.
Joint model for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(d,\tau )$$\end{document}
![]() : Since a decision d is reached at response time
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau $$\end{document}
: Since a decision d is reached at response time
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau $$\end{document}
![]() if the corresponding threshold is crossed first, that is when
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\{\tau = \tau _{d}\} \cap _{d^{\prime } \ne d} \{\tau _{d^{\prime }} > \tau _{d}\}$$\end{document}
if the corresponding threshold is crossed first, that is when
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\{\tau = \tau _{d}\} \cap _{d^{\prime } \ne d} \{\tau _{d^{\prime }} > \tau _{d}\}$$\end{document}
![]() , we have
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d = \arg \min _{d^{\prime }\in \{1:d_{0}\}} \tau _{d^{\prime }}$$\end{document}
, we have
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d = \arg \min _{d^{\prime }\in \{1:d_{0}\}} \tau _{d^{\prime }}$$\end{document}
![]() . Assuming simultaneous accumulation of evidence for all decision categories, modeled by independent Wiener processes, and termination when the threshold for the observed decision category d is reached, the joint distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(d, \tau )$$\end{document}
. Assuming simultaneous accumulation of evidence for all decision categories, modeled by independent Wiener processes, and termination when the threshold for the observed decision category d is reached, the joint distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(d, \tau )$$\end{document}
![]() is thus given by
is thus given by
where, to distinguish from the generic notation f, we now use
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g(\cdot \mid {\theta })$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$G(\cdot \mid {\theta })$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$G(\cdot \mid {\theta })$$\end{document}
![]() to denote, respectively, the probability density function (pdf) and the cumulative distribution function (cdf) of an inverse Gaussian distribution, as defined in (1).
to denote, respectively, the probability density function (pdf) and the cumulative distribution function (cdf) of an inverse Gaussian distribution, as defined in (1).
Marginal model for
d: When the response times
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau $$\end{document}
![]() are unobserved, the probability of taking decision d given the stimulus s is thus obtained from (2) by integrating out the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau $$\end{document}
are unobserved, the probability of taking decision d given the stimulus s is thus obtained from (2) by integrating out the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau $$\end{document}
![]() as
as
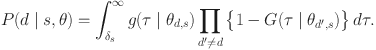
The construction of model (3) is similar to traditional multinomial probit/logit regression models except that the latent variables are now inverse Gaussian distributed as opposed to being normal or extreme-value distributed, and the observed category is associated with the minimum of the latent variables in contrast to being identified with the maximum of the latent variables. We thus refer to this model as a ‘multinomial inverse-probit model’.
With data on both response categories d and response times
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau $$\end{document}
![]() available, the joint model (2) was used to construct the likelihood function in Paulon et al. (Reference Paulon, Llanos, Chandrasekaran and Sarkar2021). In the absence of data on the response times
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau $$\end{document}
available, the joint model (2) was used to construct the likelihood function in Paulon et al. (Reference Paulon, Llanos, Chandrasekaran and Sarkar2021). In the absence of data on the response times
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau $$\end{document}
![]() , however, the inverse-probit model in (3) provides the basic building block for constructing the likelihood function for the observed response categories. As mentioned in the Abstract, discussed in the Introduction, and detailed in Sect. 2.1, the marginal inverse-probit model (3) for observed categories brings in many new identifiability issues and inference challenges not originally encountered for the joint model (2) developed in Paulon et al. (Reference Paulon, Llanos, Chandrasekaran and Sarkar2021). Solving these new challenges for the marginal model (3) to infer the underlying drift-diffusion parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\theta }_{d^{\prime },s}$$\end{document}
, however, the inverse-probit model in (3) provides the basic building block for constructing the likelihood function for the observed response categories. As mentioned in the Abstract, discussed in the Introduction, and detailed in Sect. 2.1, the marginal inverse-probit model (3) for observed categories brings in many new identifiability issues and inference challenges not originally encountered for the joint model (2) developed in Paulon et al. (Reference Paulon, Llanos, Chandrasekaran and Sarkar2021). Solving these new challenges for the marginal model (3) to infer the underlying drift-diffusion parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\theta }_{d^{\prime },s}$$\end{document}
![]() , for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d^{\prime }$$\end{document}
, for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d^{\prime }$$\end{document}
![]() , is the focus of this current article.
, is the focus of this current article.
2.1. Identifiability Issues and Related Modeling Challenges
To begin with, we note that model (3) in itself cannot be identified from data on only the response categories. The offset parameters can easily be seen to not be identifiable since
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$P\left( \tau _{d}\le \wedge _{d^{\prime }} \tau _{d^{\prime }}\right) =P\left\{ (\tau _{d}-\delta )\le \wedge _{d^{\prime }} \left( \tau _{d^{\prime }}-\delta \right) \right\} $$\end{document}
![]() for any
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\delta $$\end{document}
for any
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\delta $$\end{document}
![]() , where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\wedge _{d^{\prime }}\tau _{d^{\prime }}$$\end{document}
, where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\wedge _{d^{\prime }}\tau _{d^{\prime }}$$\end{document}
![]() denotes the minimum of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d^{\prime }}, d^{\prime }\in \{1:d_{0}\}$$\end{document}
denotes the minimum of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d^{\prime }}, d^{\prime }\in \{1:d_{0}\}$$\end{document}
![]() . As is also well known in the literature, in categorical probability models, the location and scale of the latent continuous variables are not also separately identifiable. The following lemma establishes these points for the inverse-probit model.
. As is also well known in the literature, in categorical probability models, the location and scale of the latent continuous variables are not also separately identifiable. The following lemma establishes these points for the inverse-probit model.
Lemma 1
The offset parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\delta _{s}$$\end{document}
![]() are not identifiable in model (3). The drift and the boundary parameters, respectively
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}$$\end{document}
are not identifiable in model (3). The drift and the boundary parameters, respectively
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d^{\prime },s}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d^{\prime },s}$$\end{document}
![]() , are also not separately identifiable in model (3).
, are also not separately identifiable in model (3).
In the proof of Lemma 1 given in Appendix A, we have specifically shown that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$ P\left( d\mid s, {\theta }\right) = P\left( d\mid s, {\theta }^{\star } \right) ,$$\end{document}
![]() where the drift and boundary parameters in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\theta }=\left\{ \left( \mu _{d^{\prime },s}, b_{d^{\prime },s}\right) ; d^{\prime }=1,\ldots , d_{0}\right\} $$\end{document}
where the drift and boundary parameters in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\theta }=\left\{ \left( \mu _{d^{\prime },s}, b_{d^{\prime },s}\right) ; d^{\prime }=1,\ldots , d_{0}\right\} $$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\theta }^{\star }=\left\{ \Big ( \mu _{d^{\prime },s}^{\star }, b_{d^{\prime },s}^{\star }\Big ); d^{\prime }=1,\ldots , d_{0}\right\} $$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\theta }^{\star }=\left\{ \Big ( \mu _{d^{\prime },s}^{\star }, b_{d^{\prime },s}^{\star }\Big ); d^{\prime }=1,\ldots , d_{0}\right\} $$\end{document}
![]() satisfy
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}^{\star }=c \mu _{d^{\prime },s}$$\end{document}
satisfy
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}^{\star }=c \mu _{d^{\prime },s}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d^{\prime },s}^{\star }= c^{-1} b_{d^{\prime },s}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d^{\prime },s}^{\star }= c^{-1} b_{d^{\prime },s}$$\end{document}
![]() for some constant
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$c>0$$\end{document}
for some constant
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$c>0$$\end{document}
![]() . The result follows by noting that the transformation
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d^{\prime },s}^{\star } = {c}^{-2}\tau _{d^{\prime },s}$$\end{document}
. The result follows by noting that the transformation
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d^{\prime },s}^{\star } = {c}^{-2}\tau _{d^{\prime },s}$$\end{document}
![]() does not change the ordering between the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d^{\prime },s}$$\end{document}
does not change the ordering between the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d^{\prime },s}$$\end{document}
![]() ’s and hence the probabilities of the resulting decisions
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d = \arg \min _{d^{\prime }\in \{1:d_{0}\}} \tau _{d^{\prime }} = \arg \min _{d^{\prime }\in \{1:d_{0}\}} \tau _{d^{\prime }}^{\star }$$\end{document}
’s and hence the probabilities of the resulting decisions
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d = \arg \min _{d^{\prime }\in \{1:d_{0}\}} \tau _{d^{\prime }} = \arg \min _{d^{\prime }\in \{1:d_{0}\}} \tau _{d^{\prime }}^{\star }$$\end{document}
![]() also remain the same. This has the simple implication that if the rate of accumulation of evidence is faster, then the same decision distribution is obtained if the corresponding boundaries are accordingly closer and conversely.
also remain the same. This has the simple implication that if the rate of accumulation of evidence is faster, then the same decision distribution is obtained if the corresponding boundaries are accordingly closer and conversely.
In fact, given the information on input and output categories alone, if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d_{0}$$\end{document}
![]() denotes the number of possible decision categories, at most
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d_{0}-1$$\end{document}
denotes the number of possible decision categories, at most
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d_{0}-1$$\end{document}
![]() parameters are estimable. To see this, consider the probabilities
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$P(d^{\prime } \mid s,{\theta })$$\end{document}
parameters are estimable. To see this, consider the probabilities
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$P(d^{\prime } \mid s,{\theta })$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d^{\prime }=1, \ldots , d_{0}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d^{\prime }=1, \ldots , d_{0}$$\end{document}
![]() , where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\theta }$$\end{document}
, where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\theta }$$\end{document}
![]() is the m-dimensional vector of parameters, possibly containing drift parameters and decision boundaries. Given the perceptual stimulus s as input, the probabilities satisfy
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sum _{d^{\prime }=1}^{d_{0}}P(d^{\prime } \mid s,{\theta })=1$$\end{document}
is the m-dimensional vector of parameters, possibly containing drift parameters and decision boundaries. Given the perceptual stimulus s as input, the probabilities satisfy
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sum _{d^{\prime }=1}^{d_{0}}P(d^{\prime } \mid s,{\theta })=1$$\end{document}
![]() . Thus, the function
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$P_{s}({\theta })= \{P(1 \mid s, {\theta }), \cdots , P(d_{0}\mid s, {\theta })\}^\textrm{T}$$\end{document}
. Thus, the function
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$P_{s}({\theta })= \{P(1 \mid s, {\theta }), \cdots , P(d_{0}\mid s, {\theta })\}^\textrm{T}$$\end{document}
![]() lie on a
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d_{0}-1$$\end{document}
lie on a
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d_{0}-1$$\end{document}
![]() -dimensional simplex,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$P_{s}({\theta }): {\theta }\rightarrow \Delta ^{d_{0}-1}$$\end{document}
-dimensional simplex,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$P_{s}({\theta }): {\theta }\rightarrow \Delta ^{d_{0}-1}$$\end{document}
![]() , and by the model in (3) the mapping is continuous. Thus, it can be shown by the Invariance of Domain theorem (see, e.g., Deo, Reference Deo2018) that if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$P_{s}$$\end{document}
, and by the model in (3) the mapping is continuous. Thus, it can be shown by the Invariance of Domain theorem (see, e.g., Deo, Reference Deo2018) that if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$P_{s}$$\end{document}
![]() is injective and continuous, then the domain of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$P_{s}$$\end{document}
is injective and continuous, then the domain of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$P_{s}$$\end{document}
![]() must belong to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mathbb {R}}^{m}$$\end{document}
must belong to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mathbb {R}}^{m}$$\end{document}
![]() , where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$m\le d_{0}-1$$\end{document}
, where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$m\le d_{0}-1$$\end{document}
![]() . Thus in order to ensure identifiabililty of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left\{ P_{s} ({\theta }); {\theta }\right\} $$\end{document}
. Thus in order to ensure identifiabililty of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left\{ P_{s} ({\theta }); {\theta }\right\} $$\end{document}
![]() , we must parametrize the probability vector with at most
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${d_{0}-1}$$\end{document}
, we must parametrize the probability vector with at most
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${d_{0}-1}$$\end{document}
![]() parameters.
parameters.
The existing literature on drift-diffusion models discussed in the Introduction has traditionally put more emphasis on modeling the drifts (as their reference in the literature as ‘drift’-diffusion models suggests). Previous research on joint models for response tones and associated response times in Paulon et al. (Reference Paulon, Llanos, Chandrasekaran and Sarkar2021) also suggest that the boundaries remain stable around a value of 2 and it is primarily the changes in the drift rates that explain longitudinal learning. In view of this, we keep the boundaries fixed at the constant
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b=2$$\end{document}
![]() and treat the drifts to be the free parameters instead. In our simulations and real data applications, it is observed that the estimates of the drift parameters and the associated cluster configurations are not very sensitive to small-to-moderate deviations of b around 2. In our codes implementing our method, available as part of the supplementary materials, we allow the practitioner to choose a value of b as they see fit for their specific application. The latent drift-diffusion process based with these constraints, namely
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\delta _{s} = 0$$\end{document}
and treat the drifts to be the free parameters instead. In our simulations and real data applications, it is observed that the estimates of the drift parameters and the associated cluster configurations are not very sensitive to small-to-moderate deviations of b around 2. In our codes implementing our method, available as part of the supplementary materials, we allow the practitioner to choose a value of b as they see fit for their specific application. The latent drift-diffusion process based with these constraints, namely
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\delta _{s} = 0$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d^{\prime },s} = b$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d^{\prime },s} = b$$\end{document}
![]() for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d^{\prime }$$\end{document}
for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d^{\prime }$$\end{document}
![]() , is shown in Fig. 1b.
, is shown in Fig. 1b.
While fixing
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\delta _{s}=0$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d^{\prime },s}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d^{\prime },s}$$\end{document}
![]() to some known constant b reduces the size of the parameter space to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d_{0}$$\end{document}
to some known constant b reduces the size of the parameter space to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d_{0}$$\end{document}
![]() , to ensure identifiability, we still need at least one more constraint on the drift parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
, to ensure identifiability, we still need at least one more constraint on the drift parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
![]() . In categorical probability models, the identifiabily problem of the location parameter is usually addressed by setting one category as a reference and modeling the probabilities of the others (Agresti, Reference Agresti2018; Albert & Chib, Reference Albert and Chib1993; Borooah, Reference Borooah2002; Chib & Greenberg, Reference Chib and Greenberg1998). However, posterior predictions from Bayesian categorical probability models with asymmetric constraints may be sensitive to the choice of reference category (see Burgette & Nordheim, Reference Burgette and Nordheim2012; Johndrow et al., Reference Johndrow, Dunson and Lum2013). Further, as also discussed in the Introduction, the goal of clustering the drift parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
. In categorical probability models, the identifiabily problem of the location parameter is usually addressed by setting one category as a reference and modeling the probabilities of the others (Agresti, Reference Agresti2018; Albert & Chib, Reference Albert and Chib1993; Borooah, Reference Borooah2002; Chib & Greenberg, Reference Chib and Greenberg1998). However, posterior predictions from Bayesian categorical probability models with asymmetric constraints may be sensitive to the choice of reference category (see Burgette & Nordheim, Reference Burgette and Nordheim2012; Johndrow et al., Reference Johndrow, Dunson and Lum2013). Further, as also discussed in the Introduction, the goal of clustering the drift parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
![]() across s can not be accomplished by this apparently simple solution.
across s can not be accomplished by this apparently simple solution.
The problem can be addressed by imposing a symmetric constraint on
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
![]() instead. A symmetric identifiability constraint has been previously proposed by Burgette et al. (Reference Burgette, Puelz and Hahn2021) in the context of multinomial probit models, where they considered a sum-to-zero constraint on the latent utilities. To implement the constraint, they introduced a faux base category indicator parameter, which is assigned a discrete uniform prior and then learned via MCMC. Given this faux base category indicator, the other parameters are adjusted so that the sum-to-zero restriction is satisfied. However, the introduction of a base category, even if adaptively chosen, does not facilitate the clustering of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
instead. A symmetric identifiability constraint has been previously proposed by Burgette et al. (Reference Burgette, Puelz and Hahn2021) in the context of multinomial probit models, where they considered a sum-to-zero constraint on the latent utilities. To implement the constraint, they introduced a faux base category indicator parameter, which is assigned a discrete uniform prior and then learned via MCMC. Given this faux base category indicator, the other parameters are adjusted so that the sum-to-zero restriction is satisfied. However, the introduction of a base category, even if adaptively chosen, does not facilitate the clustering of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
![]() within and across the different input categories s.
within and across the different input categories s.
2.2. Our Proposed Approach
In coming up with solutions for these challenges, we take into consideration the complex design of our motivating tone learning experiments, so that our approach is easily extendable to longitudinal mixed model settings, allowing us to (a) estimate the smoothly varying trajectories of the parameters as the participants learn over time, (b) accommodate the heterogeneity between the participants, and (c) compare between the estimates not just within but also crucially between the different panels.
Similar to the sum-to-zero constraint in the multinomial probit model of Burgette et al. (Reference Burgette, Puelz and Hahn2021), we impose a symmetric sum to a constant constraint on the drift parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
![]() to identify our new class of inverse-probit models, although our implementation is quite different from theirs. To conduct inference, we start with an unconstrained prior, then sample from the corresponding unconstrained posterior, and finally project these samples to the constrained space through a minimal distance mapping. Similar ideas have previously been applied to satisfy natural constraints in other contexts. See, e.g., Dunson and Neelon (Reference Dunson and Neelon2003) and Gunn and Dunson (Reference Gunn and Dunson2005).
to identify our new class of inverse-probit models, although our implementation is quite different from theirs. To conduct inference, we start with an unconstrained prior, then sample from the corresponding unconstrained posterior, and finally project these samples to the constrained space through a minimal distance mapping. Similar ideas have previously been applied to satisfy natural constraints in other contexts. See, e.g., Dunson and Neelon (Reference Dunson and Neelon2003) and Gunn and Dunson (Reference Gunn and Dunson2005).
This approach is significantly advantageous both from a modeling and a computational perspective. On one hand, the basic building blocks are relatively easily extended to complex longitudinal mixed model settings, on the other, posterior computation is facilitated as this allows the use of conjugate priors for the unconstrained parameters. Projection of the drift parameters onto the same space further makes them directly comparable, allowing clustering within and across the panels. The projected drifts can now be interpreted only on a relative scale but such compromises are not avoidable given the challenges we face.
2.2.1. Minimal Distance Mapping
As the drift parameters are positive, the sum to a constant k constraint leads to constrained space
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{k}=\{{\mu }: \textbf{1}^{T} {\mu }=k,\;\mu _{j}>0,\;j=1,\ldots ,d_{0}\}$$\end{document}
![]() on which
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
on which
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
![]() should be projected. The space
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{k}$$\end{document}
should be projected. The space
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{k}$$\end{document}
![]() is semi-closed, and therefore, the projection of any point
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }$$\end{document}
is semi-closed, and therefore, the projection of any point
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }$$\end{document}
![]() onto
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{k}$$\end{document}
onto
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{k}$$\end{document}
![]() may not exist. As a simple one dimensional example, let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$x=-1$$\end{document}
may not exist. As a simple one dimensional example, let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$x=-1$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mathcal {S}}=(0,1]$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mathcal {S}}=(0,1]$$\end{document}
![]() , then
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\arg \min _{y\in {\mathcal {S}}}|y-x|=0\notin {\mathcal {S}}$$\end{document}
, then
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\arg \min _{y\in {\mathcal {S}}}|y-x|=0\notin {\mathcal {S}}$$\end{document}
![]() . Further, from a practical perspective, a drift parameter infinitesimally close to zero makes the distribution of the associated response times very flat which is typically not observed in real data. Therefore, we choose a small
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varepsilon >0$$\end{document}
. Further, from a practical perspective, a drift parameter infinitesimally close to zero makes the distribution of the associated response times very flat which is typically not observed in real data. Therefore, we choose a small
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varepsilon >0$$\end{document}
![]() and project
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }$$\end{document}
and project
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }$$\end{document}
![]() onto
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$ \mathcal{S}_{\varepsilon , k}=\{{\mu }: \textbf{1}^{T} {\mu }=k,\;\mu _{j}\ge \varepsilon ,\;j=1,\ldots ,d_{0}\}.$$\end{document}
onto
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$ \mathcal{S}_{\varepsilon , k}=\{{\mu }: \textbf{1}^{T} {\mu }=k,\;\mu _{j}\ge \varepsilon ,\;j=1,\ldots ,d_{0}\}.$$\end{document}
![]() We then define the projection of a point
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }$$\end{document}
We then define the projection of a point
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }$$\end{document}
![]() onto
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{\varepsilon ,k}$$\end{document}
onto
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{\varepsilon ,k}$$\end{document}
![]() through minimal distance mapping as
through minimal distance mapping as
where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Vert \cdot \Vert $$\end{document}
![]() is the Euclidean norm. Note that for appropriate choices of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(k,\varepsilon )$$\end{document}
is the Euclidean norm. Note that for appropriate choices of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(k,\varepsilon )$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{\varepsilon ,k}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{\varepsilon ,k}$$\end{document}
![]() is non-empty, closed and convex. Therefore,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }^{\star }$$\end{document}
is non-empty, closed and convex. Therefore,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }^{\star }$$\end{document}
![]() exists and is unique by the Hilbert projection theorem (Rudin, Reference Rudin1991). The solution to this projection problem comes from the following result from Beck (Reference Beck2017).
exists and is unique by the Hilbert projection theorem (Rudin, Reference Rudin1991). The solution to this projection problem comes from the following result from Beck (Reference Beck2017).
Lemma 2
Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$ \mathcal{S}_{\varepsilon , k}$$\end{document}
![]() be as defined above, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{\varepsilon }=\left\{ {\mu }: \mu _{j}\ge \varepsilon ,\;j=1,\ldots ,d_{0} \right\} $$\end{document}
be as defined above, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{\varepsilon }=\left\{ {\mu }: \mu _{j}\ge \varepsilon ,\;j=1,\ldots ,d_{0} \right\} $$\end{document}
![]() . Then,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textrm{Proj}_{ \mathcal{S}_{\varepsilon , k}}({\mu })=\textrm{Proj}_{ \mathcal{S}_{\varepsilon }}({\mu }- u^{\star } \textbf{1})$$\end{document}
. Then,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textrm{Proj}_{ \mathcal{S}_{\varepsilon , k}}({\mu })=\textrm{Proj}_{ \mathcal{S}_{\varepsilon }}({\mu }- u^{\star } \textbf{1})$$\end{document}
![]() , where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$u^{\star }$$\end{document}
, where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$u^{\star }$$\end{document}
![]() is a solution to the equation
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$ \textbf{1}^{T} \textrm{Proj}_{ \mathcal{S}_{\varepsilon }}({\mu }- u^{\star } \textbf{1})=k $$\end{document}
is a solution to the equation
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$ \textbf{1}^{T} \textrm{Proj}_{ \mathcal{S}_{\varepsilon }}({\mu }- u^{\star } \textbf{1})=k $$\end{document}
![]() .
.
Although the analytical form of the solution is not available, as is evident from the above result, the solution mainly relies on finding a root
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$u^{\star }$$\end{document}
![]() of the non-increasing function
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\phi (u^{\star })=\textbf{1}^{T} \textrm{Proj}_{ \mathcal{S}_{\varepsilon }}({\mu }- u^{\star } \textbf{1})-k$$\end{document}
of the non-increasing function
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\phi (u^{\star })=\textbf{1}^{T} \textrm{Proj}_{ \mathcal{S}_{\varepsilon }}({\mu }- u^{\star } \textbf{1})-k$$\end{document}
![]() . We apply an algorithm based on Duchi et al. (Reference Duchi, Shalev-Shwartz, Singer and Chandra2008) to reach the solution. The algorithm is described in “Appendix C”.
. We apply an algorithm based on Duchi et al. (Reference Duchi, Shalev-Shwartz, Singer and Chandra2008) to reach the solution. The algorithm is described in “Appendix C”.
2.2.2. Identifiability Restrictions
The projection approach solves the problem of identifiability and maps the probability vector corresponding to an input tone s to the constraint space of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{\varepsilon ,k}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{\varepsilon ,k}$$\end{document}
![]() . The following theorem shows that the mapping from the constrained space of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
. The following theorem shows that the mapping from the constrained space of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
![]() to the probability vector
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\textbf{P}}}({\mu }_{1:d_{0},s})=\{p_{1}({\mu }_{1:d_{0},s}), \dots , p_{d_{0}}({\mu }_{1:d_{0},s}) \}^\textrm{T}$$\end{document}
to the probability vector
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\textbf{P}}}({\mu }_{1:d_{0},s})=\{p_{1}({\mu }_{1:d_{0},s}), \dots , p_{d_{0}}({\mu }_{1:d_{0},s}) \}^\textrm{T}$$\end{document}
![]() is injective. To keep the ideas simple, we consider the domain of the function to be
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{0,k}$$\end{document}
is injective. To keep the ideas simple, we consider the domain of the function to be
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{0,k}$$\end{document}
![]() (i.e.,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varepsilon =0$$\end{document}
(i.e.,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varepsilon =0$$\end{document}
![]() ) instead of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{\varepsilon ,k}$$\end{document}
) instead of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{\varepsilon ,k}$$\end{document}
![]() although a very similar proof would follow if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{\varepsilon ,k}$$\end{document}
although a very similar proof would follow if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{\varepsilon ,k}$$\end{document}
![]() were considered.
were considered.
Theorem 1
Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$p_{d}({\mu }_{1:d_{0},s})$$\end{document}
![]() be the probability of observing the output tone d given the input tone s and the drift parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
be the probability of observing the output tone d given the input tone s and the drift parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
![]() , as given in (3), for each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1:d_{0}$$\end{document}
, as given in (3), for each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1:d_{0}$$\end{document}
![]() . Suppose
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
. Suppose
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
![]() lies on the space
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{0,k}$$\end{document}
lies on the space
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{0,k}$$\end{document}
![]() . Then, the function from
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{0,k}$$\end{document}
. Then, the function from
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{0,k}$$\end{document}
![]() to the space of probabilities
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left\{ p_{d}({\mu }_{1:d_{0},s}); d=1:d_{0}\right\} $$\end{document}
to the space of probabilities
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left\{ p_{d}({\mu }_{1:d_{0},s}); d=1:d_{0}\right\} $$\end{document}
![]() is injective.
is injective.
A proof is presented in “Appendix B”.
2.3.3. Conjugate Priors for the Unconstrained Drifts
From (3), given
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{1},\ldots ,\tau _{d_{0}}$$\end{document}
![]() , such that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d}\le \min \left\{ \tau _{1},\ldots ,\tau _{d_{0}} \right\} $$\end{document}
, such that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d}\le \min \left\{ \tau _{1},\ldots ,\tau _{d_{0}} \right\} $$\end{document}
![]() , the posterior full conditional of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
, the posterior full conditional of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
![]() is proportional to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\pi _{{\mu }}^{(n)} \propto \pi ( {\mu }_{1:d_{0},s} ) \times \prod _{d^{\prime }=1}^{d_{0}} g\left( \tau _{d^{\prime }} ~ \mid \mu _{d^{\prime },s}\right) ,$$\end{document}
is proportional to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\pi _{{\mu }}^{(n)} \propto \pi ( {\mu }_{1:d_{0},s} ) \times \prod _{d^{\prime }=1}^{d_{0}} g\left( \tau _{d^{\prime }} ~ \mid \mu _{d^{\prime },s}\right) ,$$\end{document}
![]() where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\pi (\cdot )$$\end{document}
where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\pi (\cdot )$$\end{document}
![]() is the prior of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
is the prior of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
![]() . Observe that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\prod _{d^{\prime }=1}^{d_{0}} g\left( \tau _{d^{\prime }} ~ \mid \mu _{d^{\prime },s}\right) $$\end{document}
. Observe that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\prod _{d^{\prime }=1}^{d_{0}} g\left( \tau _{d^{\prime }} ~ \mid \mu _{d^{\prime },s}\right) $$\end{document}
![]() is Gaussian in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
is Gaussian in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
![]() . A Gaussian prior on
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
. A Gaussian prior on
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
![]() thus induces a conditional posterior for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
thus induces a conditional posterior for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
![]() that is also Gaussian and hence very easy to sample from. Importantly, these benefits also extend naturally to multivariate Gaussian priors for any parameter vector
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\beta }_{d^{\prime },s}$$\end{document}
that is also Gaussian and hence very easy to sample from. Importantly, these benefits also extend naturally to multivariate Gaussian priors for any parameter vector
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\beta }_{d^{\prime },s}$$\end{document}
![]() that relates to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}$$\end{document}
that relates to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}$$\end{document}
![]() linearly. This will be crucial in allowing us to extend the basic building block to longitudinal functional mixed model settings in Sect. 3 next, where we will be modeling time-varying
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}(t)$$\end{document}
linearly. This will be crucial in allowing us to extend the basic building block to longitudinal functional mixed model settings in Sect. 3 next, where we will be modeling time-varying
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}(t)$$\end{document}
![]() as flexible mixtures of B-splines with associated coefficients
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\beta }_{d^{\prime },s}$$\end{document}
as flexible mixtures of B-splines with associated coefficients
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\beta }_{d^{\prime },s}$$\end{document}
![]() .
.
2.2.4. Justification as a Proper Bayesian Procedure
Define the constrained conditional posterior distribution,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\tilde{\pi }}_{{\tilde{{\mu }}}}^{(n)}$$\end{document}
![]() , of the drift parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }$$\end{document}
, of the drift parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }$$\end{document}
![]() as
as
where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\pi _{{\mu }}^{(n)}$$\end{document}
![]() is the unconstrained conditional posterior of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
is the unconstrained conditional posterior of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}$$\end{document}
![]() , given the other variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\zeta }$$\end{document}
, given the other variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\zeta }$$\end{document}
![]() . The analytic form of the constrained conditional posterior is not available.
. The analytic form of the constrained conditional posterior is not available.
Sen et al. (Reference Sen, Patra and Dunson2018) established a proper Bayesian justification for the posterior projection approach by showing the existence of a prior
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\tilde{\pi }}\left( {\mu }_{1:d_{0},s}\right) $$\end{document}
![]() on the constrained space
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{\varepsilon ,k}$$\end{document}
on the constrained space
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{\varepsilon ,k}$$\end{document}
![]() such that the resulting posterior is the same as the projected posterior
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\tilde{\pi }}_{{\tilde{{\mu }}}}^{(n)}$$\end{document}
such that the resulting posterior is the same as the projected posterior
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\tilde{\pi }}_{{\tilde{{\mu }}}}^{(n)}$$\end{document}
![]() . When
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{\varepsilon ,k}$$\end{document}
. When
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{\varepsilon ,k}$$\end{document}
![]() is non-empty, closed, and convex, i.e., the projection operator is measurable, such a prior exists if the unconstrained posterior is absolutely continuous with respect to the unconstrained prior (Sen et al., Reference Sen, Patra and Dunson2018, Corollary 1). As the unconstrained induced prior and posterior of the drift parameters are both Gaussian, this result holds in our case as well.
is non-empty, closed, and convex, i.e., the projection operator is measurable, such a prior exists if the unconstrained posterior is absolutely continuous with respect to the unconstrained prior (Sen et al., Reference Sen, Patra and Dunson2018, Corollary 1). As the unconstrained induced prior and posterior of the drift parameters are both Gaussian, this result holds in our case as well.
3. Extension to Longitudinal Mixed Models
In this section we adapt the inverse-probit model discussed in Sect. 2 to complex longitudinal design of our motivating PTC1 data set described in the Introduction. Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$s_{i,\ell ,t}$$\end{document}
![]() denote the input tone for the ith individual in the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\ell $$\end{document}
denote the input tone for the ith individual in the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\ell $$\end{document}
![]() th trial of block t. Likewise, let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d_{i,\ell ,t}$$\end{document}
th trial of block t. Likewise, let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d_{i,\ell ,t}$$\end{document}
![]() denote, respectively, the output tone selected by the ith individual in the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\ell $$\end{document}
denote, respectively, the output tone selected by the ith individual in the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\ell $$\end{document}
![]() th trial of block t. Setting the offsets at zero, and boundary parameters to a fixed constant b, we now have
th trial of block t. Setting the offsets at zero, and boundary parameters to a fixed constant b, we now have
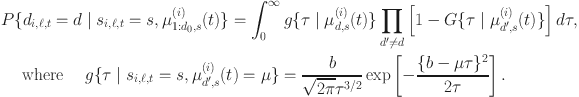
The drift rates
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}^{(i)}(t)$$\end{document}
![]() now vary with the blocks t. In addition, we accommodate random effects by allowing
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}^{(i)}(t)$$\end{document}
now vary with the blocks t. In addition, we accommodate random effects by allowing
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}^{(i)}(t)$$\end{document}
![]() to also depend on the subject index i. We let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\textbf{d}}}=\{d_{i,\ell ,t}\}_{i,\ell ,t}$$\end{document}
to also depend on the subject index i. We let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\textbf{d}}}=\{d_{i,\ell ,t}\}_{i,\ell ,t}$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d_{0}$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d_{0}$$\end{document}
![]() be the number of possible decision categories (T1, T2,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\ldots $$\end{document}
be the number of possible decision categories (T1, T2,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\ldots $$\end{document}
![]() , T
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${d_{0}}$$\end{document}
, T
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${d_{0}}$$\end{document}
![]() ). The likelihood function thus takes the form
). The likelihood function thus takes the form
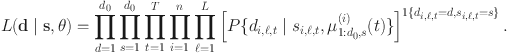
We reiterate that in deriving the identifiability conditions and designing their implementation strategy in Sect. 2.2, we had to make sure that they would be applicable to the complex multi-subject longitudinal design of the PTC1 data set. Following those ideas, we model the time-varying mixed effects drift parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}^{(i)}(t)$$\end{document}
![]() without any constraints first, then project them to the space satisfying the necessary identifying conditions.
without any constraints first, then project them to the space satisfying the necessary identifying conditions.
For the unconstrained model, we follow the outline of Paulon et al. (Reference Paulon, Llanos, Chandrasekaran and Sarkar2021) with necessary likelihood adjustments. The details are deferred to Section S.1 of the supplementary material. We present here a general outline.
We decompose
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}^{(i)}(t) = f_{d^{\prime },s}(t) + u_{d^{\prime },s}^{(i)}(t)$$\end{document}
![]() where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$f_{d^{\prime },s}(t)$$\end{document}
where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$f_{d^{\prime },s}(t)$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$u_{d^{\prime },s}^{(i)}(t)$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$u_{d^{\prime },s}^{(i)}(t)$$\end{document}
![]() denote, respectively, fixed and random effects components, which are both modeled using flexible mixtures of B-spline bases. This allows us to cluster the fixed effects for different
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(d^{\prime },s)$$\end{document}
denote, respectively, fixed and random effects components, which are both modeled using flexible mixtures of B-spline bases. This allows us to cluster the fixed effects for different
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(d^{\prime },s)$$\end{document}
![]() combinations with similar shapes by clustering the corresponding B-spline coefficients.
combinations with similar shapes by clustering the corresponding B-spline coefficients.
Given posterior samples of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$f_{d^{\prime },s}(t)$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$u_{d^{\prime },s}^{(i)}(t)$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$u_{d^{\prime },s}^{(i)}(t)$$\end{document}
![]() , unconstrained samples of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}^{(i)}(t)$$\end{document}
, unconstrained samples of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}^{(i)}(t)$$\end{document}
![]() are obtained. For every input tone s, these unconstrained
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}^{(i)}(t)$$\end{document}
are obtained. For every input tone s, these unconstrained
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s}^{(i)}(t)$$\end{document}
![]() ’s are then projected to the space
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{\varepsilon ,k}$$\end{document}
’s are then projected to the space
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{\varepsilon ,k}$$\end{document}
![]() following the method described in Sect. 2.2.1.
following the method described in Sect. 2.2.1.
4. Posterior Inference
Posterior inference for our proposed inverse-probit mixed model is carried out using samples drawn from the posterior using MCMC algorithm. The algorithm carefully exploits the conditional independence relationships encoded in the model as well as the latent variable construction of the model.
Inference can be greatly simplified by sampling the passage times
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{1:d_{0}}$$\end{document}
![]() and then conditioning on them. However, it is not possible to generate
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{1:d_{0}}$$\end{document}
and then conditioning on them. However, it is not possible to generate
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{1:d_{0}}$$\end{document}
![]() sequentially, e.g., by generating the passage time of the d-th decision choice
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d}$$\end{document}
sequentially, e.g., by generating the passage time of the d-th decision choice
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d}$$\end{document}
![]() independently, and that of the other decision choices from a truncated inverse-Gaussian distribution, left truncated at
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d}$$\end{document}
independently, and that of the other decision choices from a truncated inverse-Gaussian distribution, left truncated at
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d}$$\end{document}
![]() .Footnote 1
.Footnote 1
We implement a simple accept-reject sampler instead which generates values from the joint distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{1:d_{0}}$$\end{document}
![]() and accepts the sample if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d}\le \tau _{1:d_{0}}$$\end{document}
and accepts the sample if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d}\le \tau _{1:d_{0}}$$\end{document}
![]() . It is fast and produces a sample from the desired target conditional distribution. We formalize this result in the following lemma.
. It is fast and produces a sample from the desired target conditional distribution. We formalize this result in the following lemma.
Lemma 3
Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g\left( \tau _{1:d_{0}}\mid \mu _{1:d_{0}} \right) $$\end{document}
![]() be the joint distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{1:d_{0}}$$\end{document}
be the joint distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{1:d_{0}}$$\end{document}
![]() . Consider the following accept-reject algorithm:
. Consider the following accept-reject algorithm:
Algorithm 1 Generating the passage times
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{1:d_{0}}$$\end{document}
![]() given
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\arg \min _{d^{\prime }\in \{1:d_{0}\}}\tau _{d^{\prime }}=d$$\end{document}
given
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\arg \min _{d^{\prime }\in \{1:d_{0}\}}\tau _{d^{\prime }}=d$$\end{document}
![]()
Algorithm 1 generates samples from the conditional joint distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{1:d_{0}}$$\end{document}
![]() , conditioned on the event
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d}\le \tau _{1:d_{0}}$$\end{document}
, conditioned on the event
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d}\le \tau _{1:d_{0}}$$\end{document}
![]() .
.
Proof of Lemma 3 is provided in “Appendix D”.
It can be verified that the acceptance ratio of Algorithm 1 is
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M^{-1}=P\left( \tau _{d} \le \tau _{1:d_{0}}\right) $$\end{document}
![]() (see Robert & Casella, Reference Robert and Casella2004) which depends on the drift parameters only. If the drift parameters are ordered accordingly, so as to satisfy
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d} \ge \mu _{1:d_{0}}$$\end{document}
(see Robert & Casella, Reference Robert and Casella2004) which depends on the drift parameters only. If the drift parameters are ordered accordingly, so as to satisfy
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d} \ge \mu _{1:d_{0}}$$\end{document}
![]() , the acceptance ratios increase. The algorithm thus becomes faster as the sampler converges.
, the acceptance ratios increase. The algorithm thus becomes faster as the sampler converges.
As noted earlier, sampling the latent inverse-gaussian distributed response times
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{1:d_{0}}$$\end{document}
![]() greatly simplifies computation. Most of the chosen priors, including the priors on the coefficients
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\beta }$$\end{document}
greatly simplifies computation. Most of the chosen priors, including the priors on the coefficients
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\beta }$$\end{document}
![]() in the fixed and random effects, are conjugate. Due to space constraints, the details are deferred to Section S.3 in the supplementary material.
in the fixed and random effects, are conjugate. Due to space constraints, the details are deferred to Section S.3 in the supplementary material.
5. Simulation Studies
In this section, we discuss the results of a synthetic numerical experiment. We simulate data from a complex longitudinal design that mimics the real PTC1 data set. Our generating model contains fixed effects components attributed to different input-response tone combinations and random components attributed to individuals.
We recall that our main objective here is to identify the similarities and differences between the underlying brain mechanisms associated with different input-response category combinations over time while also assessing their individual heterogeneity, as characterized by latent drift-diffusion processes whose parameters can be biologically interpreted. The estimation of the probability curves for different input-response combinations, while a good indicator of our model’s fit, is not the main purpose of this endeavor. Traditional categorical probability models, such as multinomial probit or logit, are thus not relevant to the scientific problem we are trying to address here. We are also not aware of any other work in the drift-diffusion literature that attempts to estimate the underlying parameters from category response data alone. In view of this, we restrict our focus to evaluating the performance of the proposed biologically meaningful longitudinal inverse-probit mixed model but do not present comparisons with any other model.
Design In designing the simulation scenario, we have tried to mimic our motivating category learning data sets. We chose
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$n=20$$\end{document}
![]() as the number of participants being trained over
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T=10$$\end{document}
as the number of participants being trained over
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T=10$$\end{document}
![]() blocks to identify
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d_{0}=4$$\end{document}
blocks to identify
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d_{0}=4$$\end{document}
![]() tones. For each input tone and each block, there are
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$L=40$$\end{document}
tones. For each input tone and each block, there are
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$L=40$$\end{document}
![]() trials. We set the true
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}(t)$$\end{document}
trials. We set the true
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}(t)$$\end{document}
![]() values in such a way that they are far from satisfying the constraint
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sum _{d^{\prime } =1:d_{0}}\mu _{d^{\prime },s}=k$$\end{document}
values in such a way that they are far from satisfying the constraint
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sum _{d^{\prime } =1:d_{0}}\mu _{d^{\prime },s}=k$$\end{document}
![]() , and the decision boundary is set to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b=2$$\end{document}
, and the decision boundary is set to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b=2$$\end{document}
![]() for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(d^{\prime },s)$$\end{document}
for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(d^{\prime },s)$$\end{document}
![]() . The true drift parameters and the true probabilities, averaged over the participants of each input-response category combination, are shown in Fig. 3.
. The true drift parameters and the true probabilities, averaged over the participants of each input-response category combination, are shown in Fig. 3.
There are four true clusters in total, two for correct categorizations,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{1}, S_{2}$$\end{document}
![]() , and two for incorrect categorizations,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{1}, M_{2}$$\end{document}
, and two for incorrect categorizations,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{1}, M_{2}$$\end{document}
![]() , as follows:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{1}=\{(1,1),(2,2)\}$$\end{document}
, as follows:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{1}=\{(1,1),(2,2)\}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{2}=\{(3,3),(4,4)\}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{2}=\{(3,3),(4,4)\}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{1}=\{(1,2),(1,3),(2,1),(2,3),(3,4),(4,3)\}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{1}=\{(1,2),(1,3),(2,1),(2,3),(3,4),(4,3)\}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{2}=\{(1,4),(2,4),(3,1),(3,2),(4,1),(4,2)\}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{2}=\{(1,4),(2,4),(3,1),(3,2),(4,1),(4,2)\}$$\end{document}
![]() . We may interpret
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{1}$$\end{document}
. We may interpret
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{1}$$\end{document}
![]() as the cluster of difficult alternatives, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{2}$$\end{document}
as the cluster of difficult alternatives, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{2}$$\end{document}
![]() as the cluster of easy alternatives. Thus, there are similarities in overall trajectories of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\{T_{1},T_{2}\}$$\end{document}
as the cluster of easy alternatives. Thus, there are similarities in overall trajectories of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\{T_{1},T_{2}\}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\{T_{3},T_{4}\}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\{T_{3},T_{4}\}$$\end{document}
![]() , differentiating between easy and hard category recognition problems. We experimented with 50 synthetic data sets generated according to this design.
, differentiating between easy and hard category recognition problems. We experimented with 50 synthetic data sets generated according to this design.
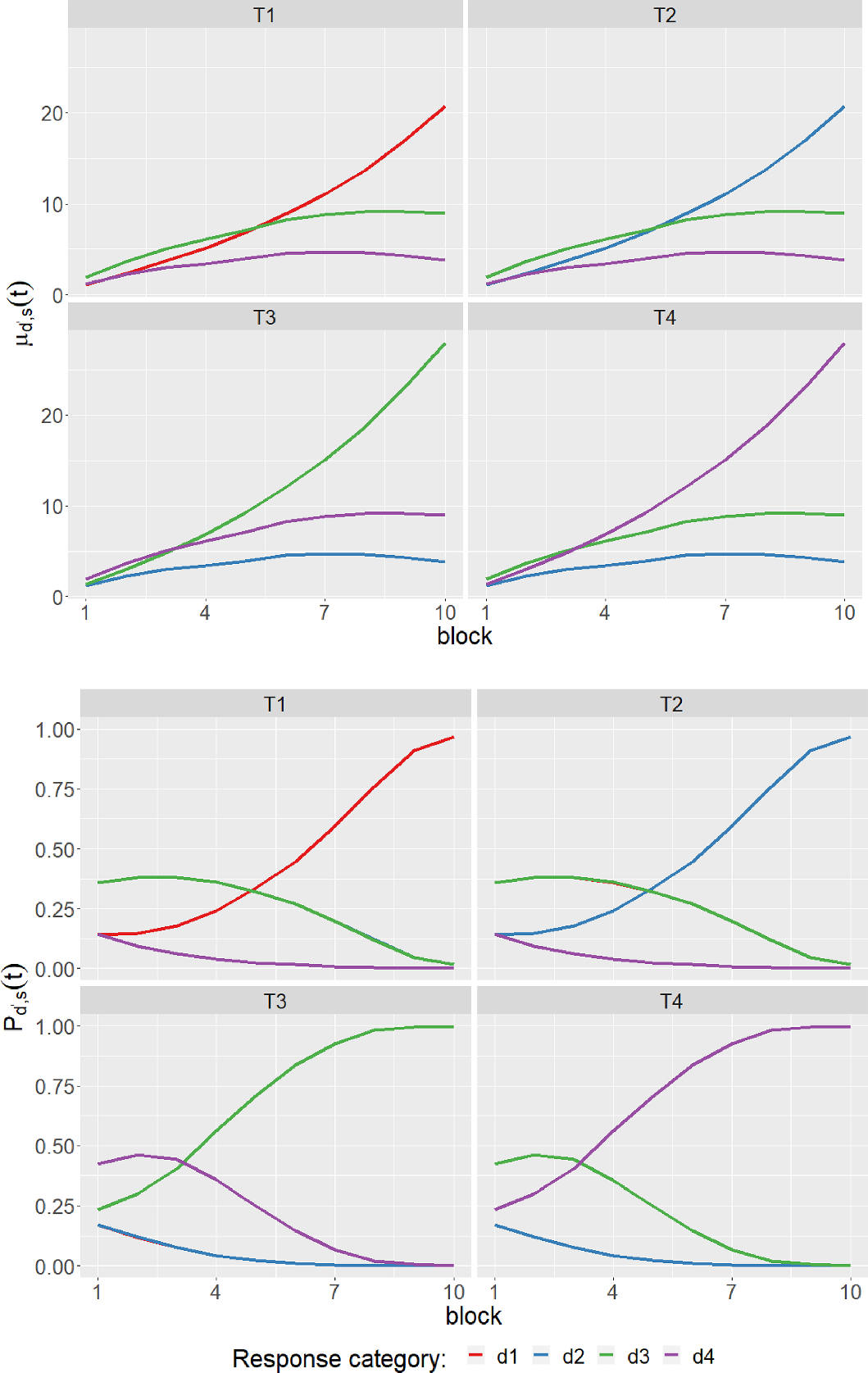
Figure 3 Description of the synthetic data: True values of the drift parameters averaged over the subjects, denoted by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}(t)$$\end{document}
![]() , and true probabilities
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$P\{d_{i,\ell ,t} \mid s_{i,\ell ,t}, {\mu }_{1:d_{0},s}^{(i)}(t)\}$$\end{document}
, and true probabilities
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$P\{d_{i,\ell ,t} \mid s_{i,\ell ,t}, {\mu }_{1:d_{0},s}^{(i)}(t)\}$$\end{document}
![]() averaged over the subjects, denoted here by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$P_{d^{\prime },s}(t)$$\end{document}
averaged over the subjects, denoted here by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$P_{d^{\prime },s}(t)$$\end{document}
![]() . Here T1, T2, T3, and T4 represent input categories 1 to 4, respectively. Some of the curves overlap according to the true clustering structure described in Sect. 5.
. Here T1, T2, T3, and T4 represent input categories 1 to 4, respectively. Some of the curves overlap according to the true clustering structure described in Sect. 5.
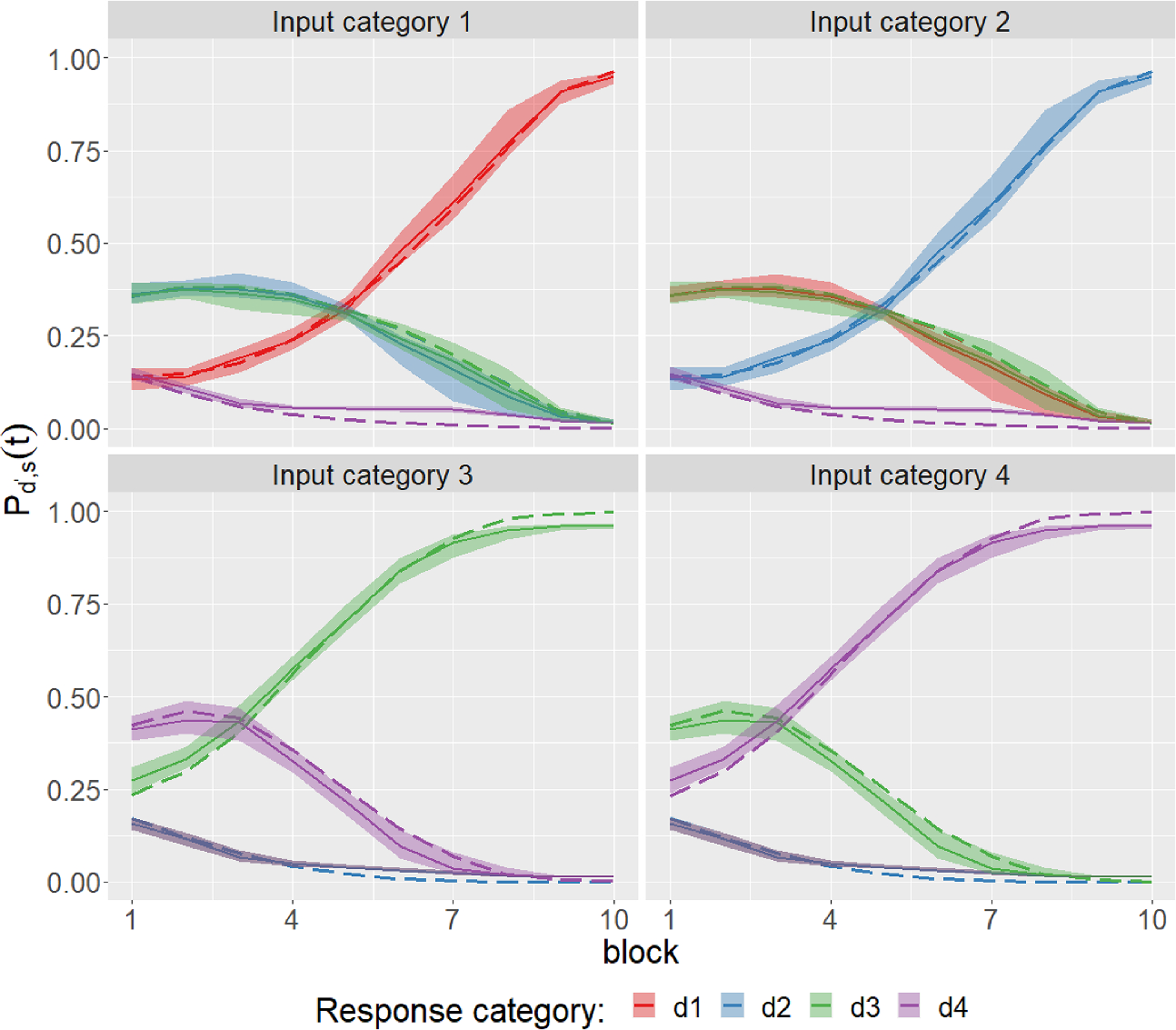
Figure 4 Results for synthetic data: Posterior trajectories of the probabilities for each combination of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(d^{\prime },s)$$\end{document}
![]() over blocks estimated by the proposed model. The shaded areas represent the corresponding 95% point-wise credible intervals. The thick dashed lines represent underlying true curves some of which overlap according to the true clustering structure described in Sect. 5.
over blocks estimated by the proposed model. The shaded areas represent the corresponding 95% point-wise credible intervals. The thick dashed lines represent underlying true curves some of which overlap according to the true clustering structure described in Sect. 5.
Results As the true drift parameters themselves do not satisfy the constraint, and the estimated drift parameters are on the constrained space, we cannot validate our method by its predictive performance of the drift parameters. Instead, the proposed method is validated in terms of the estimated probabilities.
Figure 4 shows the estimated posterior probability trajectories along with the 95% credible interval and the underlying true probability curves for every combination
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(d^{\prime },s)$$\end{document}
![]() in a typical scenario. The credible interval fails to capture the truth in two situations, when the true probability is very close to zero, or it is very close to one. The former case corresponds to classes with very low success probability, resulting in very few observations to estimate. The latter is underestimated as a consequence of the former since the probabilities add up to one.
in a typical scenario. The credible interval fails to capture the truth in two situations, when the true probability is very close to zero, or it is very close to one. The former case corresponds to classes with very low success probability, resulting in very few observations to estimate. The latter is underestimated as a consequence of the former since the probabilities add up to one.
The results produced by our method are mostly stable and consistent across all synthetic data sets. There are, however, a few cases of incorrect cluster assignments, resulting in some outliers in each boxplot. Note that if an incorrect cluster assignment takes place, the probabilities of all input-response combinations are affected by that. For example, if a component of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$ M_{1}$$\end{document}
![]() is wrongly assigned to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{2}$$\end{document}
is wrongly assigned to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{2}$$\end{document}
![]() , then not only the probabilities of input–output combinations in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{1}$$\end{document}
, then not only the probabilities of input–output combinations in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{1}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{2}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{2}$$\end{document}
![]() are affected, since the probabilities add up to one, those of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{1}$$\end{document}
are affected, since the probabilities add up to one, those of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{1}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{2}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{2}$$\end{document}
![]() are also affected.
are also affected.
In estimating the probabilities, the overall mean squared error, i.e., the mean squared difference of the estimated and the true probabilities taking all combinations of (d, s, i, t) into account, came out to be 0.0028. Figure 5 provides a detailed description of the estimation of the probabilities for two input categories (one from each similarity group). As described for the individual simulation results, there are cases of under-estimation of the probabilities which are close to one, and consequently, over-estimation of the probabilities close to zero. However, the amount of departure from the true probability in each case is very small which can also be seen in the small overall MSE.
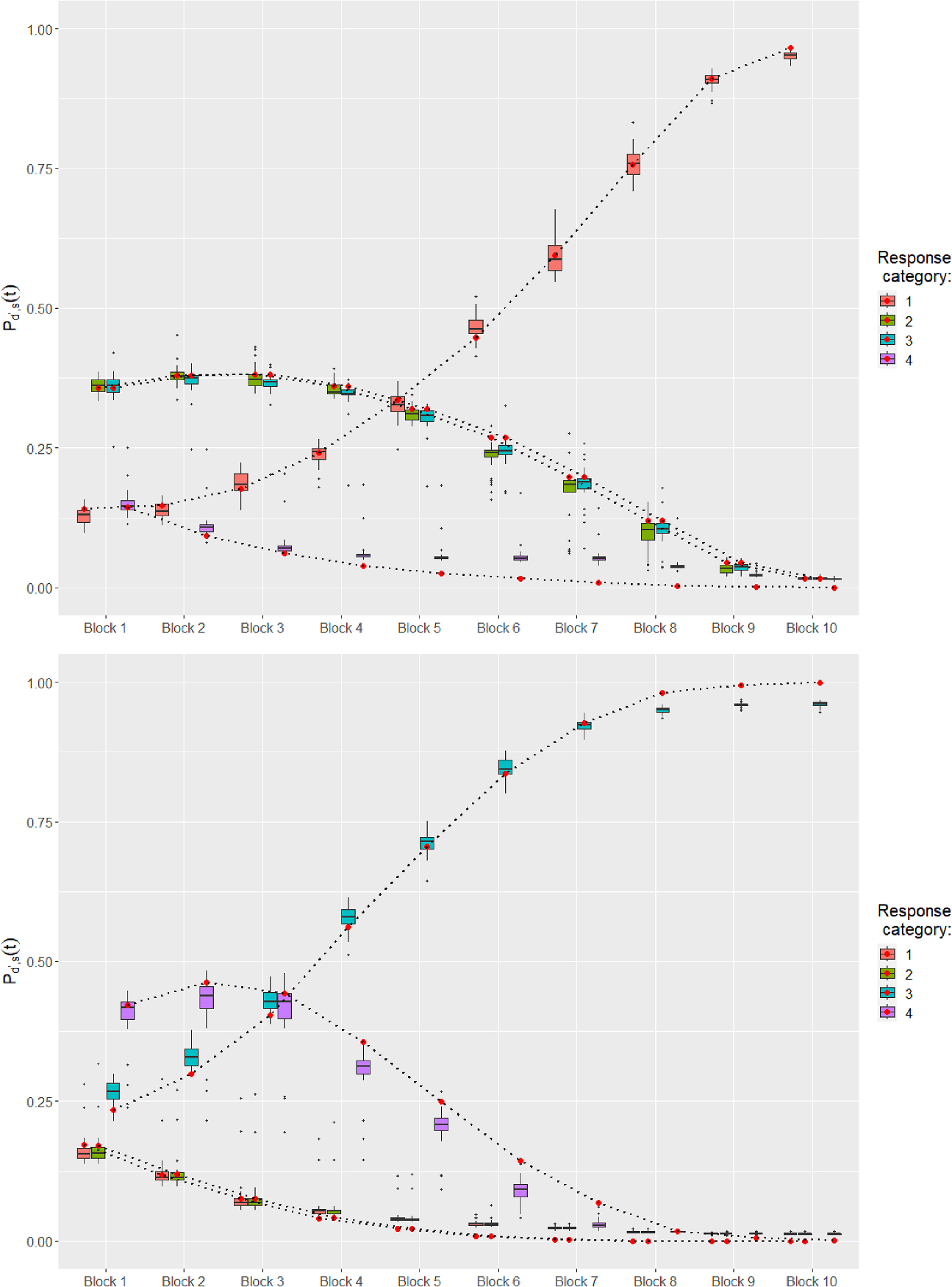
Figure 5 Results of the synthetic data: Boxplots of the estimated probabilities over 50 simulations, and true probabilities (in red dot) of each block and for two panels, one from each similarity group (panel
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{1}$$\end{document}
![]() in the top and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{3}$$\end{document}
in the top and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{3}$$\end{document}
![]() in the bottom).
in the bottom).
Further, the overall efficiency in identifying the true clustering structure is validated using Rand (Rand, Reference Rand1971) and adjusted Rand (Hubert & Arabie, Reference Hubert and Arabie1985) indices. The definitions of Rand and adjusted Rand indices are provided in Section S.6 in the supplementary material. The average Rand and adjusted Rand indices for our proposed method over 50 simulations 0.9105 and 0.8277, respectively, indicating high overall efficacy in correctly clustering the probability curves.
6. Applications
Analysis of the PTC1 Data Set We present here the analysis of the PTC1 data set described in Sect. 1 using our proposed longitudinal inverse-probit mixed model. We first demonstrate the performance of the proposed method in estimating the probabilities associated with different (d, s) pairs. Figure 6 shows the 95% credible intervals for the estimated probabilities for different input tones, along with the average proportions of times an input tone was classified into different tone categories across subjects. The latter serves as the empirical estimate of the probabilities.
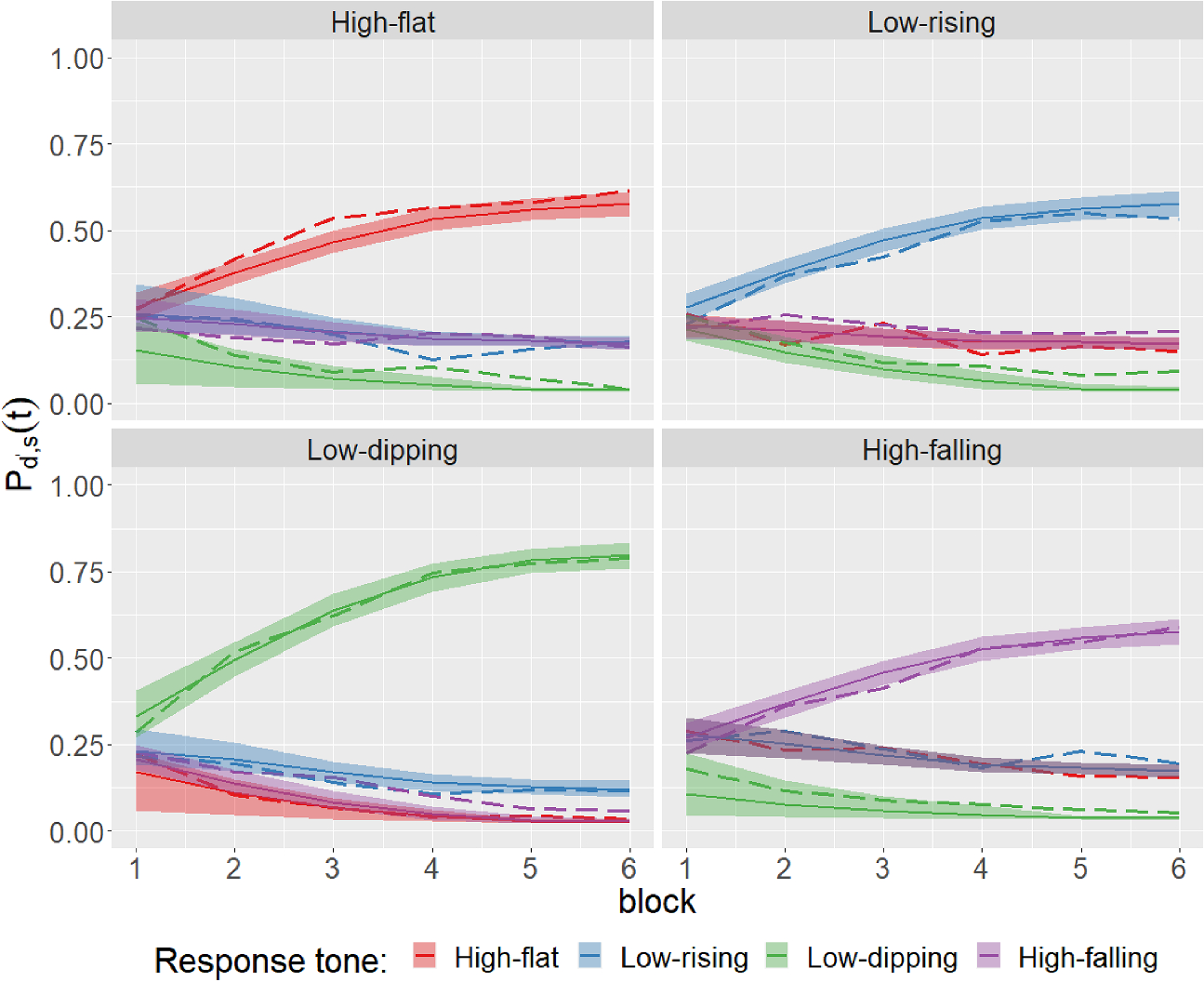
Figure 6 Results for PTC1 data: Estimated probability trajectories compared with average proportions of times an input tone was classified into different tone categories across subjects (in dashed line). The means across subjects are indicated by thick lines and the shaded regions indicate corresponding 95% coverage regions.
We observe that except for the input-response combination (1, 1) in block 3 and some cases with a low number of data points, the 95% credible intervals include the corresponding empirical probabilities. An explanation of the occasional under-performance is given later in this section.
Next, we examine the clusters identified by the proposed model. Apart from the two clusters obtained for the success combinations
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(d=s)$$\end{document}
![]() , three clusters are additionally identified in the incorrect input-response combinations
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(d\ne s)$$\end{document}
, three clusters are additionally identified in the incorrect input-response combinations
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(d\ne s)$$\end{document}
![]() . The clusters of success combinations are
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{1}=\{(1,1),(2,2),(4,4)\}$$\end{document}
. The clusters of success combinations are
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{1}=\{(1,1),(2,2),(4,4)\}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{2}=\{(3,3)\}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{2}=\{(3,3)\}$$\end{document}
![]() , and of wrong allocations are
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{1}=\{(1,2),(1,4),(2,1),(2,4),(3,2),(4,1),(4,2)\}$$\end{document}
, and of wrong allocations are
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{1}=\{(1,2),(1,4),(2,1),(2,4),(3,2),(4,1),(4,2)\}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{2}=\{(1,3),(2,3),(3,4),(4,3) \}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{2}=\{(1,3),(2,3),(3,4),(4,3) \}$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{3}=\{(3,1)\}$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{3}=\{(3,1)\}$$\end{document}
![]() . Figure 7 shows the input-response tone combinations color-coded as per cluster identity, and the proportion of times each pair of input-response tone combinations appeared in the same cluster after burnin. Figure 7 indicates that, while the clusters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{1}, S_{2}, M_{1}$$\end{document}
. Figure 7 shows the input-response tone combinations color-coded as per cluster identity, and the proportion of times each pair of input-response tone combinations appeared in the same cluster after burnin. Figure 7 indicates that, while the clusters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{1}, S_{2}, M_{1}$$\end{document}
![]() are stable, there is some instability among the other two clusters, namely
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{2}$$\end{document}
are stable, there is some instability among the other two clusters, namely
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{2}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{3}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{3}$$\end{document}
![]() .
.
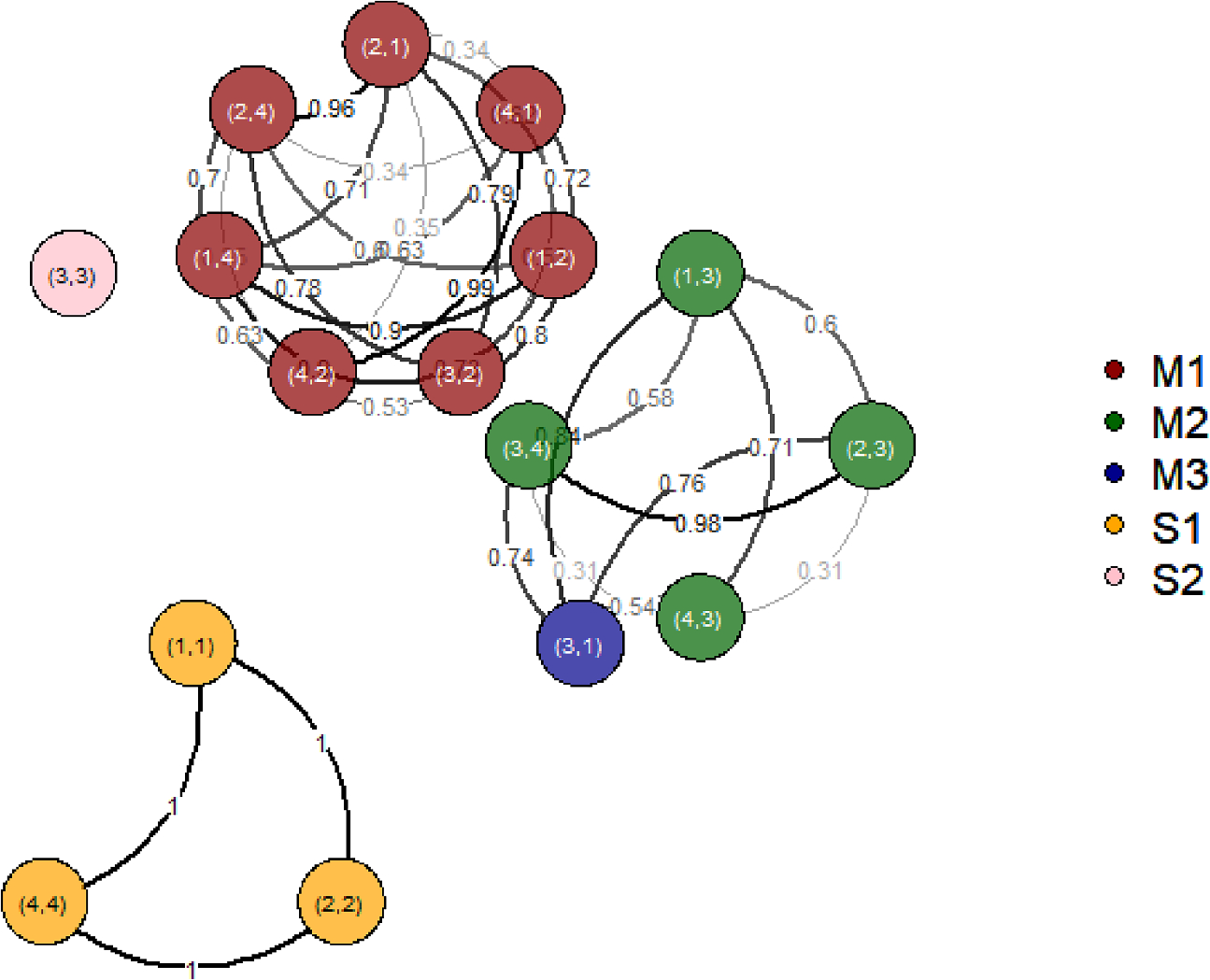
Figure 7 Results for PTC1 data: Network plot of similarity groups showing the intra- and inter-cluster similarities of tone recognition problems. Each node is associated with a pair indicating the input-response tone category, (s, d). The number associated with each edge indicates the proportion of times the pair in the two connecting nodes appeared in the same cluster after burnin.
Key Findings The clustering structure reveals that the low-dipping (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{3}$$\end{document}
![]() ) response trajectories are different from the other three response categories. While for correct input–output tone combinations,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{2}$$\end{document}
) response trajectories are different from the other three response categories. While for correct input–output tone combinations,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{2}$$\end{document}
![]() forms a separate singleton cluster, for incorrect combinations,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{2}$$\end{document}
forms a separate singleton cluster, for incorrect combinations,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{2}$$\end{document}
![]() contains all the low-dipping trajectories, indicating their similarities across the panels. Also for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{3}$$\end{document}
contains all the low-dipping trajectories, indicating their similarities across the panels. Also for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{3}$$\end{document}
![]() , faster increase of the probabilities of correct identification, as well as faster decay of probabilities of incorrect identification indicate that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{3}$$\end{document}
, faster increase of the probabilities of correct identification, as well as faster decay of probabilities of incorrect identification indicate that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{3}$$\end{document}
![]() is easily distinguishable from other alternatives.
is easily distinguishable from other alternatives.
On the other hand, the trajectories of high-flat (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{1}$$\end{document}
![]() ), low-rising (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{2}$$\end{document}
), low-rising (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{2}$$\end{document}
![]() ) and high-falling (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{4}$$\end{document}
) and high-falling (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{4}$$\end{document}
![]() ) response categories are quite similar across panels. While for correct input-response combinations, these three form the cluster
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{1}$$\end{document}
) response categories are quite similar across panels. While for correct input-response combinations, these three form the cluster
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{1}$$\end{document}
![]() , the corresponding incorrect tone combinations are clustered in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{1}$$\end{document}
, the corresponding incorrect tone combinations are clustered in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{1}$$\end{document}
![]() . The slower rise of the observed empirical probabilities for the elements in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{1}$$\end{document}
. The slower rise of the observed empirical probabilities for the elements in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{1}$$\end{document}
![]() and the slower decay of the same for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{1}$$\end{document}
and the slower decay of the same for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M_{1}$$\end{document}
![]() indicate that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{1}$$\end{document}
indicate that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{1}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{2}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{2}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{4}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{4}$$\end{document}
![]() are difficult to distinguish. However, in block 3 the empirical probabilities of correct input-response combinations differ moderately. While
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{2}$$\end{document}
are difficult to distinguish. However, in block 3 the empirical probabilities of correct input-response combinations differ moderately. While
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{2}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{4}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{4}$$\end{document}
![]() show a relative drop in the empirical probabilities at block 3,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{1}$$\end{document}
show a relative drop in the empirical probabilities at block 3,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{1}$$\end{document}
![]() shows a sudden pick in the same. This local dissimilarity of the trajectories at block 3, leads to a departure of the empirical probability of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{1}$$\end{document}
shows a sudden pick in the same. This local dissimilarity of the trajectories at block 3, leads to a departure of the empirical probability of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T_{1}$$\end{document}
![]() from the estimated credible band.
from the estimated credible band.
Next, we consider the results concerning the estimation of the drift parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}^{(i)}(t)$$\end{document}
![]() . As discussed in Sect. 2.2, given the identifiability constraints, the estimates of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}^{(i)}(t)$$\end{document}
. As discussed in Sect. 2.2, given the identifiability constraints, the estimates of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}^{(i)}(t)$$\end{document}
![]() can only be interpreted on a relative scale. Figure 8 shows the posterior mean trajectories and associated 95% credible intervals for the projected drift rates.
can only be interpreted on a relative scale. Figure 8 shows the posterior mean trajectories and associated 95% credible intervals for the projected drift rates.
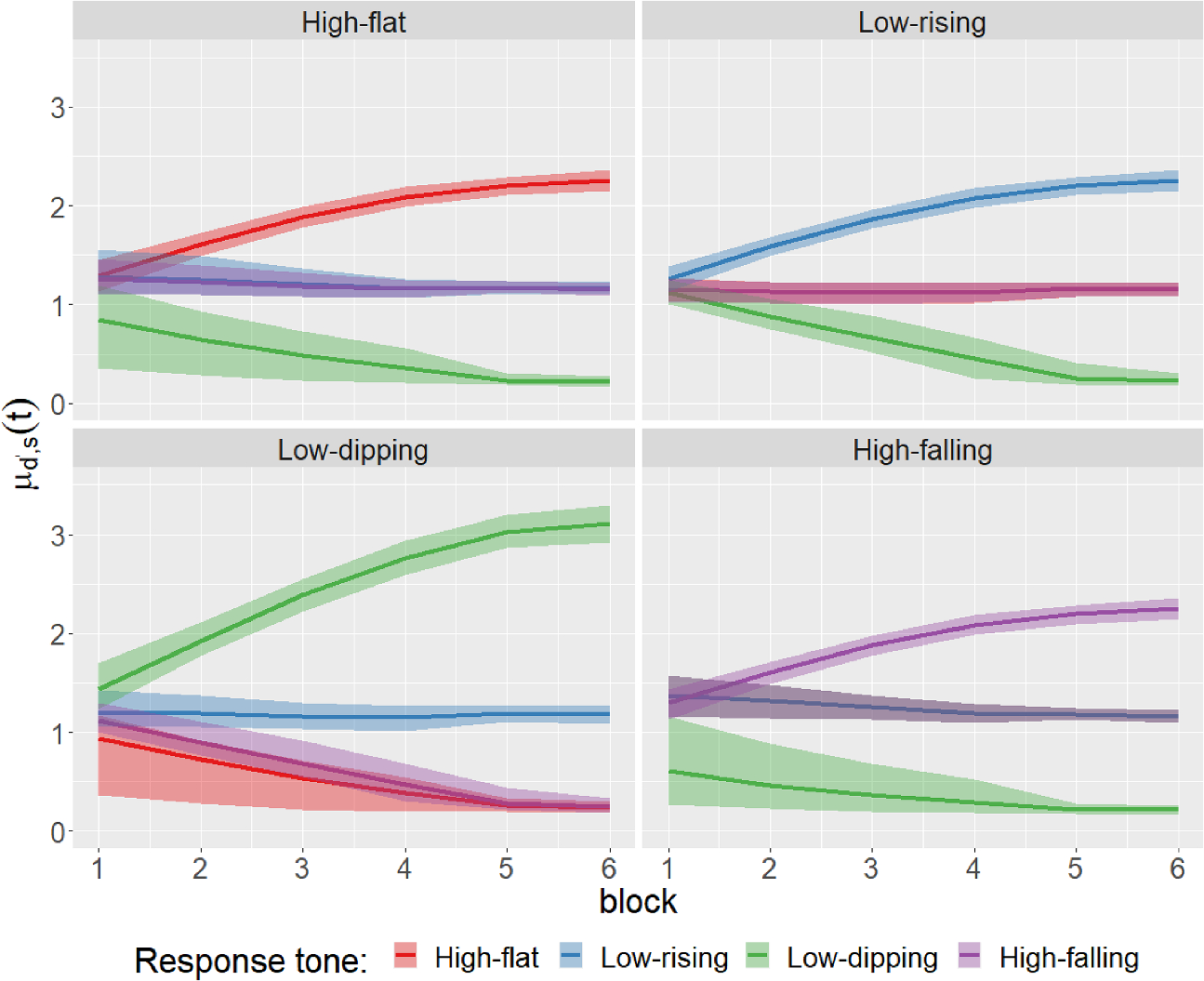
Figure 8 Results for PTC1 data: Estimated posterior mean trajectories of the population level drifts
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}(t)$$\end{document}
![]() for the proposed model. The shaded areas represent the corresponding 95% point-wise credible intervals.
for the proposed model. The shaded areas represent the corresponding 95% point-wise credible intervals.
Importantly, our proposed mixed model also allows us to assess individual-specific parameter trajectories. Figure 9 shows the posterior mean trajectories and the associated 95% credible intervals for the drift rates
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}^{(i)}$$\end{document}
![]() estimated by our method for the different success combinations
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(d^{\prime },s)$$\end{document}
estimated by our method for the different success combinations
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(d^{\prime },s)$$\end{document}
![]() for two participants—one with the best accuracy averaged across all blocks, and the other with the worst accuracy averaged across all blocks. These results suggest significant individual-specific heterogeneity. For the well-performing participant, the drift parameters are much higher than those for the poorly performing individual, indicating their ability to more quickly accumulate evidence compared to the poorly performing adult. These differences persisted over all blocks with a small gradual increase over time.
for two participants—one with the best accuracy averaged across all blocks, and the other with the worst accuracy averaged across all blocks. These results suggest significant individual-specific heterogeneity. For the well-performing participant, the drift parameters are much higher than those for the poorly performing individual, indicating their ability to more quickly accumulate evidence compared to the poorly performing adult. These differences persisted over all blocks with a small gradual increase over time.
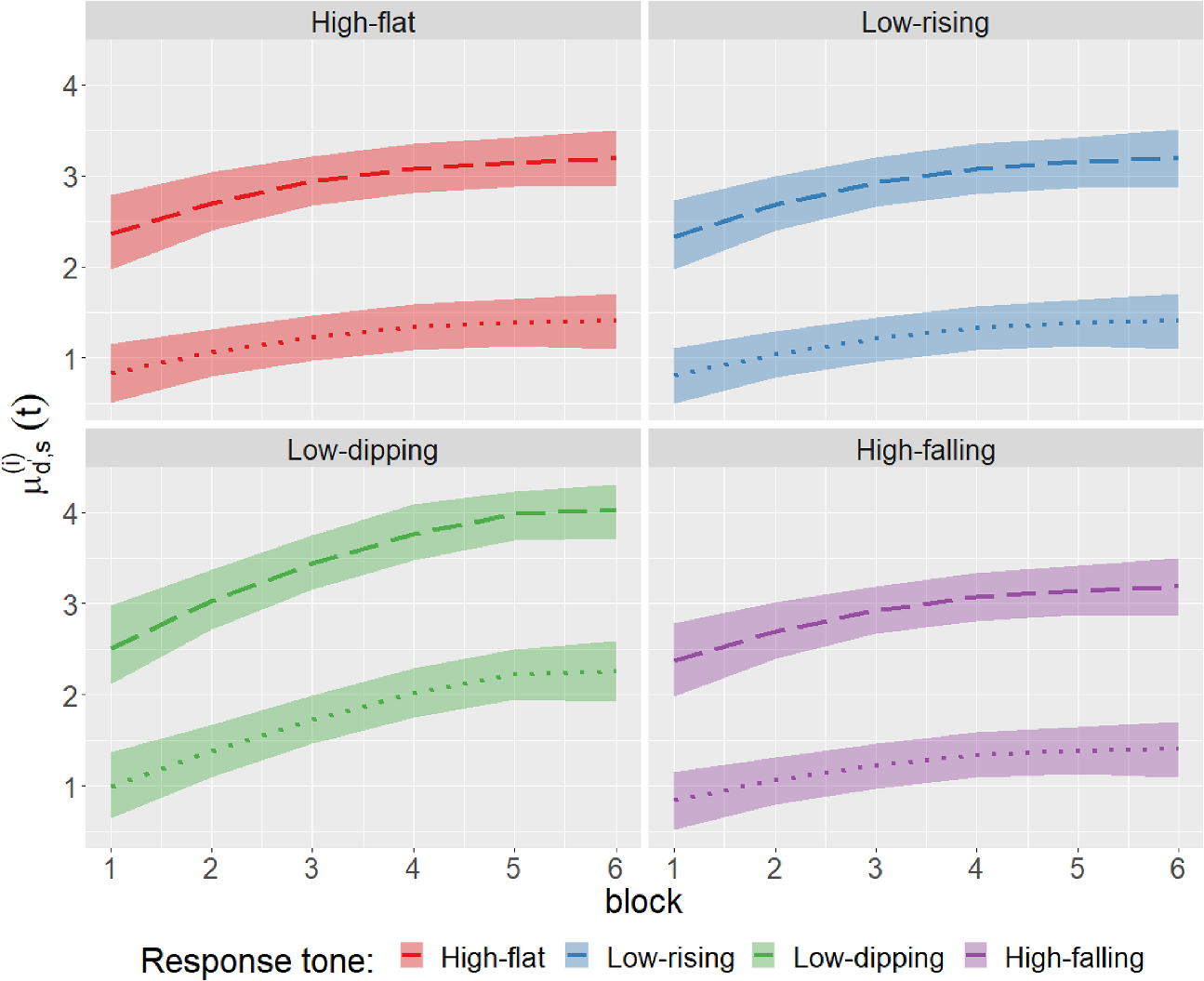
Figure 9 Results for PTC1 data: Estimated posterior mean trajectories for individual specific drifts
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}^{(i)}(t) = \exp \{ f_{d^{\prime },s}(t) + u_{C}^{(i)}(t) \}$$\end{document}
![]() for successful identification
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(d^{\prime }=s)$$\end{document}
for successful identification
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(d^{\prime }=s)$$\end{document}
![]() for two different participants—one performing well (dashed line) and one performing poorly (dotted line). The shaded areas represent the corresponding 95% point-wise credible intervals.
for two different participants—one performing well (dashed line) and one performing poorly (dotted line). The shaded areas represent the corresponding 95% point-wise credible intervals.
Analysis of Benchmark Data To validate the proposed method, we also analyzed tone learning data which, in addition to response accuracies, included accurate measurements of the response times. It was previously analyzed in Paulon et al. (Reference Paulon, Llanos, Chandrasekaran and Sarkar2021) using the drift-diffusion model (2) which allowed inference on both the drift and the boundary parameters. For our analysis with the method proposed here, however, we ignored the response times. We observed that the estimates of the drifts produced by our proposed methodology match well with the estimates obtained by Paulon et al. (Reference Paulon, Llanos, Chandrasekaran and Sarkar2021). A description of this ‘benchmark’ data set and other details of our analyses are provided in Section S.5 of the supplementary material.
7. Discussion, Conclusion, Broader Utility, and Future Work
Summary In this article, we developed a novel longitudinal inverse-probit mixed categorical probability model. Our research was motivated by category learning experiments where scientists are interested in using drift-diffusion models to understand how the decision-making mechanisms evolve as the participants get more training and experience. However, unlike traditional drift-diffusion analyses which require data on both response categories and response times, we only had usable records of response categories but no response times. To our knowledge, biologically interpretable latent drift-diffusion process-based categorical probability models had never been considered for such scenarios in the literature before. We addressed this need. Building on a previous work on longitudinal drift-diffusion mixed joint models for response categories and response times but now integrating out the response times, we obtained a new class of category probability models which we referred to here as the inverse-probit model. We explored parameter recoverability in such models, showing, in particular, that the offset parameters can not be recovered and drifts and boundaries both can not be recovered from data only on response categories. In our analyses, we thus focused on estimating the biologically more important drift parameters but kept the offsets and the boundaries fixed. We showed that with careful domain knowledge informed choices for the boundaries, the general trajectories of the drift parameters can be recovered by our proposed approach even in the complete absence of response times.
Conclusion Overall, when it comes to making scientific inferences about drift-diffusion model parameters in the absence of data on response times, our work implies a mixed promise. On the downside, our work shows that the detailed interplay between drifts and boundaries cannot be captured. On the positive side, our results also suggest that, with our carefully designed model, and the fixed value of the boundary parameters appropriately chosen by experts, the general longitudinal trends in the drifts can still be estimated well from data only on response categories. Caution should still be exercised not to over-interpret the results.
Broader Utility in Auditory Neuroscience The proposed model, we believe, has significant implications for auditory neuroscience. We focused here specifically on a pupillometry study for which the experimental paradigms need to be adapted to prioritize slow pupillary response, rendering the behavioral response times useless. However, as discussed in the Introduction, there could be many other situations where usable data on response times may not be available. The proposed model can be useful in such scenarios to understand the perceptual mechanisms underlying auditory decision-making.
Broader Utility Beyond Auditory Neuroscience While we focused here on studying auditory category learning, the method proposed is applicable to other domains of behavioral neuroscience research studying categorical decision-making when the response times measurements are either not available or not reliable.
Broader Utility in Statistics On the statistical side, the projection-based approach proposed here to impose non-standard identifiability conditions and address clustering problems within and between different panels is not restricted to inverse-probit models introduced here. They can be easily adapted to other classes of generalized linear models such as the widely popular logit and probit models and hence may also be of interest to a much broader statistical audience.
Future Directions The models and the analyses of the PTC1 data set presented here excluded the pupillometry measurements themselves. An important and challenging problem being pursued separately elsewhere is to see how those measurements relate to drift-diffusion model parameters.
Funding
This research was funded by the National Science Foundation grant DMS 1953712 and National Institute on Deafness and Other Communication Disorders Grants R01DC013315 and R01DC015504 awarded to Sarkar and Chandrasekaran.
Appendix
Appendix A: Proof of Lemma 1
Proof. It is easy to check that the offset parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\delta _{s}$$\end{document}
![]() are not identifiable since
are not identifiable since
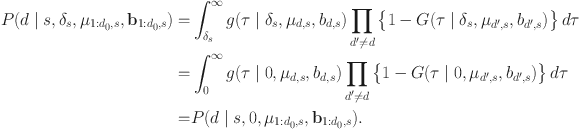
Next we will show that the drift parameters and decision boundaries are not separately identifiable, even if we fix offset parameters to a constant.
First note that Eq. (3) can also be represented as
First observe that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau ^{\star }=\wedge _{d^{\prime }\ne d}\tau _{d^{\prime }} =\tau _{-1}^{\star }\wedge \tau _{1}$$\end{document}
![]() , where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{-1}^{\star }=\wedge _{d^{\prime }\ne \{1,d\}}\tau _{d^{\prime }}$$\end{document}
, where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{-1}^{\star }=\wedge _{d^{\prime }\ne \{1,d\}}\tau _{d^{\prime }}$$\end{document}
![]() . Thus the integral above can be written as
. Thus the integral above can be written as
Proceeding sequentially one can show that the integral above is the same as in (3).
Using the above we express the probability in (3) as in (A.1). As the offset parameter
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\delta _{s}$$\end{document}
![]() is already shown to be not identifiable, we need to fix the same. Without loss of generality, we fix the offset parameter at 0. The probability density function of inverse Gaussian distribution, with parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\theta }_{d^{\prime },s}=(\mu _{d^{\prime },s},b_{d^{\prime },s})$$\end{document}
is already shown to be not identifiable, we need to fix the same. Without loss of generality, we fix the offset parameter at 0. The probability density function of inverse Gaussian distribution, with parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\theta }_{d^{\prime },s}=(\mu _{d^{\prime },s},b_{d^{\prime },s})$$\end{document}
![]() evaluated at
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d^{\prime }}$$\end{document}
evaluated at
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d^{\prime }}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g(\tau _{d^{\prime }}\mid {\theta }_{d^{\prime },s})$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g(\tau _{d^{\prime }}\mid {\theta }_{d^{\prime },s})$$\end{document}
![]() can be obtained from (1) by replacing
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\delta _{s}=0$$\end{document}
can be obtained from (1) by replacing
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\delta _{s}=0$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=d^{\prime }$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=d^{\prime }$$\end{document}
![]() .
.
Consider the transformation of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d^{\prime }}$$\end{document}
![]() to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d^{\prime }}^{\star }$$\end{document}
to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d^{\prime }}^{\star }$$\end{document}
![]() as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d^{\prime }}=c^2\tau _{d^{\prime }}^{\star }$$\end{document}
as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d^{\prime }}=c^2\tau _{d^{\prime }}^{\star }$$\end{document}
![]() , for some constant
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$c>0$$\end{document}
, for some constant
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$c>0$$\end{document}
![]() , and for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d^{\prime }$$\end{document}
, and for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d^{\prime }$$\end{document}
![]() . Further, define
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d^{\prime },s}^{\star }=b_{d^{\prime },s}/c$$\end{document}
. Further, define
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d^{\prime },s}^{\star }=b_{d^{\prime },s}/c$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}^{\star }=c\mu _{d^{\prime },s}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}^{\star }=c\mu _{d^{\prime },s}$$\end{document}
![]() , for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d^{\prime }$$\end{document}
, for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d^{\prime }$$\end{document}
![]() . Then observe that
. Then observe that
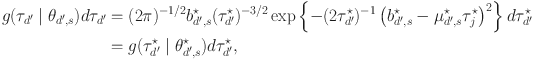
where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g(\tau _{d^{\prime }}^{\star }\mid {\theta }_{d^{\prime },s}^{\star } )$$\end{document}
![]() is the pdf of inverse Gaussian distribution with parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}^{\star }$$\end{document}
is the pdf of inverse Gaussian distribution with parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{d^{\prime },s}^{\star }$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d^{\prime },s}^{\star }$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$b_{d^{\prime },s}^{\star }$$\end{document}
![]() , evaluated at the point
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d^{\prime }}^{\star }$$\end{document}
, evaluated at the point
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d^{\prime }}^{\star }$$\end{document}
![]() .
.
Applying the transformation on
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d^{\prime }}$$\end{document}
![]() for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d^{\prime }$$\end{document}
for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d^{\prime }$$\end{document}
![]() we get that the integral in (A.1) with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\delta _{s}=0$$\end{document}
we get that the integral in (A.1) with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\delta _{s}=0$$\end{document}
![]() is same as
is same as
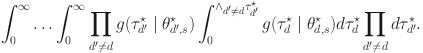
As c is arbitrary, this shows that the drifts and boundaries are not separately estimable.
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\square $$\end{document}
![]()
Appendix B: Proof of Theorem 1
Proof. Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\textbf{P}}}({\mu }_{1:d_{0},s})=\{p_{1}({\mu }_{1:d_{0},s}), \dots , p_{d_{0}}({\mu }_{1:d_{0},s}) \}^\textrm{T}$$\end{document}
![]() be the function, given by (4), from
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{0,k}$$\end{document}
be the function, given by (4), from
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{0,k}$$\end{document}
![]() to unit probability simplex
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Delta ^{d_{0}-1}$$\end{document}
to unit probability simplex
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Delta ^{d_{0}-1}$$\end{document}
![]() . For notational simplicity, we write
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s} = {\mu }= (\mu _{1}, \dots , \mu _{d_{0}})^\textrm{T}$$\end{document}
. For notational simplicity, we write
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }_{1:d_{0},s} = {\mu }= (\mu _{1}, \dots , \mu _{d_{0}})^\textrm{T}$$\end{document}
![]() . We first find the matrix of partial derivative
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\nabla {{\textbf{P}}}$$\end{document}
. We first find the matrix of partial derivative
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\nabla {{\textbf{P}}}$$\end{document}
![]() with respect to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }$$\end{document}
with respect to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }$$\end{document}
![]() .
.
For
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }\in \mathcal{S}_{0,k}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$ \textbf{1}^{T} {\mu }=k$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$ \textbf{1}^{T} {\mu }=k$$\end{document}
![]() , and hence the probability reduces to
, and hence the probability reduces to
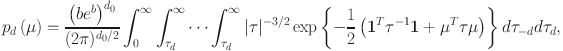
for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1,\ldots , d_{0}$$\end{document}
![]() , where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\tau }=\textrm{diag}(\tau _{1}, \ldots , \tau _{d_{0}})$$\end{document}
, where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\tau }=\textrm{diag}(\tau _{1}, \ldots , \tau _{d_{0}})$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\tau }_{-d}$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\tau }_{-d}$$\end{document}
![]() is the sub-vector of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\tau }$$\end{document}
is the sub-vector of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\tau }$$\end{document}
![]() excluding the d-th element. Next, differentiating
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$p_{d}\left( {\mu }\right) $$\end{document}
excluding the d-th element. Next, differentiating
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$p_{d}\left( {\mu }\right) $$\end{document}
![]() with respect to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }$$\end{document}
with respect to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }$$\end{document}
![]() , we get
, we get
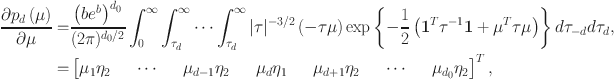
where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$ \eta _{1} = - E\left\{ \tau _{1} {\mathbb {I}}\left( \tau _{2}> \tau _{1}, \ldots , \tau _{d_{0}}>\tau _{1}\right) \left| {\mu }\right. \right\} $$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$ \eta _{2} = -E\left\{ \tau _{2} {\mathbb {I}}\left( \tau _{2}> \tau _{1}, \ldots , \tau _{d_{0}}>\tau _{1}\right) \left| {\mu }\right. \right\} $$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$ \eta _{2} = -E\left\{ \tau _{2} {\mathbb {I}}\left( \tau _{2}> \tau _{1}, \ldots , \tau _{d_{0}}>\tau _{1}\right) \left| {\mu }\right. \right\} $$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mathbb {I}}(A)$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mathbb {I}}(A)$$\end{document}
![]() is the indicator function of the event A. Here the expectation is considered under the joint distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left( \tau _{1}, \ldots , \tau _{d}\right) $$\end{document}
is the indicator function of the event A. Here the expectation is considered under the joint distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left( \tau _{1}, \ldots , \tau _{d}\right) $$\end{document}
![]() , which is independent inverse Gaussian. Clearly
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\eta _{1}>\eta _{2}>0$$\end{document}
, which is independent inverse Gaussian. Clearly
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\eta _{1}>\eta _{2}>0$$\end{document}
![]() .
.
From the above derivation, it is easy to obtain that

where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\textbf{M}}}=\textrm{diag}\left( \mu _{1}, \ldots , \mu _{d_{0}}\right) $$\end{document}
![]() .
.
Now, suppose there exists
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\nu }$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\nu }$$\end{document}
![]() in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{k}$$\end{document}
in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{k}$$\end{document}
![]() such that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }\ne {\nu }$$\end{document}
such that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }\ne {\nu }$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\textbf{P}}}\left( {\mu }\right) = {{\textbf{P}}}\left( {\nu }\right) $$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\textbf{P}}}\left( {\mu }\right) = {{\textbf{P}}}\left( {\nu }\right) $$\end{document}
![]() . Define
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\gamma }: [0,1] \rightarrow {\mathbb {R}}^{d_{0}}$$\end{document}
. Define
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\gamma }: [0,1] \rightarrow {\mathbb {R}}^{d_{0}}$$\end{document}
![]() such that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\gamma }(t)= {\mu }+ t \left( {\nu }- {\mu }\right) $$\end{document}
such that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\gamma }(t)= {\mu }+ t \left( {\nu }- {\mu }\right) $$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$t\in [0,1]$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$t\in [0,1]$$\end{document}
![]() . Further, define
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$h(t)= \langle {{\textbf{P}}}\left( {\gamma }(t) \right) - {{\textbf{P}}}\left( {\mu }\right) , {\nu }- {\mu }\rangle $$\end{document}
. Further, define
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$h(t)= \langle {{\textbf{P}}}\left( {\gamma }(t) \right) - {{\textbf{P}}}\left( {\mu }\right) , {\nu }- {\mu }\rangle $$\end{document}
![]() , as the cross-product of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\textbf{P}}}\left( {\gamma }(t) \right) - {{\textbf{P}}}\left( {\mu }\right) $$\end{document}
, as the cross-product of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\textbf{P}}}\left( {\gamma }(t) \right) - {{\textbf{P}}}\left( {\mu }\right) $$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\nu }-{\mu }$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\nu }-{\mu }$$\end{document}
![]() . Then
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$h(1)=h(0)=0$$\end{document}
. Then
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$h(1)=h(0)=0$$\end{document}
![]() under the proposition that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\textbf{P}}}\left( {\mu }\right) = {{\textbf{P}}}\left( {\nu }\right) $$\end{document}
under the proposition that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\textbf{P}}}\left( {\mu }\right) = {{\textbf{P}}}\left( {\nu }\right) $$\end{document}
![]() . Therefore, by the Mean Value Theorem, as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }\ne {\nu }$$\end{document}
. Therefore, by the Mean Value Theorem, as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }\ne {\nu }$$\end{document}
![]() , there exists some point
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$c\in (0,1)$$\end{document}
, there exists some point
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$c\in (0,1)$$\end{document}
![]() such that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left. \partial h(t) / \partial t \right| _{t=c} =0$$\end{document}
such that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left. \partial h(t) / \partial t \right| _{t=c} =0$$\end{document}
![]() . Now,
. Now,
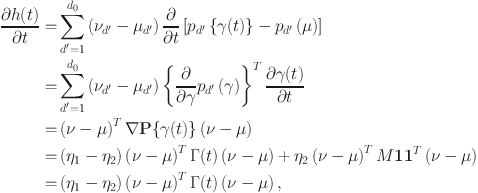
as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{1}^{T} \left( {\nu }-{\mu }\right) =0$$\end{document}
![]() , where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\Gamma }(t)=\textrm{diag}\{ {\gamma }(t) \}$$\end{document}
, where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\Gamma }(t)=\textrm{diag}\{ {\gamma }(t) \}$$\end{document}
![]() .
.
As every component of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\nu }$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\nu }$$\end{document}
![]() is positive, for any
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$c\in (0,1)$$\end{document}
is positive, for any
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$c\in (0,1)$$\end{document}
![]() , the matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\Gamma }(c)$$\end{document}
, the matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\Gamma }(c)$$\end{document}
![]() is positive definite. Further, as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\eta _{1}>\eta _{2}$$\end{document}
is positive definite. Further, as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\eta _{1}>\eta _{2}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left. \partial h(t) / \partial t \right| _{t=c} =0$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left. \partial h(t) / \partial t \right| _{t=c} =0$$\end{document}
![]() only if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$ {\mu }={\nu }$$\end{document}
only if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$ {\mu }={\nu }$$\end{document}
![]() , which contradicts the proposition.
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\square $$\end{document}
, which contradicts the proposition.
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\square $$\end{document}
![]()
Appendix C: Algorithm for Minimal Distance Mapping
The problem of finding projection of a point
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }$$\end{document}
![]() onto the space
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{k,\varepsilon }$$\end{document}
onto the space
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{k,\varepsilon }$$\end{document}
![]() is equivalent to the following nonlinear optimization problem:
is equivalent to the following nonlinear optimization problem:
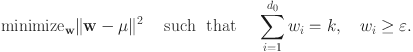
Duchi et al. (Reference Duchi, Shalev-Shwartz, Singer and Chandra2008, Algorithm 1) provides a solution to the problem of projection of a given point
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mu }$$\end{document}
![]() onto the space
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{k,\varepsilon }$$\end{document}
onto the space
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{S}_{k,\varepsilon }$$\end{document}
![]() for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varepsilon =0$$\end{document}
for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varepsilon =0$$\end{document}
![]() , which is modified for any given
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varepsilon $$\end{document}
, which is modified for any given
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varepsilon $$\end{document}
![]() below.
below.
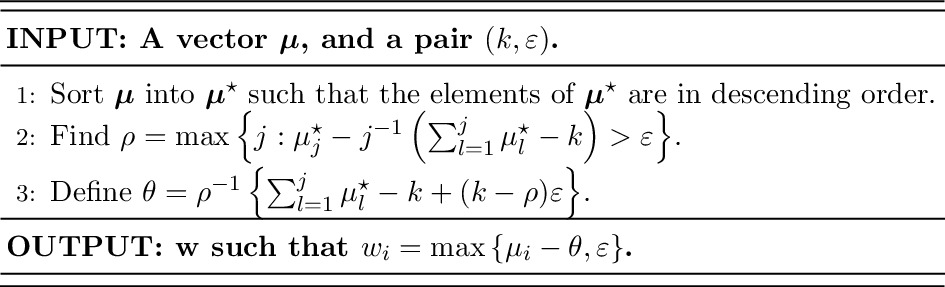
Appendix D: Proof of Lemma 3
Proof. We consider the unconditional distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{1:d_{0}}$$\end{document}
![]() , given the parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{1:d_{0}}$$\end{document}
, given the parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{1:d_{0}}$$\end{document}
![]() as the proposal distribution, g. Clearly, the proposal distribution g and the target conditional joint distribution f satisfies
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$f(\tau _{1:d_{0}}|\mu _{1:d_{0}})/g(\tau _{1:d_{0}}|\mu _{1:d_{0}})\le M$$\end{document}
as the proposal distribution, g. Clearly, the proposal distribution g and the target conditional joint distribution f satisfies
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$f(\tau _{1:d_{0}}|\mu _{1:d_{0}})/g(\tau _{1:d_{0}}|\mu _{1:d_{0}})\le M$$\end{document}
![]() , where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M^{-1}=P\left( \tau _{d} \le \tau _{1:d_{0}}\right) $$\end{document}
, where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$M^{-1}=P\left( \tau _{d} \le \tau _{1:d_{0}}\right) $$\end{document}
![]() . Therefore, for any random sample
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$U\sim U(0,1)$$\end{document}
. Therefore, for any random sample
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$U\sim U(0,1)$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$f(\tau _{1:d_{0}}|\mu _{1:d_{0}})\ge M U g(\tau _{1:d_{0}}|\mu _{1:d_{0}})$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$f(\tau _{1:d_{0}}|\mu _{1:d_{0}})\ge M U g(\tau _{1:d_{0}}|\mu _{1:d_{0}})$$\end{document}
![]() if the sample satisfies the condition
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d} \le \tau _{1:d_{0}}$$\end{document}
if the sample satisfies the condition
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{d} \le \tau _{1:d_{0}}$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$f(\tau _{1:d_{0}}|\mu _{1:d_{0}})< M U g(\tau _{1:d_{0}}|\mu _{1:d_{0}})$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$f(\tau _{1:d_{0}}|\mu _{1:d_{0}})< M U g(\tau _{1:d_{0}}|\mu _{1:d_{0}})$$\end{document}
![]() otherwise. Hence, by Lemma 2.3.1 of Robert and Casella (Reference Robert and Casella2004), algorithm above produces samples from the target distribution.
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\square $$\end{document}
otherwise. Hence, by Lemma 2.3.1 of Robert and Casella (Reference Robert and Casella2004), algorithm above produces samples from the target distribution.
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\square $$\end{document}
![]()



































