Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2025-01-04T03:59:34.208Z Has data issue: false hasContentIssue false
  • English
  • Français

An Extended GFfit Statistic Defined on Orthogonal Components of Pearson’s Chi-Square

Published online by Cambridge University Press:  01 January 2025

Mark Reiser Open the ORCID record for Mark Reiser [Opens in a new window] ,
Silvia Cagnone  and
Junfei Zhu
Mark Reiser*
Affiliation:
Arizona State University
Silvia Cagnone
Affiliation:
University of Bologna
Junfei Zhu
Affiliation:
Arizona State University
*
Correspondence should be made to Mark Reiser, School of Mathematical and Statistical Sciences, Arizona State University, Tempe, AZ85287, USA. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The Pearson and likelihood ratio statistics are commonly used to test goodness of fit for models applied to data from a multinomial distribution. The goodness-of-fit test based on Pearson’s Chi-squared statistic is sometimes considered to be a global test that gives little guidance to the source of poor fit when the null hypothesis is rejected, and it has also been recognized that the global test can often be outperformed in terms of power by focused or directional tests. For the cross-classification of a large number of manifest variables, the GFfit statistic focused on second-order marginals for variable pairs i, j has been proposed as a diagnostic to aid in finding the source of lack of fit after the model has been rejected based on a more global test. When data are from a table formed by the cross-classification of a large number of variables, the common global statistics may also have low power and inaccurate Type I error level due to sparseness in the cells of the table. The sparseness problem is rarely encountered with the GFfit statistic because it is focused on the lower-order marginals. In this paper, a new and extended version of the GFfit statistic is proposed by decomposing the Pearson statistic from the full table into orthogonal components defined on marginal distributions and then defining the new version, GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document}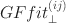, as a partial sum of these orthogonal components. While the emphasis is on lower-order marginals, the new version of GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document} 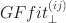is also extended to higher-order tables so that the GFfit⊥\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }$$\end{document} 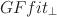statistics sum to the Pearson statistic. As orthogonal components of the Pearson X2\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$X^2$$\end{document} 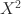statistic, GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document} 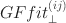statistics have advantages over other lack-of-fit diagnostics that are currently available for cross-classified tables: the GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document} 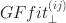generally have higher power to detect lack of fit while maintaining good Type I error control even if the joint frequencies are very sparse, as will be shown in simulation results; theoretical results will establish that GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document} 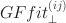statistics have known degrees of freedom and are asymptotically independent with known joint distribution, a property which facilitates less conservative control of false discovery rate (FDR) or familywise error rate (FWER) in a high-dimensional table which would produce a large number of bivariate lack-of-fit diagnostics. Computation of GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document} 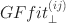statistics is also computationally stable. The extended GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document} 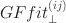statistic can be applied to a variety of models for cross-classified tables. An application of the new GFfit statistic as a diagnostic for a latent variable model is presented.

Keywords

multivariate discrete distributionoverlapping cellsorthogonal componentscomposite null hypothesis
Type
Theory and Methods
Information
Psychometrika , Volume 88 , Issue 1 , March 2023 , pp. 208 - 240
Copyright
Copyright © 2022 The Author(s) under exclusive licence to The Psychometric Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Supplementary Information The online version contains supplementary material available at https://doi.org/10.1007/s11336-022-09866-6.

References

Afifi, A. A., & Clark, V. (1984). Computer-aided multivariate analysis. Lifetime Learning Publications.Google Scholar
Agresti, A., Yang, M. C., (1987). An empirical investigation of some effects of sparseness in contingency tables Computational Statistics & Data Analysis 5 9–21 10.1016/0167-9473(87)90003-XCrossRefGoogle Scholar
Asparouhov, T., & Muthén, B. (2010). Simple second order chi-square correction. Mplus technical report. https://www.statmodel.com/download/WLSMV_new_chi21.pdf. Accessed 18 Feb 2018Google Scholar
Bartholomew, D. J. (1987). Latent variable models and factor analysis. Oxford University Press.Google Scholar
Bartholomew, D. J., Leung, S. O., (2002). A goodness-of-fit test for sparse 2 p \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$2^p$$\end{document} contingency tables British Journal of Mathematical and Statistical Psychology 55 1–15 10.1348/000711002159617 12034008CrossRefGoogle Scholar
Benjamini, Y., Hochberg, Y., (1995). Controlling the false discovery rate: A practical and powerful approach to multiple testing Journal of the Royal Statistical Society: Series B (Methodological) 57(1) 289–300CrossRefGoogle Scholar
Benjamini, Y., Yekutieli, D., (2001). The control of the false discovery rate in multiple testing under dependency Annals of Statistics 29(4) 1165–1188 10.1214/aos/1013699998CrossRefGoogle Scholar
Birch, M. W. (1964). A new proof of the Pearson-Fisher theorem. Annals of Mathematical Statistics, 35, 818–824.CrossRefGoogle Scholar
Bock, R. D., (1972). Estimating item parameters and latent ability when responses are scored in two or more nominal categories Psychometrika 37 29–51 10.1007/BF02291411CrossRefGoogle Scholar
Breinegaard, N., Rabe-Hesketh, S. & Skrondal, A. (2018). Pairwise residuals and diagnostic tests for misspecified dependence structures in models for binary longitudinal data. Statistics in Medicine, 37(3), 343–356.CrossRefGoogle Scholar
Cagnone, S., Mignani, S., (2007). Assessing the goodness of fit for a latent variable model for ordinal data Metron LXV 337–361Google Scholar
Cai, L., & Hansen, M. (2013). Limited-information goodness-of-fit testing of hierarchical item factor models. British Journal of Mathematical and Statistical Psychology, 66, 245–276.CrossRefGoogle Scholar
Cai, L., Maydeu-Olivares, A., Coffman, D., Thissen, D., (2006). Limited information goodness-of-fit testing of item response theory models for sparse 2 p \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$2^p$$\end{document} tables British Journal of Mathematical and Statistical Psychology 59 173–194 10.1348/000711005X66419 16709285CrossRefGoogle Scholar
Christoffersson, A., (1975). Factor analysis of dichotomized variables Psychometrika 40 5–32 10.1007/BF02291477CrossRefGoogle Scholar
Dassanayake, M., Reiser, M., & Zhu, J. (2016). Power calculations for statistics based on orthogonal components of Pearson’s chi-square. In Alexandria, V. A. (Ed.), JSM proceedings, biometrics section (pp. 1079–1093). American Statistical Association.Google Scholar
Eubank, R. L., (1997). Testing goodness of fit with multinomial data Journal of the American Statistical Association 92(439) 1084–1093 10.1080/01621459.1997.10474064CrossRefGoogle Scholar
Glas, C. A., (1988). The derivation of some tests for the Rasch model from the multinomial distribution Psychometrika 53 525–546 10.1007/BF02294405CrossRefGoogle Scholar
Glas, C. A., (1999). Modification indices for the 2-PL and the nominal response model Psychometrika 64(3) 273–294 10.1007/BF02294296CrossRefGoogle Scholar
Glas, C. A., Suárez Falcón, J. D., (2003). A comparison of item fit statistics for the three-parameter logistic model Applied Psychological Measurement 27 265–289 10.1177/0146621602250530CrossRefGoogle Scholar
Glas, C. A., & Verhelst, N. D. (1995). Testing the Rasch model. Rasch models (pp. 69–95). Springer. https://doi.org/10.1007/978-1-4612-4230-7-5.CrossRefGoogle Scholar
Haberman, S. J., (1973). The analysis of residuals in cross-classified tables Biometrics 29 205–220 10.2307/2529686CrossRefGoogle Scholar
Houseman, E. A., Ryan, L. M., Coull, B. A., (2004). Cholesky residuals for assessing normal errors in a linear model with correlated outcomes Journal of the American Statistical Association 99(486) 383–394 10.1198/016214504000000403CrossRefGoogle Scholar
Jacqmin-Gadda, H., Sibillot, S., Proust, C., Molina, J-M Thiebaut, R., (2007). Robustness of the linear mixed model to misspecified error distribution Computational Statistics & Data Analysis 51(10) 5142–5154 10.1016/j.csda.2006.05.021CrossRefGoogle Scholar
Jöreskog, K. G., & Moustaki, I. (2001). Factor analysis of ordinal variables: A comparison of three approaches. Multivariate Behavioral Research, 36, 347–387.CrossRefGoogle Scholar
Koehler, K. J., (1986). Goodness-of-fit tests for log-linear models in sparse contingency tables Journal of the American Statistical Association 81 336–344 10.1080/01621459.1986.10478294CrossRefGoogle Scholar
Koehler, K. J., Larntz, K., (1980). An empirical investigation of goodness-of-fit statistics for sparse multinomials Journal of the American Statistical Association 75 336–344 10.1080/01621459.1980.10477473CrossRefGoogle Scholar
Lancaster, H. O. (1969). The chi-squared distribution. Wiley.Google Scholar
Liu, Y., Maydeu-Olivares, A., (2012). Local dependence diagnostics in IRT modeling of binary data Educational and Psychological Measurement 73(2) 254–274 10.1177/0013164412453841CrossRefGoogle Scholar
Liu, Y., Maydeu-Olivares, A., (2014). Identifying the source of misfit in item response theory models Multivariate Behavioral Research 49 354–371 10.1080/00273171.2014.910744 26765803CrossRefGoogle ScholarPubMed
Magnus, J. R., & Neudecker, H. (1999). Matrix differential calculus with applications in statistics and econometrics. Wiley & Sons.Google Scholar
Mavridis, D., Moustaki, I., Knott, M., Lee, S-Y (2007). Goodness-of-fit measures for latent variable models for binary data Handbook of Latent Variable and Related Models Amsterdam, The Netherlands Elsevier 135–161Google Scholar
Maydeu-Olivares, A., Joe, H., (2005). Limited- and full-information estimation and goodness-of-fit testing in 2 n \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$2^{n}$$\end{document} contingency tables: A unified framework Journal of the American Statistical Association 100(471) 1009–1020 10.1198/016214504000002069CrossRefGoogle Scholar
Maydeu-Olivares, A., Joe, H., (2006). Limited and full information estimation and goodness-of-fit testing in multidimensional contingency tables Psychometrika 71 713–732 10.1007/s11336-005-1295-9CrossRefGoogle Scholar
Maydeu-Olivares, A., Liu, Y., (2012). Local dependence diagnostics in IRT modeling of binary data Educational and Psychological Measurement 73(2) 254–274Google Scholar
Maydeu-Olivares, A., Montaño, R., (2013). How should we assess the fit of Rasch-type models? Approximating the power of goodness-of-fit statistics in categorical data analysis Psychometrika 78 116–133 10.1007/s11336-012-9293-1 25107521CrossRefGoogle ScholarPubMed
Mirvaliev, M., (1987). The components of chi-squared statistics for goodness-of-fit tests Journal of Soviet Mathematics 38 2357–2363 10.1007/BF01095078CrossRefGoogle Scholar
National Institute of Mental Health (NIMH). (2019). Results from the 2017 national survey on drug use and mental health. https://www.samhsa.gov/data/sites/default/files/cbhsq-reports/NSDUHDetailedTabs2017/NSDUHDetailedTabs2017.htm#tab8-56A. Accessed 15 June 2020Google Scholar
Rayner, J. C. W., & Best, D. J. (1989). Smooth tests of goodness of fit. Oxford.Google Scholar
Reiser, M., (1989). An application of the item response model to psychiatric epidemiology Sociological Methods & Research 18 66–103 10.1177/0049124189018001003CrossRefGoogle Scholar
Reiser, M., (1996). Analysis of residuals for the multinomial item response model Psychometrika 61 509–528 10.1007/BF02294552CrossRefGoogle Scholar
Reiser, M., (2008). Goodness-of-fit testing using components based on marginal frequencies of multinomial data British Journal of Mathematical and Statistical Psychology 61(2) 331–360 10.1348/000711007X204215 17535483CrossRefGoogle ScholarPubMed
Reiser, M., (2019). Goodness-of-fit testing in sparse contingency tables when the number of variables is large WIRES Computational Statistics 11(6) e1470 10.1002/wics.1470CrossRefGoogle Scholar
Reiser, M., & Dassanayake, M. (2021). A study of lack-of-fit diagnostics for models fit to cross-classified binary variables. In Porzio, G. Rampichini, C. & Bocci, C. (Eds.), CLADAG 2021 book of abstracts and short papers (pp. 191–194). Firenze University Press. https://doi.org/10.36253/978-88=5518-340-6CrossRefGoogle Scholar
Salomaa, H. (1990). Factor analysis of dichotomous data. Statistical Society.Google Scholar
Schabenberger, O. (2005). Mixed model influence diagnostics. In SAS users group international conference (SUGI), 189-29.Google Scholar
Simonoff, J.S. (1986). Jackknifing and bootstrapping goodness-of-fit statistics in sparse multinomials. Journal of the American Statistical Association, 81(396), 1005–1011.CrossRefGoogle Scholar
Tollenaar, N., & Mooijaart, A. (2003). Type I errors and power of the parametric bootstrap goodness-of-fit test: Full and limited information. British Journal of Mathematical and Statistical Psycholgy, 56, 271–288.CrossRefGoogle Scholar
Sharma, S. (1995). Applied multivariate techniques. Wiley.Google Scholar
Verbeke, G., & Molenberghs, G. (2009). Linear mixed models for longitudinal data. Springer.Google Scholar
Yen, W., (1981). Using simulation results to choose a latent trait model Applied Psychological Measurement 5(2) 245–262 10.1177/014662168100500212CrossRefGoogle Scholar
Supplementary material: File

Reiser et al. supplementary material

Reiser et al. supplementary material 1
Download Reiser et al. supplementary material(File)
File 200.5 KB
Supplementary material: File

Reiser et al. supplementary material

Reiser et al. supplementary material 2
Download Reiser et al. supplementary material(File)
File 20.5 KB