Article contents
Generic Identifiability of the DINA Model and Blessing of Latent Dependence
Published online by Cambridge University Press: 01 January 2025
Abstract
Cognitive diagnostic models are a powerful family of fine-grained discrete latent variable models in psychometrics. Within this family, the DINA model is a fundamental and parsimonious one that has received significant attention. Similar to other complex latent variable models, identifiability is an important issue for CDMs, including the DINA model. Gu and Xu (Psychometrika 84(2):468–483, 2019) established the necessary and sufficient conditions for strict identifiability of the DINA model. Despite being the strongest possible notion of identifiability, strict identifiability may impose overly stringent requirements on designing the cognitive diagnostic tests. This work studies a slightly weaker yet very useful notion, generic identifiability, which means parameters are identifiable almost everywhere in the parameter space, excluding only a negligible subset of measure zero. We propose transparent generic identifiability conditions for the DINA model, relaxing existing conditions in nontrivial ways. Under generic identifiability, we also explicitly characterize the forms of the measure-zero sets where identifiability breaks down. In addition, we reveal an interesting blessing-of-latent-dependence phenomenon under DINA—that is, dependence between the latent attributes can restore identifiability under some otherwise unidentifiable Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$${\mathbf {Q}}$$\end{document}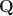 -matrix designs. The blessing of latent dependence provides useful practical implications and reassurance for real-world designs of cognitive diagnostic assessments.
-matrix designs. The blessing of latent dependence provides useful practical implications and reassurance for real-world designs of cognitive diagnostic assessments.
Keywords
- Type
- Theory and Methods
- Information
- Copyright
- Copyright © 2022 The Author(s) under exclusive licence to The Psychometric Society
Footnotes
Supplementary Information The online version contains supplementary material available at https://doi.org/10.1007/S0033312300006049.
References
- 2
- Cited by


