Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-28T02:40:31.977Z Has data issue: false hasContentIssue false
  • English
  • Français

Wavefunction Tails in the Modal Interpretation

Published online by Cambridge University Press:  28 February 2022

Michael Dickson
Michael Dickson*
Affiliation:
University of Notre Dame
Get access Rights & Permissions [Opens in a new window]

Extract

Consider the general form of the state of a quantum system, 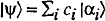(eq. 1), where the 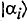are (non-degenerate) eigenvectors of an operator, A, corresponding to an observable, A. According to the standard interpretation of quantum mechanics (the precise details of which do not concern me here), A does not have a definite value on the system in the state 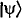. But now suppose we measure A by coupling the system to a measuring apparatus. The composite system is then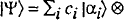 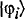(eq. 2) where the 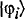are the indicator-states of the apparatus. Again, the standard interpretation tells us that the apparatus is not in a definite indicator-state. But how can this be? Measurements do have definite results. The apparatus is always in a definite state.

I have just reviewed one version of the measurement problem. The modal interpretation of quantum mechanics proposes a solution.

Type
Part IX. Quantum Mechanics: Decoherence and Related Matters
Information
PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association , Volume 1994 , Issue 1: Volume One: Contributed Papers 1994 , 1994 , pp. 366 - 376
Copyright
Copyright © 1994 by the Philosophy of Science Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Thanks to James Cushing for invaluable comments and discussion. Thanks also to Guido Bacciagaluppi, Dennis Dieks, and Meir Hemmo for their helpful remarks. Thanks to the University of Notre Dame and the Mellon Foundation for generous financial support while this work was being done.

References

Aharanov, Y., Anandan, J., and Vaidman, L. (1993), “Meaning of the Wave Function”, Physical Review A 47:4616–4626.CrossRefGoogle Scholar
Albert, D. and Loewer, B. (1990), “Wanted Dead or Alive: Two Attempts to Solve Schrödinger's Paradox”, in Fine, A., Forbes, M., and Wessels, E., (eds.), PSA 1990, vol. I. East Lansing, MI: Philosophy of Science Association.Google Scholar
Albert, D. and Loewer, B. (1991), “Some Alleged Solutions To the Measurement Problem”, Synthese 88:87–98.CrossRefGoogle Scholar
Albert, D. and Loewer, B. (1993), “Non-Ideal Measurements”, Foundations of Physics Letters 6:297–305.CrossRefGoogle Scholar
Bacciagaluppi, G., and Hemmo, M. (1994a), “Modal Interpretation of Imperfect Measurements”, University of Cambridge preprint.Google Scholar
Bacciagaluppi, G., and Hemmo, M. (1994b), “Making Sense of Approximate Decoherence”, this volume.CrossRefGoogle Scholar
Bohm, D. (1951) Quantum Theory. New York: Prentice-Hall.Google Scholar
Bub, J. (1992), “Quantum Mechanics Without the Projection Postulate”, Foundations of Physics 22:737–754.CrossRefGoogle Scholar
Bub, J. (1993), “Measurement: It Ain't Over Till It's Over”, Foundations of Physics Letters 6:21–35.CrossRefGoogle Scholar
Clifton, R. (1994), “Independently Motivating the Dieks-Kochen Modal Interpretation of Quantum Mechanics”, University of Western Ontario preprint.CrossRefGoogle Scholar
Cushing, J.T. (1975), Applied Analytical Mathematics for Physical Scientists. New York: John Wiley & Sons.Google Scholar
DeWitt, B. (1994), “How Does the Classical World Emerge From the Wave Function?”, in Mansouri, F. and Scanio, J.J., (eds.), Topics on Quantum Gravity and Beyond. Singapore: World Scientific.Google Scholar
Dieks, D. (1988), “The Formalism of Quantum Theory: An Objective Description of Reality?”, Annalen der Physik 7:174–190.CrossRefGoogle Scholar
Dieks, D. (1989), “Quantum Mechanics Without the Projection Postulate and Its Realistic Interpretation’, Foundations of Physics 19:1397–1423.CrossRefGoogle Scholar
Dieks, D. (1989), “Resolution of the Measurement Problem Through Decoherence of the Quantum State” Physics Letters A 142:439–446.CrossRefGoogle Scholar
Dieks, D. (forthcoming), “The Modal Interpretation of Quantum Mechanics, Measurements and Macroscopic Behavior”, Physical Review A.Google Scholar
Elby, A. (1993), “Why ‘Modal’ Interpretations of Quantum Mechanics Don't Solve the Measurement Problem”, Foundations of Physics Letters 6:5–19.CrossRefGoogle Scholar
Elby, A. (1994), “The “Decoherence” Approach to the Measurement Problem in Quantum Mechanics”, this volume.CrossRefGoogle Scholar
Gell-Mann, M. and Hartle, J. (1990), “Quantum Mechanics in the Light of Quantum Cosmology”, in Zurek, W., (ed.), Complexity, Entropy, and the Physics of Information. New York: Addison-Wesley.Google Scholar
Healey, R. (1989), The Philosophy of Quantum Mechanics: An Interactive Interpretation. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Healey, R. (1993a), “Measurement and Quantum Indeterminateness”, Foundations of Physics Letters 6:307–316.CrossRefGoogle Scholar
Healey, R. (1993b), “Why Error-Prone Quantum Measurements Have Outcomes”, Foundations of Physics Letters 6:37–54.CrossRefGoogle Scholar
Hemmo, M. (1993), “Review of R. Healey's The Philosophy of Quantum Mechanics: An Interactive Interpretation”, Foundations of Physics 23:1137–1145.CrossRefGoogle Scholar
Kochen, S. (1985), “A New Interpretation of Quantum Mechanics”, in Lahti, P. and Mittelstaedt, P., (eds.), Symposium on the Foundations of Modern Physics. Teaneck, NJ: World Scientific Publishing Co..Google Scholar
Reed, M. and Simon, B. (1979), Methods of Modern Mathematical Physics. San Diego, CA: Academic Press.Google Scholar
Schrödinger, E. (1935), “Discussion of Probability Relations Between Separated Systems”, Proceedings of the Cambridge Philosophical Society 31:555–563.CrossRefGoogle Scholar
van Fraassen, B. (1979), “Hidden Variables and the Modal Interpretation of Quantum Theory”, Synthese 42:155–165.CrossRefGoogle Scholar
van Fraassen, B. (1981), “A Modal Interpretation of Quantum Mechanics”, in Beltrametti, E. and van Fraassen, B., (eds.), Current Issues in Quantum Logic. New York: Plenum.Google Scholar
van Fraassen, B. (1991), Quantum Mechanics: An Empiricist View. Oxford: Clarendon Press.CrossRefGoogle Scholar
Zurek, W. (1993), “Preferred States, Predictability, Classicality, and the Environment-Induced Decoherence”, in Halliwell, J., (ed.), The Physical Origins of Time Asymmetry. Cambridge: Cambridge University Press.Google Scholar