Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T17:33:32.987Z Has data issue: false hasContentIssue false
  • English
  • Français

Tachyon Signals, Causal Paradoxes, and the Relativity of Simultaneity

Published online by Cambridge University Press:  28 February 2022

Steven F. Savitt
Steven F. Savitt*
Affiliation:
The University of British Columbia
Get access Rights & Permissions [Opens in a new window]

Extract

The basic equations of the Special Theory of Relativity (STR) imply that no massive particle travelling at a velocity less than the velocity of light in vacuo (call that ‘c’) can be accelerated to a velocity either equal to or greater than c. For instance, the total energy E of a particle is given by the formula

(1)

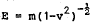
where m is the rest mass of the particle and v its velocity in some given co-ordinate system (CS). One can choose units so that c = 1; hence for ordinary particles (|v| < 1) as v approaches 1, E grows without bound. That is, as a particle accelerates, its total energy increases and ever-increasing amounts of energy are required to accelerate it. So no ordinary particle (tardyon, bradyon) can be accelerated continuously from velocity v < 1 to velocity v = 1, much less to velocity v > 1.

Type
Part VII. Tachyons, Temporal Becoming, and Thermodynamics
Information
PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association , Volume 1982 , Issue 1: Volume One: Contributed Papers 1982 , 1982 , pp. 277 - 292
Copyright
Copyright © Philosophy of Science Association 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

I have had help from Paul Fitzgerald, R.I.G. Hughes, Arthur Millman, Howard Pfeffer, and Tom Settle, to whom I extend my thanks.

References

Barashenkov, V.S. (1974). “Tachyons: Particles Moving with Velocities Greater than the Speed of Light.” Uspekhi Fiziohesklkh Nauk 114: 113–149. (English translation: Soviet Physics Uspekhi (1975) 17: 774-782.)Google Scholar
Bilaniuk, O.M.P. et al. (1962). “‘Meta’ Relativity.” American Journal of Physics 30: 718–723.CrossRefGoogle Scholar
Bilaniuk, O.M.P. and Sudarshan, E.C.G. (1969). “Particles Beyond the Light Barrier.” Phvsics Today 22(5): 43–51.CrossRefGoogle Scholar
Bilaniuk, O.M.P. and Sudarshan, E.C.G. et al. (1969). “More about Tachyons.” Physics Today 22(12): 47–52.CrossRefGoogle Scholar
Bohm, David. (1965). The Special Theory of Relativity. New York: W.A. Benjamin.Google Scholar
Earman, John. (1972). “Implications of Causal Propagation Outside the Null Cone.” Australasian Journal of Philosophy 50: 222–237.CrossRefGoogle Scholar
Feinberg, G. (1967). “Possibility of Faster-Than-Light Particles.” Physical Review 159: 1089–1105.CrossRefGoogle Scholar
Feinberg, G. (1970). “Particles that Go Faster Than Light.“ Scientific American 222(2): 69–77.CrossRefGoogle Scholar
Fitzgerald, Paul. (1971). “Tachyons, Backwards Causation, and Freedom.” In PSA 1970. (Boston Studies in the Philosophy of Science, Volume VIII.) Edited by Buck, R.C. and Cohen, R.S.. Dordrecht: Reidel. Pages 415–436.CrossRefGoogle Scholar
Maund, J.B. (1979). “Tachyons and Causal Paradoxes.” Foundations of Physics 9: 557–574.CrossRefGoogle Scholar
Newton, Roger G. (1967). “Causality Effects of Particles that Travel Faster than Light.” Physical Review 162: 1274.CrossRefGoogle Scholar
Newton, Roger G. (1970). “Particles that Travel Faster than Light.” Science 167: 1569–1574.CrossRefGoogle ScholarPubMed
Recami, Erasmo (ed.). (1978). Tachvons, Monopoles, and Related Subjects. Amsterdam: North Holland.Google Scholar
Rolnick, William B. (1969). “Implications of Causality for Fasterthan-Light Matter.” Physical Review 183: 1105–1108.CrossRefGoogle Scholar
Root, R.G. and Trefil, J.S. (1970). “An Amusing Paradox Involving Tachyons.” Letters al Nuovo Cimento 3: 412–414.CrossRefGoogle Scholar
Salmon, Wesley. (1975). Spacer Time, and Motion. Encino, California and Belmont, California: Dickenson Publishing Co., Inc.Google Scholar
Sudarshan, E.C.G. (1970). “The Theory of Particles Traveling Faster Than Light I.“ In Symposia on Theoretical Physios and Mathematics. Volume 10. Edited by Ramakishnan, Alladi. New York: Plenum Press. Pages 129-151.Google Scholar
Taylor, Edwin F. and Wheeler, John Archibald. (1966). Space time Physics. San Francisco: W.H. Freeman and Company.Google Scholar