Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T19:06:06.470Z Has data issue: false hasContentIssue false
  • English
  • Français

Probabilistic Causality, Randomization and Mixtures

Published online by Cambridge University Press:  31 January 2023

Jan von Plato
Jan von Plato*
Affiliation:
University of Helsinki
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The scheme of abstract dynamical systems will represent repetitive experimentation: There is a basic space of events X1 and the denumerable product 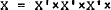… contains all possible sequences of events x = (x1, x2, … ). There are projections qn which give the nth member of x: qn (x) = xn. A transformation T is defined over X by the equation qn (Tx)= q n+1 (x). It removes the sequence by one step, T(x1 ,x2 ,…) = (x2 ,x3 ,…) and is known as the shift transformation. It comes as an abstraction of the dynamical transformations of classical theories. Here it represents the performance of ‘the next’ experiment.

Type
Part VII. Probability And Causality
Information
PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association , Volume 1986 , Issue 1: Volume One: Contributed Papers 1986 , 1986 , pp. 432 - 437
Copyright
Copyright © Philosophy of Science Association 1986

References

Cornfeld, I.P.; Fomin, S.V. and Sinai, Ya.G. (1982). Ergodic Theory. Berlin: Springer.CrossRefGoogle Scholar
Daneri, A.; Loinger, A. and Prosperi, G.M., (1963). “Quantum Theory of Measurement and Ergodicity Conditions.” Nuclear Physics 33: 297–319.CrossRefGoogle Scholar
de Finetti, B. (1937). “La prévision: ses lois logiques, ses sources subjectives.” Annales de l’Institut Henri Poincaré 7: 1–68.Google Scholar
de Finetti, B. (1938). “Sur la condition d’équivalence partielle.” Actualités Scientifiques et Industrielles 737: 5–18.Google Scholar
Feller, W. (1971). An Introduction to Probability Theory and Its Applications Volume II. 2nd ed. New York: Wiley.Google Scholar
von Plato, J. (1982). “The significance of the ergodic decomposition of stationary measures for the interpretation of probability.” Synthese 53: 419–432.CrossRefGoogle Scholar