Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Copeland, B.Jack
2004.
Hypercomputation: philosophical issues.
Theoretical Computer Science,
Vol. 317,
Issue. 1-3,
p.
251.
Durand-Lose, Jérôme
2005.
Machines, Computations, and Universality.
Vol. 3354,
Issue. ,
p.
176.
Aaronson, Scott
2005.
Guest Column: NP-complete problems and physical reality.
ACM SIGACT News,
Vol. 36,
Issue. 1,
p.
30.
Gruska, Jozef
2007.
A broader view on the limitations of information processing and communication by nature.
Natural Computing,
Vol. 6,
Issue. 2,
p.
75.
Arkoudas, Konstantine
2008.
Computation, hypercomputation, and physical science.
Journal of Applied Logic,
Vol. 6,
Issue. 4,
p.
461.
Fraser, Robert
and
Akl, Selim G.
2008.
Accelerating machines: a review.
International Journal of Parallel, Emergent and Distributed Systems,
Vol. 23,
Issue. 1,
p.
81.
Welch, Philip D.
2009.
Unconventional Computation.
Vol. 5715,
Issue. ,
p.
37.
Durand-Lose, Jérôme
2009.
Unconventional Computation.
Vol. 5715,
Issue. ,
p.
158.
Andréka, Hajnal
Németi, István
and
Németi, Péter
2009.
General relativistic hypercomputing and foundation of mathematics.
Natural Computing,
Vol. 8,
Issue. 3,
p.
499.
Button, Tim
2009.
Mathematical Theory and Computational Practice.
Vol. 5635,
Issue. ,
p.
68.
Durand-Lose, Jérôme
2009.
Abstract geometrical computation 3: black holes for classical and analog computing.
Natural Computing,
Vol. 8,
Issue. 3,
p.
455.
Durand-Lose, Jérôme
2011.
Abstract geometrical computation 5: embedding computable analysis.
Natural Computing,
Vol. 10,
Issue. 4,
p.
1261.
Jack Copeland, B.
and
Shagrir, Oron
2011.
Do Accelerating Turing Machines Compute the Uncomputable?.
Minds and Machines,
Vol. 21,
Issue. 2,
p.
221.
Minati, Gianfranco
and
Pessa, Eliano
2018.
From Collective Beings to Quasi-Systems.
p.
25.
Stacewicz, Paweł
2020.
Analogicity in Computer Science. Methodological Analysis.
Studies in Logic, Grammar and Rhetoric,
Vol. 63,
Issue. 1,
p.
69.
Copeland, B. Jack
and
Shagrir, Oron
2020.
Quantum, Probability, Logic.
p.
217.
Brauer, Ethan
2021.
The dependence of computability on numerical notations.
Synthese,
Vol. 198,
Issue. 11,
p.
10485.
Fiske, Michael Stephen
2021.
Advances in Software Engineering, Education, and e-Learning.
p.
375.
Boker, Udi
and
Dershowitz, Nachum
2022.
Axiomatic Thinking II.
p.
199.
Miguel-Tomé, Sergio
Sánchez-Lázaro, Ángel L.
and
Alonso-Romero, Luis
2022.
Fundamental Physics and Computation: The Computer-Theoretic Framework.
Universe,
Vol. 8,
Issue. 1,
p.
40.
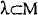 with past endpoint and a point q∊M such that
with past endpoint and a point q∊M such that 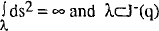 .
.