Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-27T11:22:18.425Z Has data issue: false hasContentIssue false
  • English
  • Français

I. Dynamical Reduction Theories: Changing Quantum Theory so the Statevector Represents Reality

Published online by Cambridge University Press:  31 January 2023

GianCarlo Ghirardi  and
Philip Pearle
GianCarlo Ghirardi
Affiliation:
University of Trieste and Hamilton College
Philip Pearle
Affiliation:
University of Trieste and Hamilton College
Get access Rights & Permissions [Opens in a new window]

Extract

We dedicate these papers to the memory of John Bell, whose contributions to, support for, and encouragement of the research program described here has meant more than words can say to those involved in it.

In Schrödinger’s “cat paradox” example, a nucleus which has a 50% probability of decaying within an hour is coupled to a cat by a “hellish contraption” which, if it detects the decay, will kill the cat. If we take the point of view that what we see around us is real, what occurs in reality is one of the two following evolutions :

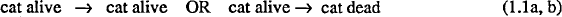
(—> means “evolves in an hour into“).

According to Schrödinger’s equation, the evolution of the statevector describing this situation is

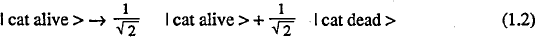
The right hand side of Eq. (1.2) does not correspond to either the reality on the right hand side of (1.1a) nor to the reality on the right hand side of (1.1b).

Type
Part II. John S. Bell Session: State Vector Reduction
Information
PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association , Volume 1990 , Issue 2: Volume Two: Symposia and Invited Papers 1990 , 1990 , pp. 19 - 33
Copyright
Copyright © Philosophy of Science Association 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

One of us (P.P.) would like to acknowledge the hospitality of Prof. Abdus Salam, the International Atomic Energy Agency and UNESCO, as well as financial support from Hamilton College, the Istituto Nazionale di Fisica Nucleare, and the Consorzio per l’Incremento degli Studi e delle Richerche in Fisica dell’Università di Trieste.

References

Aicardi, F., Borsellino, A., Ghirardi, G. C, and Grassi, R. (1991),“Dynamical Models For State-Vector Reduction: Do They Ensure That Measurements Have Outcomes?”, to be published in Foundations of Physics Letters.CrossRefGoogle Scholar
Belavkin, V. P. (1989), Physics Letters. 140: 355–358.CrossRefGoogle Scholar
Bell, J. S. (1987), Schrodinger-Centenary celebration of a polymath,.C. W., Kilmister (ed.). Cambridge: Cambridge University Press.Google Scholar
Bell, J. S. (1990), Sixty-Two Years of Uncertainty. Miller, A. (ed.). New York: Plenum, pp. 17–32.CrossRefGoogle Scholar
Benatti, F., Ghirardi, G., C.A., Rimini and Weber, T. (1986), Nuovo Ciment. 100B: 27–41.Google Scholar
Bohm, D. and Bub, J. (1966), Reviews of Modern Physic. 38:453–469.CrossRefGoogle Scholar
Diosi, L. (1988), Physics Letter. A 132: 233–236.CrossRefGoogle Scholar
Einstein, A. (1949), “Reply to Criticism” in Albert Einstein: Philosopher-Scientist. Schilpp, P.A. (ed.), LaSalle, Ill.: Open Court.Google Scholar
Feynman, R.P., Leighton, R.B. and Sands, M. (1965), The Feynman Lectures on Physics, Vol III. Mass: Addison Wesley, p.1–1.Google Scholar
Frenkel, A. (1990), Foundations of Physic. 20:159–188.CrossRefGoogle Scholar
Gatarek, D. and Gisin, N. (1990), “Continuous Quantum Jumps and Infinite-Dimensional Stochastic Equations”: preprint.Google Scholar
Ghirardi, G.C., Rimini, A. and Weber, T. (1985), Quantum Probability and Applications II. Accardi, L. and von Waldenfels, .W. (eds.). Berlin: Springe pp. 223–232.CrossRefGoogle Scholar
Ghirardi, G.C., Rimini, A. and Weber, T. (1986) Physical Review D34: 470–491.Google Scholar
Ghirardi, G.C., Rimini, A. and Weber, T. (1987), Physical Review D36: 3287–3289.Google Scholar
Ghirardi, G.C., Rimini, A. and Weber, T. (1988), Foundations of Physics 18:1–27.CrossRefGoogle Scholar
Ghirardi, G. C., Pearle, P. and Rimini, A. (1990), Physical Review A42:78–89.CrossRefGoogle Scholar
Ghirardi, G. C. and Rimini, A. (1990), Sixty-Two Years of Uncertainty., Miller, .A. (ed.). New York: Plenum, pp. 167–191.CrossRefGoogle Scholar
Ghirardi, G. C, Grassi, R. and Pearle, P. (1990a), Foundations of Physic. 20:1271–1316.CrossRefGoogle Scholar
Ghirardi, G. C, Grassi, R. and Pearle, P. (1990b), “Relativistic Dynamical Reduction Models and Locality”, to be published in the Proceedings of the Symposium on the Foundations of Modern Physics 1990. Lahti, P. and Mittelstaedt, P., (eds.). Singapore, World Scientific.Google Scholar
Gisin, N. (1984a), Physical Review Letter. 52:1657–1660.CrossRefGoogle Scholar
Gisin, N. (1984b), Physical Review Letter. 53:1776.CrossRefGoogle Scholar
Gisin, N. (1989), Helvetica Physica Ad. 62: 363–371.Google Scholar
Karolyhazy, F. (1966), Il Nuovo Ciment. 42A: 390-402.Google Scholar
Karolyhazy, F. (1990), Sixty-Two Years of Uncertainty. Miller, A. (ed.). New York: Plenum, pp. 215–231.CrossRefGoogle Scholar
Karolyhazy, E, Frenkel, A. and Lukacz, B. (1982), Physics as Natural Philosophy. Shimony, A. and Feshbach, H. (eds.). Cambridge: M.I.T., pp. 204–239.Google Scholar
Karolyhazy, E, Frenkel, A. and Lukacz, B. (1986), Quantum Concepts in Space and Time. Penrose, R. and Isham, C. J.(eds.). Oxford: Clarendon, pp.109–128.Google Scholar
Nicrosini, O. and Rimini, A. (1990), Foundations of Physic. 20:1317–1328.CrossRefGoogle Scholar
Pearle, P. (1976), Physical Review. D13:857–868.Google Scholar
Pearle, P. (1979), International Journal of Theoretical Physics. 48: 489–518.CrossRefGoogle Scholar
Pearle, P. (1982), Foundations of Physics 12: 249–263.CrossRefGoogle Scholar
Pearle, P. (1984a), Physical Review. D29: 235–240.Google Scholar
Pearle, P. (1984b), The Wave-Particle Dualism. Diner, S. et. al (eds.). Dordrecht: Reidel, pp. 457–483.CrossRefGoogle Scholar
Pearle, P. (1985), Journal of Statistical Physics. 41: 719–727.CrossRefGoogle Scholar
Pearle, P. (1986a), Quantum Concepts in Space and Time. Penrose, R. and Isham, C. J. (eds.). Oxford: Clarendon, pp. 84–108.Google Scholar
Pearle, P. (1986b), New Techniques in Quantum Measurement Theory., Greenberger, D. M. (ed.). New York: N.Y. Acad. of Sci., pp. 539–552.Google Scholar
Pearle, P. (1989), Physical Review. A39:2277–2289.CrossRefGoogle Scholar
Pearle, P. (1990), Sixty-Two Years of Uncertainty. Miller, A. (ed.). New York: Plenum, pp. 193–214.CrossRefGoogle Scholar
Penrose, R. (1986), Quantum Concepts in Space and Time. Penrose, R. and Isham, C. J. (eds.). Oxford: Clarendon, pp. 129–146.Google Scholar
Stapp, H. (1989), “Noise-Induced Reduction of Wave Packets”: preprint LBL-26968.Google Scholar
Zeilinger, A., Gaehler, R., Shull, C. G. and Treimer, .W. (1984), Symposium on Neutron Scattering. Faber, J. Jr. (ed.). New York: Amer. fast, of Phys.Google Scholar
Zeilinger, A. (1986), Quantum Concepts in Space and Time. Penrose, R. and Isham, C. J. (eds.). Oxford: Clarendon, pp. 16–27.Google Scholar