Published online by Cambridge University Press: 28 February 2022
According to de Finetti's representation theorem, probabilities of exchangeable sequences of events are unique mixtures of Bernoullian probabilities. The exchangeable probability P(E) of the sequence E equals an integral of the form 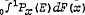 , where Px(E) is for each x (0≦x≦1) a Bernoullian measure with the probability x for ‘success’ and independence between consecutive events, and F a uniquely determined distribution of the parameter x. P(E) equals the expected value of Px(E). If F has a derivative f,
, where Px(E) is for each x (0≦x≦1) a Bernoullian measure with the probability x for ‘success’ and independence between consecutive events, and F a uniquely determined distribution of the parameter x. P(E) equals the expected value of Px(E). If F has a derivative f, 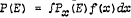 Probabilities can be calculated under the integral sign as if events were independent and had a constant success probability. Therefore there cannot be anything one can do with Bernoullian probabilities, but could not do with the exchangeable ones, de Finetti thinks that he has, because of the unique correspondence between exchangeable measures and distributions over a parameter each value of which gives a Bernoullian probability, shown the unnecessity of the latter.
Probabilities can be calculated under the integral sign as if events were independent and had a constant success probability. Therefore there cannot be anything one can do with Bernoullian probabilities, but could not do with the exchangeable ones, de Finetti thinks that he has, because of the unique correspondence between exchangeable measures and distributions over a parameter each value of which gives a Bernoullian probability, shown the unnecessity of the latter.