Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-27T18:22:26.214Z Has data issue: false hasContentIssue false
  • English
  • Français

The Extent of Dilation of Sets of Probabilities and the Asymptotics of Robust Bayesian Inference

Published online by Cambridge University Press:  28 February 2022

Timothy Herron ,
Teddy Seidenfeld  and
Larry Wasserman
Timothy Herron
Affiliation:
Carnegie-Mellon University
Teddy Seidenfeld
Affiliation:
Carnegie-Mellon University
Larry Wasserman
Affiliation:
Carnegie-Mellon University
Get access Rights & Permissions [Opens in a new window]

Extract

We discuss two general issues concerning diverging sets of Bayesian (conditional) probabilities—divergence of “posteriors”—that can result with increasing evidence. Consider a set 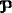of probabilities typically, but not always, based on a set of Bayesian “priors.” Incorporating sets of probabilities, rather than relying on a single probability, is a useful way to provide a rigorous mathematical framework for studying sensitivity and robustness in Classical and Bayesian inference. See: Berger (1984, 1985, 1990); Lavine (1991); Huber and Strassen (1973); Walley (1991); and Wasserman and Kadane (1990). Also, sets of probabilities arise in group decision problems. See: Levi (1982); and Seidenfeld, Kadane, and Schervish (1989). Third, sets of probabilities are one consequence of weakening traditional axioms for uncertainty. See: Good (1952); Smith (1961); Kyburg (1961); Levi (1974); Fishburn (1986); Seidenfeld, Schervish, and Kadane (1990); and Walley (1991).

Type
Part VII. Statistics and Experimental Reasoning
Information
PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association , Volume 1994 , Issue 1: Volume One: Contributed Papers 1994 , 1994 , pp. 250 - 259
Copyright
Copyright © 1994 by the Philosophy of Science Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Timothy Herron and Teddy Seidenfeld were supported by NSF grant SES-9208942. Larry Wasserman was supported by NSF Grant DMS-90005858, and NIH grant R01-CA54852-01.

References

Berger, J.O. (1984), “The Robust Bayesian Viewpoint”, with discussion, in Kadane, J.B., (ed.), Robustness of Bayesian Analysis Amsterdam: North-Holland, 63–144.Google Scholar
Berger, J.O. (1985), Statistical Decision Theory, (2nd edition). N. Y.: Springer-Verlag.Google Scholar
Berger, J.O. (1990), “Robust Bayesian analysis: sensitivity to the prior”, J. Stat. Planning & Inference 25: 303–328.CrossRefGoogle Scholar
Blackwell, D. & Dubins, L. (1962), “Merging of opinions with increasing information”, Ann. Math. Stat. 33: 882–887.CrossRefGoogle Scholar
DeRobertis, L. and Hartigan, J. A. (1981), “Bayesian inference using intervals of measures”, Annals of Statistics 9: 235–244.Google Scholar
Ellsberg, D. (1961), “Risk, Ambiguity, and the Savage Axioms”, Quart. J. Econ. 75: 643–669.CrossRefGoogle Scholar
Fishburn, P.C. (1986), “The Axioms of Subjective Probability”, Statistical Science 1:335–358.Google Scholar
Good, I.J. (1952), “Rational Decisions”, J. Royal Stat. Soc. B, 14: 107–114.Google Scholar
Herron, T., Seidenfeld, T., and Wasserman, L. (1993), “Divisive Conditioning”, Tech.Report #585, Dept. of Statistics, Carnegie Mellon University. Pgh., PA 15213.Google Scholar
Huber, P.J. (1973), “The use of Choquet capacities in statistics”, Bull. Inst. Int. Stat. 45:181–191.Google Scholar
Huber, P.J. (1981), Robust Statistics, New York: Wiley.CrossRefGoogle Scholar
Huber, P.J. and Strassen, V. (1973), “Minimax tests and the Neyman-Pearson lemma for capacities”, Annals of Statistics 1: 241–263.CrossRefGoogle Scholar
Jeffreys, H. (1967), Theory of Probability (3rd ed.), Oxford: Oxford University Press.Google Scholar
Kyburg, H.E. (1961), Probability and Logic of Rational Belief, Middleton, CT: Wesleyan Univ. Press.Google Scholar
Lavine, M. (1991), “Sensitivity in Bayesian statistics: the prior and the likelihood”, Journal of American Statistics Association 86: 396–399.CrossRefGoogle Scholar
Levi, I. (1974), “On indeterminate probabilities”, Journal of Philosophy 71: 391–418.CrossRefGoogle Scholar
Levi, I. (1982), “Conflict and Social Agency”, Journal ofPhilosophy 79: 231–247.CrossRefGoogle Scholar
Pericchi, L.R. and Walley, P. (1991), “Robust Bayesian Credible Intervals and Prior Ignorance”, Int. Stat. Review 58:1–23.CrossRefGoogle Scholar
Savage, L.J. (1954), The Foundations of Statistics, New York: Wiley.Google Scholar
Seidenfeld, T., Kadane, J.B., and Schervish, M.J. (1989), “On the shared preferences of two Bayesian decision makers”, Journal of Philosophy 86: 225–244.CrossRefGoogle Scholar
Seidenfeld, T, Schervish, M.J., and Kadane, J.B. (1990), “Decisions without Ordering”, in Sieg, W. (ed.), Acting and Reflecting, Dordrecht: Kluwer Academic, pp. 143–170.CrossRefGoogle Scholar
Seidenfeld, T. and Wasserman, L. (1993), “Dilation for sets of probabilities”, Annals of Statistics. 21: 1139–1154.CrossRefGoogle Scholar
Smith, C.A.B. (1961), “Consistency in statistical inference and decisions”, J. Royal Stat. Soc. B. 23: 1–25.Google Scholar
Walley, P. (1991), Statistical Reasoning with Imprecise Probabilities, London: Chapman Hall.CrossRefGoogle Scholar
Wasserman, L. and Kadane, J.B. (1990), “Bayes’ theorem for Choquet capacities”, Annals of Statistics 18: 1328–1339.CrossRefGoogle Scholar