Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T19:45:48.026Z Has data issue: false hasContentIssue false
  • English
  • Français

Where the Theory of Probability Fails

Published online by Cambridge University Press:  28 February 2022

Itamar Pitowsky
Itamar Pitowsky*
Affiliation:
Philosophy Department, The University of Western Ontario
Get access Rights & Permissions [Opens in a new window]

Extract

The purpose of this paper is to present a local solution to the Einstein-Rosen-Podolsky (E.P.R.) paradox by way of a mechanical analogue (roulette) and then to note some of its consequences for the foundations of mathematics and probability theory. The detailed mathematical development of the model involves some highly specialized fields in mathematics (set theory, measure theory and group theory). My intention is to avoid these technicalities as much as possible. A complete account that includes proofs and application to physics is in Pitowsky (1982a, 1982b, 1983). Some mathematics is, however, indispensable. I shall denote by x,y,z,w unit vectors in the three dimensional Euclidean Space. If x,y are unit vectors, 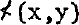is the (small) angle between x and y so that 0 ≤ 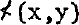≤ Π.

Type
Part XIV. Quantum Mechanics and Locality
Information
PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association , Volume 1982 , Issue 2: Volume Two: Symposia and Invited Papers 1982 , 1982 , pp. 616 - 623
Copyright
Copyright © 1983 Philosophy of Science Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Pitowsky, I. (1982a). “Resolution of the Einstein-Podolsky-Rosen and Bell Paradoxes.” Physical Review Letters 48: 1299-1302.CrossRefGoogle Scholar
Pitowsky, I. (1982b). “Answer to Comments.” Physical Review Letters 49: 1216.CrossRefGoogle Scholar
Pitowsky, I. (1983). “Deterministic Model of Spin and Statistics.” Physical Review D 27: 2316-2326.CrossRefGoogle Scholar
Quine, W.V.O. (1951). “Two Dogmas of Empiricism.” The Philosophical Review 60: 20-43. (As reprinted in From a Logical Point of View. New York: Harper & Row, 1961. Pages 20-46.Google Scholar
Solovey, R.H (1970). “A Model of Set Theory in Which Every Set of the Reals is Lebesgue Measurable.” Annals of Mathematics 92: 1-56.CrossRefGoogle Scholar