Introduction
The main functions of the seed coat are to protect the embryo and interact with the environment. The seed adjusts the germination process with the seasons in a way to make it compatible with a successful life cycle for the plant. The particular shape of the seed is an important factor for germination, as discussed in a paper studying the evolutionary role of seed shapes and volumes from 383 plant species from an alpine meadow on the eastern Qinghai–Tibet plateau (Bu et al., Reference Bu, Wang, Zhou, Qi, Liu, Ge, Dang-Hui and Zhang2016). The authors showed, for instance, that elongated and large seeds revealed faster speed of germination than small and round ones, while germinability was higher in smaller seeds when compared to larger ones (Bu et al., Reference Bu, Wang, Zhou, Qi, Liu, Ge, Dang-Hui and Zhang2016).
The germination process is controlled by a combination of biochemical factors (Carrera-Castaño et al., Reference Carrera-Castaño, Calleja-Cabrera, Pernas, Gómez and Oñate-Sánchez2020) and biomechanical properties (Steinbrecher and Leubner-Metzger, Reference Steinbrecher and Leubner-Metzger2017) of the seed. The molecular mechanisms and the genetic factors involved in seed germination were explored extensively in the past, as reviewed in Carrera-Castaño et al. (Reference Carrera-Castaño, Calleja-Cabrera, Pernas, Gómez and Oñate-Sánchez2020). Water intake activates several biochemical processes related to respiration, energy metabolism, and protein synthesis that facilitate the germination process through the elongation of the embryonic axis and the weakening of the endosperm. The correlation between the structural features of plant seeds and their function was investigated in a variety of plants (Gargiulo et al., Reference Gargiulo, Sorrentino and Mele2020; Kunishima et al., Reference Kunishima, Takeda, Hirose, Kalasová, Šalplachta and Omote2020), but the interplay between structure and mechanics during germination is less studied (Steinbrecher and Leubner-Metzger, Reference Steinbrecher and Leubner-Metzger2018).
The seeds of tobacco, Nicotiana tabacum L. (Solanaceae), a widely used model for germination (Koornneef et al., Reference Koornneef, Bentsink and Hilhorst2002; Manz et al., Reference Manz, Muller, Kucera, Volke and Leubner-Metzger2005), are covered by a coat composed by an outer layer of dead cells and an inner living part enclosing five layers of endosperm cells which surround the embryo (Koornneef et al., Reference Koornneef, Bentsink and Hilhorst2002; Manz et al., Reference Manz, Muller, Kucera, Volke and Leubner-Metzger2005). The process of germination in tobacco seed is due to embryo expansion that is driven by water uptake and the loosening of the endosperm cell wall which enable its deformation (Manz et al., Reference Manz, Muller, Kucera, Volke and Leubner-Metzger2005). Expansion of the embryo and endosperm lead to the rupture of the coat which is then followed by the rupture of the endosperm and the emergence of the radicle tip. Spatio-temporal analysis of nuclear magnetic resonance imaging of water uptake during germination shows that water distribution is heterogeneous: Water enters predominantly through the micropyle, as shown by the highest hydratation revealed in the micropylar region (Manz et al., Reference Manz, Muller, Kucera, Volke and Leubner-Metzger2005). A heterogeneous hydration pattern is observed throughout the entire germination process and remains observable until the final rupture of the endosperm (Manz et al., Reference Manz, Muller, Kucera, Volke and Leubner-Metzger2005).
The coat of tobacco seeds displays a characteristic puzzle-shaped cell structure (Cisneros et al., Reference Cisneros, Ghoshroy and Ghoshroy2011), a cellular pattern that is often observed and studied in plant leaves (Carter et al., Reference Carter, Sánchez-Corrales, Hartley, Grieneisen and Marée2017; Sapala et al., Reference Sapala, Runions, Routier-Kierzkowska, Gupta, Hong, Hofhuis, Verger, Mosca, Li, Hay, Hamant, AHK, Tsiantis, Prusinkiewicz and Smith2018, Reference Sapala, Runions and Smith2019; Lin and Yang, Reference Lin and Yang2020), in millet (Panicum miliaceum L.) seeds (Hasseldine et al., Reference Hasseldine, Gao, Collins, Jung, Jang, Song and Li2017), and in cells from the walnut (Juglans regia L.) (Antreich et al., Reference Antreich, Xiao, Huss, Horbelt, Eder, Weinkamer and Gierlinger2019) and other nut shells (Huss et al., Reference Huss, Antreich, Bachmayr, Xiao, Eder, Konnerth and Gierlinger2020). The intriguing character of puzzle-shaped cells was noticed already by D’Arcy Thompson in his pioneering book ‘On growth and form’ (Thompson, Reference Thompson1942). D’Arcy Thompson related the overwhelmingly hexagonal patterns observed in tissue cells to their mechanical properties through the minimisation of surface tension, with puzzle-shaped cells representing one of the few exceptions to this general observation. A paper used a computational model to show that puzzle-shaped cells in leaf provide a way to reduce mechanical stress in cell walls, maintaining structural integrity during leaf growth (Sapala et al., Reference Sapala, Runions, Routier-Kierzkowska, Gupta, Hong, Hofhuis, Verger, Mosca, Li, Hay, Hamant, AHK, Tsiantis, Prusinkiewicz and Smith2018). The mechanical role of puzzle-shaped cells was investigated experimentally and computationally in Panicum miliaceum seeds where it was shown that the coat structure was important in load transmission and redistribution under compression (Hasseldine et al., Reference Hasseldine, Gao, Collins, Jung, Jang, Song and Li2017).
Here, we analyse the germination process of tobacco seeds focusing on the role of puzzle-shaped cells in the mechanical properties of the seed coat. To this end, we perform scanning electron microscopy (SEM) imaging of tobacco seeds with intact or ruptured (e.g. after compression or germination) coats, digital image analysis of tobacco seed germination time-lapse recordings, and fracture tests of tobacco seeds as a function of their hydration state. Finally, we perform finite element analysis on simple, tobacco seed coat inspired structures, equivalent to metamaterials or architectured materials (Ashby, Reference Ashby2013; La Porta et al., Reference La Porta, Lionetti, Bonfanti, Milan, Ferrario, Rayneau-Kirkhope, Beretta, Hanifpour, Fascio and Ascagni2019; Rayneau-Kirkhope et al., Reference Rayneau-Kirkhope, Bonfanti and Zapperi2019), to investigate the mechanical role of the puzzle-shaped cell structure.
Materials and methods
Plant material, culture conditions, and germination
Nicotiana tabacum L. (Solanaceae) seeds were harvested in the autumn of 2018 from healthy plants cultivated at ‘Città Studi’ Botanical Garden (Milan, Italy) and were stored in a dry, dark place at room temperature (RT) for subsequent experiments. N. tabacum seeds were sterilised in a solution of 5% NaClO for 15 minutes and washed twice in distilled water, and left to dry for at least 1 hour under a chemical hood immediately before the experiments. For germination experiments, N. tabacum seeds were placed in a 35 mm petri dish containing phytagel medium. A solution containing 332.2 mg/ml CaCl
![]() $_2$
, 180.7 mg/ml MgSO
$_2$
, 180.7 mg/ml MgSO
![]() $_4$
, and 2% sucrose in distilled water was prepared and sterilised by filtration and kept at RT. Immediately before the experiment, the solution was diluted in distilled sterile water at RT and phytagel (P8169, Sigma-Aldrich, St. Louis, MO, USA) was added at a final concentration of 0.4%. Solution was heated up under rapid stirring until it clarified. Three millilitre of clarified solution were immediately added to each 35 mm Petri dish and let cool down at RT for about 15 minutes until the gel surface solidified. Sterilised seeds were placed on phytagel and images of germination were immediately acquired using a stereo-microscope (S9, Leica, Wetzlar, Germany) with camera at one frame per minute.
$_4$
, and 2% sucrose in distilled water was prepared and sterilised by filtration and kept at RT. Immediately before the experiment, the solution was diluted in distilled sterile water at RT and phytagel (P8169, Sigma-Aldrich, St. Louis, MO, USA) was added at a final concentration of 0.4%. Solution was heated up under rapid stirring until it clarified. Three millilitre of clarified solution were immediately added to each 35 mm Petri dish and let cool down at RT for about 15 minutes until the gel surface solidified. Sterilised seeds were placed on phytagel and images of germination were immediately acquired using a stereo-microscope (S9, Leica, Wetzlar, Germany) with camera at one frame per minute.
Seed deformation analysis
Digital analysis of seeds deformation was performed using an algorithm for particle image velocimetry (PIV). The algorithm compares intensity maps of two different frames and computes displacement vectors between them. For this purpose, we used PIVlab for MATLAB (Thielicke and Sonntag, Reference Thielicke and Sonntag2021) (https://pivlab.blogspot.com/). The displacements were identified by comparing frames at each time step with the frame at time zero. Displacements were assigned to grid points in space. Average displacement over time was then computed. For this analysis, we only considered two-dimensional images, so that only displacements projected on a plane could be measured. We analyse time-lapse images of three different seeds with a frame rate of one frame per minute.
Compression tests
Compression tests of tobacco seeds were carried out with accurate linear Dynamic Mechanical Analysis equipment DMA (mod. Q800, TA instruments, New Castle, DE, USA) at RT. Selected seeds of slightly elongated shape with axial dimensions of 0.5–0.8 mm were positioned on flat sample holders and compressed under controlled force mode at rate of 0.25 N/min up to complete collapse, after which the acquisition was stopped. We perform tests on four dry seeds and five seeds that had been kept for 48 hours in phytagel. The stiffness of the seed was computed performing a linear fit in the linear part of the deformation curve. Sampling rate was 2 points per second. We estimated the stiffness of the seeds by fitting a line to the curves in the initial elastic regime, for displacements smaller than
![]() $0.05$
mm. The linear regime was always followed by a regime of constant force, corresponding to the rupture force
$0.05$
mm. The linear regime was always followed by a regime of constant force, corresponding to the rupture force
![]() $F_c$
.
$F_c$
.
Scanning electron microscopy analysis
For fractured tobacco seeds, we performed fixation in 2% glutaraldehyde in 0.1 M cacodylate buffer for 2 hours, post-fixation in 1% osmium tetroxide for 2 hours, dehydration in increasing concentrations of ethanol (30 minutes each washing) and hexamethyldisilazane (HMDS)/absolute ethanol washings (1:3, 1:1, 3:1, 100% HMDS) for complete dehydration. The seeds were then gold-coated (Agar SEM Auto Sputter, Stansted, UK), fixed on the stub with conductive tape and directly observed under a scanning electron microscope (LEO-1430, Zeiss, Oberkochen, Germany). Secondary electron (SE) images were acquired at different magnifications with an operating voltage of 20 kV. Intact tobacco seeds were instead prepared for SEM analysis without performing fixation, post-fixation, and dehydration steps. Samples were gold-coated and observed as described above. The internal inspection of the seeds was achieved by cutting them in two halves and processing the halves with the same protocol cited above.
Statistical analysis
Statistical significance in seed stiffness and rupture force for dry and hydrated seeds is established by employing the Student’s t-test.
Design of the structures for computer simulations
The geometry of the model is defined by nodes that are necessary for creating the beams (segments) of the metamaterial. Every node is specified by its (
![]() $x,y,z$
) coordinates that refer to the origin of the global coordinate system. First, we define an initial configuration, placing randomly 100 principal nodes on the surface of a three-dimensional (3D) sphere of radius 1. Then we compute Voronoi’s diagram and connect the nodes obtaining several polygons (or cells) lying on the surface of the sphere. In order to generate puzzle-shaped cells, which are cells with curved beams, we transform the straight line connecting each pair of principal nodes of the polygons into a wavy segment introducing secondary nodes.
$x,y,z$
) coordinates that refer to the origin of the global coordinate system. First, we define an initial configuration, placing randomly 100 principal nodes on the surface of a three-dimensional (3D) sphere of radius 1. Then we compute Voronoi’s diagram and connect the nodes obtaining several polygons (or cells) lying on the surface of the sphere. In order to generate puzzle-shaped cells, which are cells with curved beams, we transform the straight line connecting each pair of principal nodes of the polygons into a wavy segment introducing secondary nodes.
Considering, for example, two connected principal nodes,
![]() $\mathbf {r}_A= (x_A,y_A, z_A)$
and
$\mathbf {r}_A= (x_A,y_A, z_A)$
and
![]() $\mathbf {r}_B=(x_B,y_B, z_B)$
, we can define the distance between two nodes as
$\mathbf {r}_B=(x_B,y_B, z_B)$
, we can define the distance between two nodes as
We then define a unit vector
![]() $\mathbf {e}$
pointing to the tangential direction:
$\mathbf {e}$
pointing to the tangential direction:
Afterwards, we introduce extra
![]() $N_p$
secondary nodes specified by (
$N_p$
secondary nodes specified by (
![]() $k = 1,2,\ldots ,N_p-1$
) in the A–B segment, that we define
$k = 1,2,\ldots ,N_p-1$
) in the A–B segment, that we define
 $$ \begin{align} \mathbf{n}_k:=(\mathbf{r}_B-\mathbf{r}_A) \frac{k}{N_p}, \end{align} $$
$$ \begin{align} \mathbf{n}_k:=(\mathbf{r}_B-\mathbf{r}_A) \frac{k}{N_p}, \end{align} $$
where
![]() $N_p$
is a chosen integer number, whose value is specified in the following.
$N_p$
is a chosen integer number, whose value is specified in the following.
The curvature in the segment is obtained through the calculation of the quantity
![]() $ \mathbf {e} A \sin \left ( \frac {\pi m k}{N_p}\right ) $
, where A is the amplitude of the curvature, and
$ \mathbf {e} A \sin \left ( \frac {\pi m k}{N_p}\right ) $
, where A is the amplitude of the curvature, and
![]() $m=(1,2,3,\ldots )$
is the number of waves along a segment.
$m=(1,2,3,\ldots )$
is the number of waves along a segment.
The final equation to get the positions of the secondary nodes tracing a wavy segments is
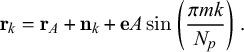 $$ \begin{align} \mathbf{r}_k=\mathbf{r}_A+\mathbf{n}_k + \mathbf{e} A \sin \left( \frac{\pi m k}{N_p}\right). \end{align} $$
$$ \begin{align} \mathbf{r}_k=\mathbf{r}_A+\mathbf{n}_k + \mathbf{e} A \sin \left( \frac{\pi m k}{N_p}\right). \end{align} $$
To control the shape of the wave, we can fine-tune three parameters:
-
• A: Amplitude of wave,
-
• m: Number of waves along a segment,
-
•
 $N_p$
: Number of discretization nodes.
$N_p$
: Number of discretization nodes.
Our 3D metamaterial with puzzle-shaped cells is obtained using
![]() $N_p = 100$
and setting different number of waves and amplitude according to the distance L between two principal nodes, for example,
$N_p = 100$
and setting different number of waves and amplitude according to the distance L between two principal nodes, for example,
![]() $\mathbf {r}_A$
and
$\mathbf {r}_A$
and
![]() $\mathbf {r}_B$
. For the case reported in Figure 5, we choose:
$\mathbf {r}_B$
. For the case reported in Figure 5, we choose:
-
• if
 $L<0.2$
:
$L<0.2$
:
 $m=3$
,
$m=3$
,
 $A=0.01$
;
$A=0.01$
; -
• if
 $0.2< L <0.4$
:
$0.2< L <0.4$
:
 $m=7$
,
$m=7$
,
 $A=0.03$
;
$A=0.03$
; -
• if
 $L>0.4$
:
$L>0.4$
:
 $m=9$
,
$m=9$
,
 $A=0.02$
.
$A=0.02$
.
Other parameters can be used according to the specific need and, furthermore, the number of starting nodes for the Voronoi sphere can be increased or decreased.
We modify Equation (4) introducing a Gaussian in order to smooth waves in the vicinity of the principal nodes avoiding overlaps or crossing of waves which can be problematic in finite element simulations. Specifically, we substitute the term
![]() $\sin \left ( \frac {\pi m k}{N_p}\right )$
with
$\sin \left ( \frac {\pi m k}{N_p}\right )$
with
 $$ \begin{align} \exp \left[ - \frac{ \left( \frac{\pi m k}{N_p} - \frac{\pi m}{2} \right)^2} {2 \sigma^2} \right] \cdot \sin \left( \frac{\pi m k}{N_p}\right), \end{align} $$
$$ \begin{align} \exp \left[ - \frac{ \left( \frac{\pi m k}{N_p} - \frac{\pi m}{2} \right)^2} {2 \sigma^2} \right] \cdot \sin \left( \frac{\pi m k}{N_p}\right), \end{align} $$
where, for example,
![]() $\sigma =\pi k/4$
.
$\sigma =\pi k/4$
.
The ellipsoidal shape that mimic the seed is obtained by transforming the initial sphere by means of directional scaling. In order to recreate the shape of the seed, we transform the nodes of the sphere into an ellipsoid, taking care of the experimental ratio between the longitudinal and lateral axes which is 1.25.
Finite element calculations
To reduce the computational cost of the calculation, we consider a small number of Voronoi centers, equal to 56 and 75 connections. With the use of Pymesh (a Geometry Processing Library for Python; https://pymesh.readthedocs.io/en/latest/#), we transform the point-like coordinates and links into a mesh of nodes connected with beams using the function WireNetwork and assign some thickness to the mesh using the Inflator function (inflator factor is 0.2). The mesh created with Pymesh is then imported into a finite element simulation program to perform tensile tests. The Finite Element Simulations are performed with COMSOL Multiphysics 5.3 using the solid mechanics module (https://www.comsol.com/comsol-multiphysics). Linear stress–strain relation were assumed for the constituent material and the mesh refinement analysis is adopted to ensure proper convergence.
In order to capture the properties of the wave network, we compare the net with wavy edges with the correspondent one with straight edges: The Voronoi nodes are placed in the same position (see Figure 2). We impose a displacement along the longitudinal y-direction at two endcaps of the net by freezing these regions. A quasi-static simulation is performed measuring the deformation of the net at each simulation step. The direction of the imposed displacement evolves throughout the simulation such that it is always along y. All studies assume a linear elastic material with Young’s modulus (
![]() $E=50$
MPa) and Poisson’s ratio (
$E=50$
MPa) and Poisson’s ratio (
![]() $\nu =0.3$
) which correspond approximately to experimentally measured values for seeds (Steinbrecher and Leubner-Metzger, Reference Steinbrecher and Leubner-Metzger2017). The total dimension of the seed is equal to
$\nu =0.3$
) which correspond approximately to experimentally measured values for seeds (Steinbrecher and Leubner-Metzger, Reference Steinbrecher and Leubner-Metzger2017). The total dimension of the seed is equal to
![]() $2,000\mu $
m
$2,000\mu $
m
![]() $\times\ 2,500\mu $
m
$\times\ 2,500\mu $
m
![]() $\times\ 2,000\mu $
m.
$\times\ 2,000\mu $
m.
Results
We analysed the structure of N. tabacum seeds using SEM. In Figure 1a, we display a typical image of a tobacco seed showing the characteristic pattern of puzzle-shaped cells on its coat. These puzzle-shaped cells displayed an elongated shape with an average maximum length of about 150–180
![]() $\mu $
m and anticlinal borders 8–13
$\mu $
m and anticlinal borders 8–13
![]() $\mu $
m high. The long axis of the cells is mainly oriented towards the germination point where their surfaces are drastically reduced. After 48-hour hydration, the cells slightly increased their surfaces and the anticlinal borders appeared to be slightly lower (Figure 1b).
$\mu $
m high. The long axis of the cells is mainly oriented towards the germination point where their surfaces are drastically reduced. After 48-hour hydration, the cells slightly increased their surfaces and the anticlinal borders appeared to be slightly lower (Figure 1b).
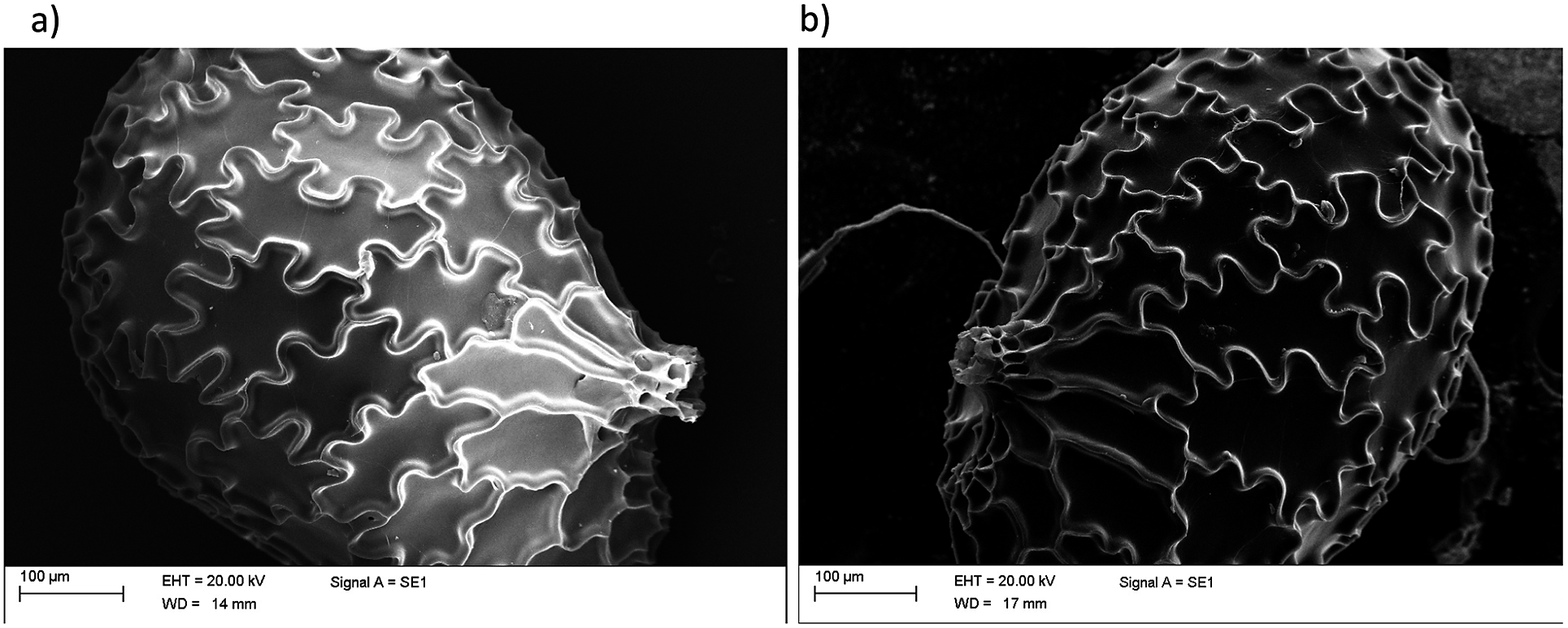
Figure 1. Scanning electron micrographs of dry and hydrated N. tabacum seeds. Image of typical intact seeds, displaying the characteristic puzzle-shape cells. (a) Dry seed. (b) Seed hydrated for 48 hours.
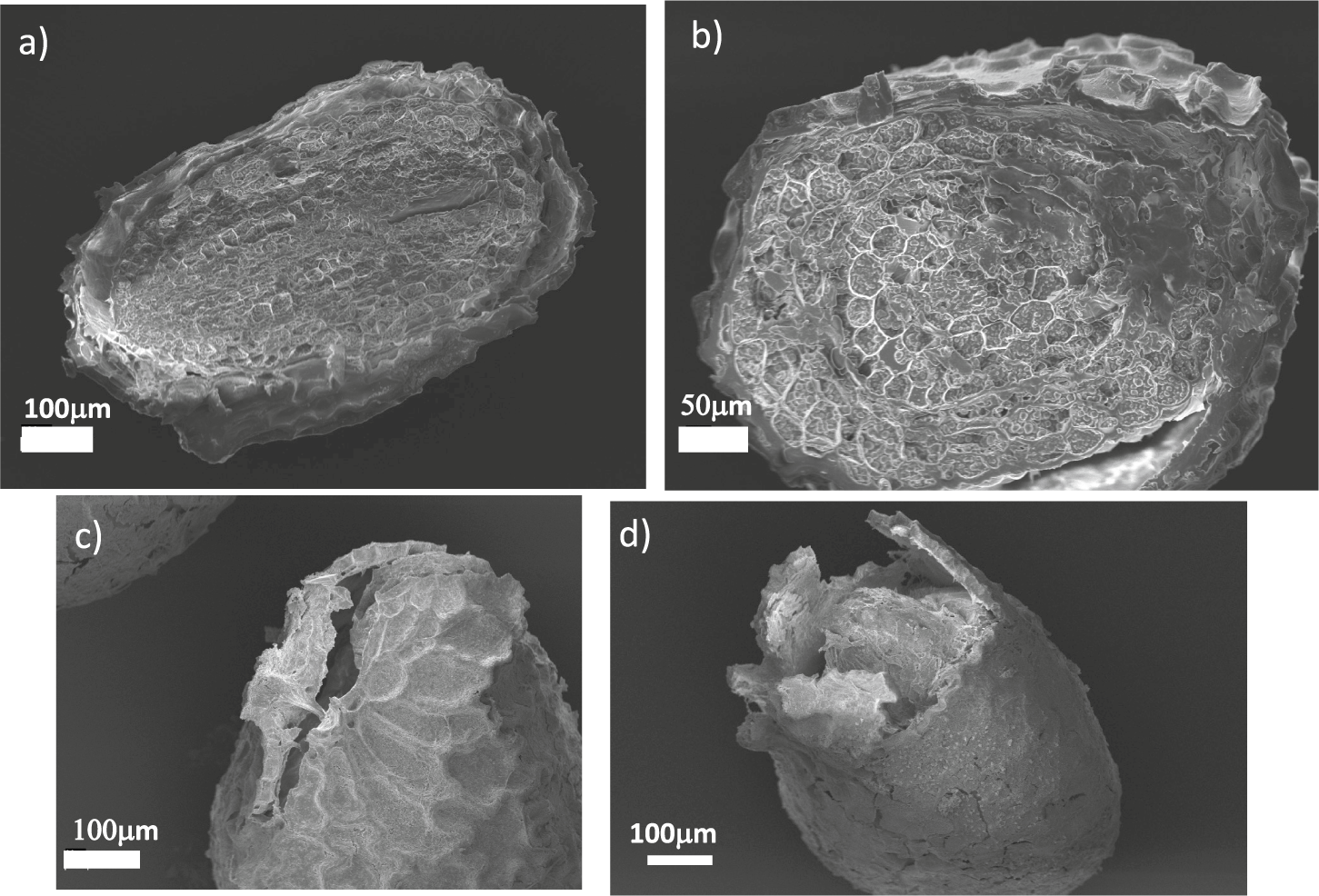
Figure 2. Scanning electron micrographs of sectioned and germinated N. tabacum seeds. (a) Longitudinal and (b) cross-sectional sections N. tabacum seeds revealing their internal structure. (c,d) Seeds after germination when the coat is ruptured.
The internal structure of the seed is illustrated in Figure 2a,b, where we report a SEM micrograph of a sectioned seed, showing a partial separation between the coat and the endosperm. From the image, we could estimate that the coat thickness was approximately 10
![]() $\mu $
m. Figure 2c,d displays the structure of the seed coats ruptured due to germination, showing that the fracture localised in the micropylar region. This localisation was observed in all our experiments and is in agreement with previous experimental observations (Manz et al., Reference Manz, Muller, Kucera, Volke and Leubner-Metzger2005). As already discussed, the micropylar region is the main entry point of water and is therefore more hydrated, leading to increased softening which is responsible for fracture localisation.
$\mu $
m. Figure 2c,d displays the structure of the seed coats ruptured due to germination, showing that the fracture localised in the micropylar region. This localisation was observed in all our experiments and is in agreement with previous experimental observations (Manz et al., Reference Manz, Muller, Kucera, Volke and Leubner-Metzger2005). As already discussed, the micropylar region is the main entry point of water and is therefore more hydrated, leading to increased softening which is responsible for fracture localisation.
To better characterise the deformation patterns leading to the rupture of the coat, we performed time-lapse observations of the germination process using a stereo-microscope. Performing three-dimensional microscopy of live seeds is challenging from the experimental point of view. To this end, researchers have used X-ray microscopy with phase contrast computed tomography (Kunishima et al., Reference Kunishima, Takeda, Hirose, Kalasová, Šalplachta and Omote2020) or multiple cameras mounted on robotized systems (Roussel et al., Reference Roussel, Geiger, Fischbach, Jahnke and Scharr2016). Since the seed shapes are approximately rotationally symmetric, a two-dimensional image provided relevant information. A typical example of the images we considered is reported in Figure 3a (see also Supplementary Movies S1–S3). We employed particle image velocimetry analysis to obtain the local displacement vectors induced by the germination process on the seed coat. The time-dependent functional form of the average displacement of the seed differed from seed to seed, as shown in Figure 3b, which reports three examples of these average displacement evolution curves during the final stages of germination. By observing in more details the displacement patterns on the coat surface, we noticed that in the initial stages of germination displacement vectors were small and uniformly distributed over the coat surface (see the first panel of Figure 3c). After a few minutes, however, the displacement fields started progressively orienting in the direction of the micropylar region, culminating in the localised rupture of the coat (Figure 3c and Supplementary Movie S4).
Figure 3. Deformation of germinating N. tabacum seeds. (a) A seed imaged under a stereo-microscope. (b) Average displacement as a function of time for the last part of the deformation curve for three different tobacco seeds. The zero of the time axis correspond to the time at which some deformation starts to be observable, and typically corresponds to 48 hours after hydration starts. (c) Displacement maps for a germinating seed obtained at different times through particle image velocimetry. The images correspond to seed 3 in panel (b).
To quantify the mechanical properties of tobacco seeds as a function of their hydration status, we performed compression tests (see Figure 4a). We considered two sets of seeds, a set of four dry seeds and a set of five seeds that had been previously hydrated for 48 hours. The force–displacement curves measured during the compression tests are reported in Figure 4b. The curves display an initial elastic regime, followed by a collapse plateau where the force did not increase and a final densification regime where the force increased non-linearly with the displacement. By fitting a line to the curves in the elastic regime (Figure 4c), we estimated the stiffness of the seeds. As shown in Figure 4d, seeds that are hydrated for 48 hours displayed a statistically significant reduction of the stiffness. The value of the force plateau, which corresponds to the force at which the coat ruptured, was also reduced for hydrated seeds with respect to dry seeds. In particular, the rupture force was
![]() $F_c=0.82 \pm 0.05$
N for dry seeds and
$F_c=0.82 \pm 0.05$
N for dry seeds and
![]() $F_c=0.50 \pm 0.10$
N for hydrated seeds. The difference was statistically significant (
$F_c=0.50 \pm 0.10$
N for hydrated seeds. The difference was statistically significant (
![]() $p<0.05$
). The weakening of the seed with hydration confirms the general idea that seed coat rupture during germination is helped by water-driven cell wall loosening (Manz et al., Reference Manz, Muller, Kucera, Volke and Leubner-Metzger2005). Examples of ruptured seeds observed with the SEM are reported in Figure 4d,e.
$p<0.05$
). The weakening of the seed with hydration confirms the general idea that seed coat rupture during germination is helped by water-driven cell wall loosening (Manz et al., Reference Manz, Muller, Kucera, Volke and Leubner-Metzger2005). Examples of ruptured seeds observed with the SEM are reported in Figure 4d,e.
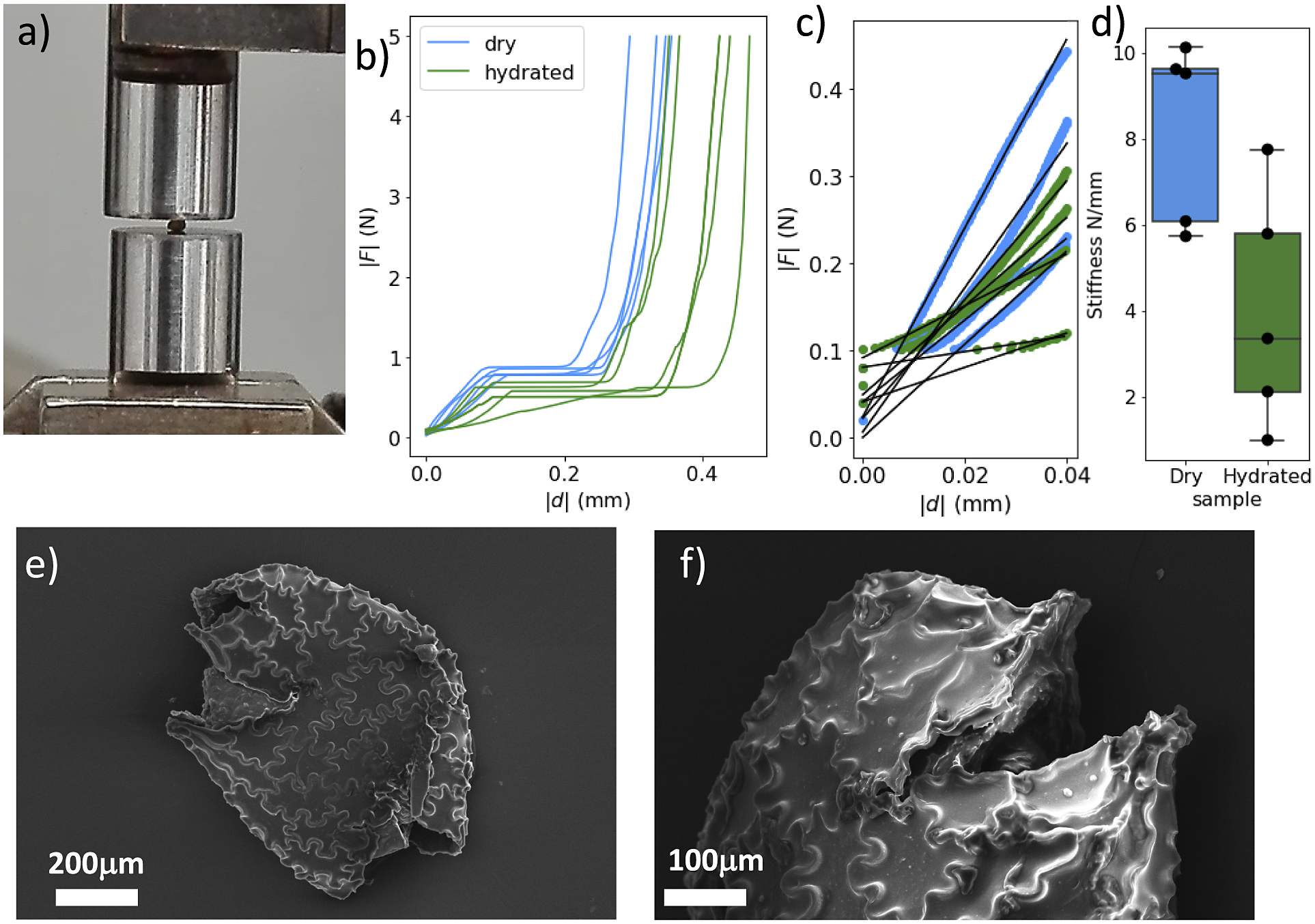
Figure 4.
Fracture of compressed N. tabacum seeds. (a) The experimental setup for the fracture experiments. (b) Two sets of stress–strain curves resulting from compression tests. Seeds where compressed when dry or after
![]() $48$
hour humidification. (c) The stiffness was obtained by fitting the initial slopes of the curves. (d) The resulting stiffness is reported for dry and hydrated seeds. A statistical test (t-test) indicates that differences between the two groups are significant (
$48$
hour humidification. (c) The stiffness was obtained by fitting the initial slopes of the curves. (d) The resulting stiffness is reported for dry and hydrated seeds. A statistical test (t-test) indicates that differences between the two groups are significant (
![]() $p<0.05$
). (e,f) Two scanning electron micrographs of fractured seeds.
$p<0.05$
). (e,f) Two scanning electron micrographs of fractured seeds.
In order to better understand the role of puzzle-shaped cell in the mechanics of tobacco seeds, we resorted to numerical simulations. As discussed in the ‘Materials and methods’ section, we created a cellular structure mimicking the morphology of tobacco seed coats (see Figure 5a). As a reference, we compared this structure with a similar structure where cell walls are straight instead of undulated (see Figure 5d). We then used the finite element method, using COMSOL multiphysics, to investigate the deformation of these two structures under uniaxial stretching. Figure 5a,b and d,e displays the Von Mises stresses recorded in the wavy-edge and straight-edge cell structures, respectively (see also Supplementary Movies S5 and S6). The stress–strain curves reported in Figure 5c for the two structures showed that puzzle-shaped cell structures can achieve larger deformations with lower stresses. By analysing the lateral deformation of the structures as a function of the longitudinal one (see Figure 5f), we also showed that the puzzle-shaped cell structure displays a lower Poisson’s ratio (
![]() $\nu =0.97$
for the puzzle-shaped cell structure compared with
$\nu =0.97$
for the puzzle-shaped cell structure compared with
![]() $\nu =1.08$
for the straight-edge structure). Notice that the fact that Poisson’s ratios are larger than 0.5 is due to non-isotropic architectured nature of the structures we considered.
$\nu =1.08$
for the straight-edge structure). Notice that the fact that Poisson’s ratios are larger than 0.5 is due to non-isotropic architectured nature of the structures we considered.
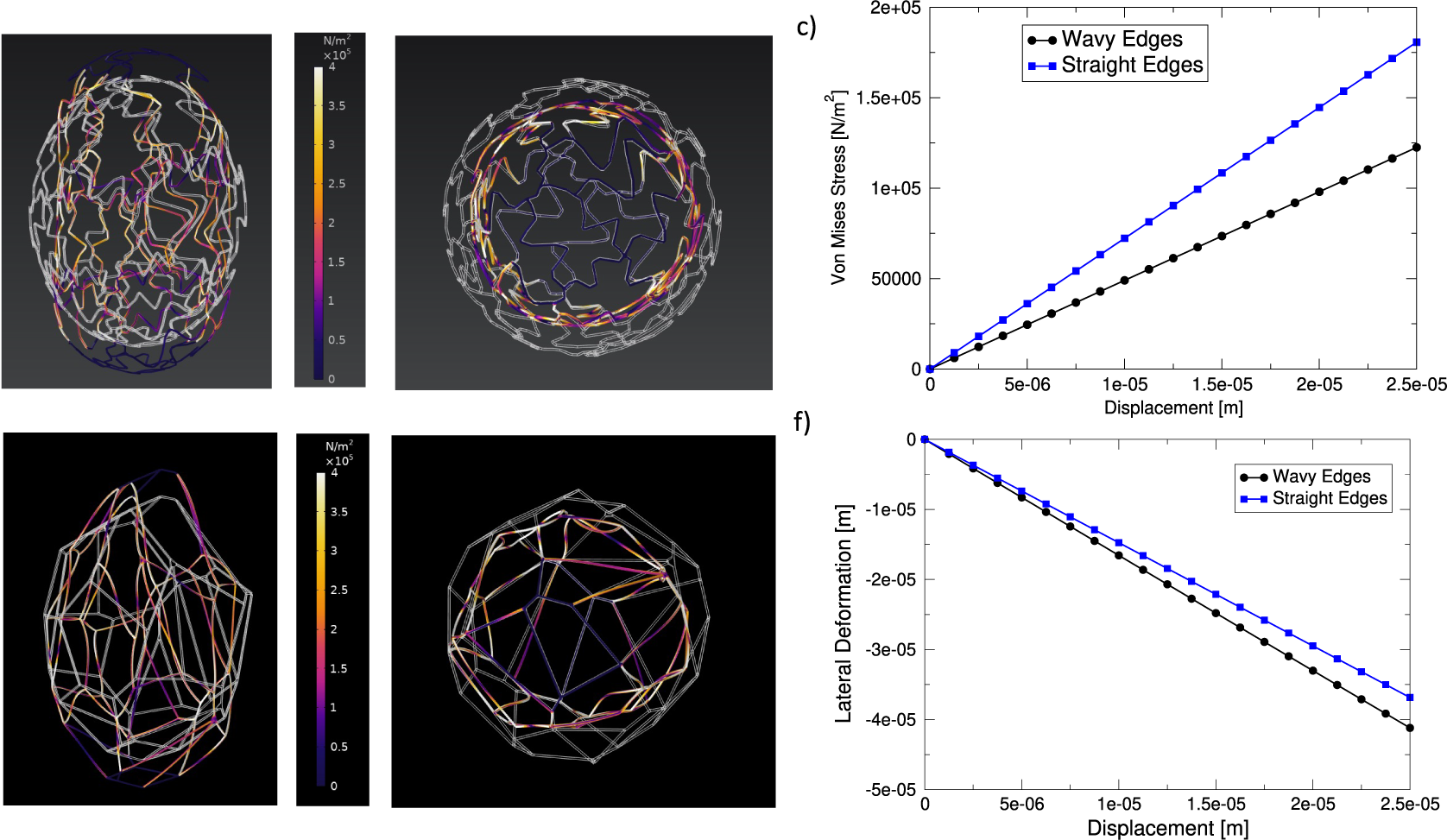
Figure 5. Deformation of seed-inspired structures. (a,b) Structure with wavy edges, representing puzzle-shaped cells. The undeformed structure is depicted in white and overlaid to the deformed structure which is coloured according to the value if the local Von Mises stress. Panel (a) shows the axial view and panel (b) the transverse section. (c) Stress versus axial displacement curve for the structures. (d,e) The same as (a,b) but for a structure with straight edges. (f) Lateral displacement as a function of axial displacement for the two structures.
Discussion
The coat of tobacco seeds display puzzle-shaped cells, also known as jigsaw puzzle cells or interlocking cells, a fascinating feature found in certain plant tissues and seeds (Thompson, Reference Thompson1942). These specialised cells have unique shapes and fit together like puzzle pieces, creating a tight and seamless connection between adjacent cells. In plant tissues, puzzle-shaped cells are commonly found in the epidermis, which is the outermost layer of cells covering leaves, stems, and other plant organs. The puzzle-like pattern of these cells contributes to the epidermis’ function as a protective barrier against environmental stresses such as water loss, pathogens, and mechanical damage (Jacques et al., Reference Jacques, Verbelen and Vissenberg2014). The interlocking nature of these cells helps enhance the structural integrity and strength of the epidermis, making it more resistant to external forces (Sapala et al., Reference Sapala, Runions and Smith2019).
In addition to their protective function, puzzle-shaped cells are also found to participate in regulating gas exchange (Glover, Reference Glover2000) and optimizing light capture (Galletti and Ingram, Reference Galletti and Ingram2015). The intricate cell boundaries create small gaps, known as stomata, which are essential for the exchange of gases, such as oxygen and carbon dioxide, between the plant and its surroundings. Stomata are most commonly found on leaves and allow for efficient gas diffusion, crucial for photosynthesis and respiration. Puzzle-shaped cells are not limited to plant tissues; they can also be found in seeds. For instance, in N. tabacum seed coats, the outer protective layer surrounding the embryonic plant, cells are intricately interlocked to form a tight seal. This seal helps prevent water loss and protects the developing embryo from desiccation, pathogens, and mechanical damage.
The formation of puzzle-shaped cells is a result of intricate cell wall development and patterning (Sapala et al., Reference Sapala, Runions, Routier-Kierzkowska, Gupta, Hong, Hofhuis, Verger, Mosca, Li, Hay, Hamant, AHK, Tsiantis, Prusinkiewicz and Smith2018). The study of puzzle-shaped cells in plants and seeds has attracted significant attention in plant biology and bioengineering. Understanding the molecular mechanisms and genetic regulation behind the formation of these cells can provide insights into plant development, tissue engineering, and crop improvement. Researchers have investigated the genetic factors that control cell shape, the role of signaling molecules, the impact of environmental factors, and of mechanical forces on puzzle-shaped cell formation (Sapala et al., Reference Sapala, Runions and Smith2019).
In this paper, we presented a combination of experimental observations and numerical simulations to elucidate the mechanical and geometrical aspects of tobacco seed coat rupture. Our results confirm that the effect of hydration is to make the seed coat softer and weaker, thus facilitating the germination process. The puzzle-shaped cell structure of the tobacco seed coat has the effect to reduce internal stresses on the coat which could be advantageous for the seed to be able to sustain large deformations as also discussed for other plant cells (Hasseldine et al., Reference Hasseldine, Gao, Collins, Jung, Jang, Song and Li2017; Sapala et al., Reference Sapala, Runions, Routier-Kierzkowska, Gupta, Hong, Hofhuis, Verger, Mosca, Li, Hay, Hamant, AHK, Tsiantis, Prusinkiewicz and Smith2018).
There are a number of important issues that have to be discussed for a proper interpretation of the experimental results presented in the present paper: We have mainly discussed the mechanical properties of the seed coat, but there could be also a mechanical contribution due to the internal tissues, the embryo, and the endosperm. Experimental results suggest hydration also weakens the endosperm facilitating germination (Manz et al., Reference Manz, Muller, Kucera, Volke and Leubner-Metzger2005). While the mechanical properties are dependent on the internal structure of the seed, we focused on the mechanical effect of the presence of puzzle shape cells which should not depend on the internal structure. In this paper, we also compared the behaviour of the seed under experimental compression to the behaviour during germination. From a mechanical point of view, however, these processes are different, since during germination localised tensile load is applied from the inside, whereas in compression deformation is applied from the outside. The seed coat is stiff and resistant to compressive load applied from the outside, but could more easily be pierced from the inside by the germinating radicle. We thus conclude that the most likely mechanical function of puzzle-shaped cells in N. tabacum seed coats is to provide enhanced protection against rupture before germination is completed.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/pma.2024.1.
Data availability statement
Data are available upon request.
Acknowledgements
We thank M. R. Fumagalli and M. C. Lionetti for useful discussions and R. Zulkarnain for help in the preparation of Figure 4. We are also grateful to A. Moscatelli and E. Onelli for providing the tobacco seeds and to V. Parravicini for his contribution to the cultivation of the plants.
Funding statement
SB was partially supported by the European Union Horizon 2020 research and innovation program under Grant Agreement No. 857470 and from the European Regional Development Fund under the program of the Foundation for Polish Science International Research Agenda PLUS, grant No. MAB PLUS/2018/8.
Competing interest
The authors declare that they have no known competing financial interests.
Author contributions
S.B. performed finite element calculations. M.B., C.F., S.M., C.A.B., and A.T. performed experiments. O.C. and S.Z. analysed data. C.A.M.L.P. and S.Z. designed and coordinated the study and wrote the paper.










