Published online by Cambridge University Press: 15 September 2014
§1. Einstein has shown that the gμv giving the metric, ds2 = gμvdxμdxv, for a unified field theory can be expressed in terms of the two tensors ahμahv by
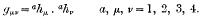
page 327 note * Preussischen Akademie der Wissenschaften Phy.-Math. Klasse, 1928, “Neue Möglichkeit für eine einheitliche Feldtheorie,” and Ibid., 1929, “Zur einheitliche Feldtheorie.”
page 327 note † Ibid., 1930, “Zwei strenge statische Lösungen der Feldgleichungen,” equations (53).
page 327 note ‡ Ibid., equations (50), (37), (44). As a matter of fact, in (44) μ is defined as
but, as will be shown later, the sign of m must be changed so that the metric obtained when e is zero shall represent an attractive force.
page 328 note * In the General Theory of Relativity, Einstein obtained θ′u 2 = k; e.g. The Mathematical Theory of Relativity, by A. S. Eddington (C.U.P.), second edition, p. 86, equation (39·41). Equation (5) reduces to this when e = 0.
page 329 note * Equation (11) is the justification for changing the sign of m in the definition of μ (see note on p. 327); otherwise (11) would have represented a repulsive force.
page 330 note * The Mathematical Theory of Relativity, p. 88, equation (40.6).
page 330 note † Ibid., p. 91, § 41.
page 330 note ‡ Ibid., p. 91, § 42.