Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-24T09:04:32.776Z Has data issue: false hasContentIssue false
  • English
  • Français

XII.—Matrices and Continued Fractions

Published online by Cambridge University Press:  15 September 2014

H. W. Turnbull
Get access

Extract

In a communication to this Society in 1916 Professor E. T. Whittaker gave an illuminating exposition of the use of matrices in dealing with continued fractions. In particular he discussed the problem of differentiating the following function of x:—

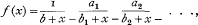
the value of f′(x) being obtained in the first instance from the leading element in the square of a certain reciprocal matrix {M(x)}−1 (cf. formula (9), § 3, below) by a method which I have recapitulated at the opening of § 4. The expression for f′(x) was then given as the quotient of two determinants obtained in a simple and specific manner from the matrix M(x) itself. It was remarked that this treatment of continued fractions takes its rise in a work by Sylvester, who incidentally showed that the fraction f(x) could be expressed as the quotient of two determinants. It was clear that this quotient expressed the leading element in the reciprocal of the matrix M(x): and the question naturally arose, what were the values of the other elements of this reciprocal?

Type
Proceedings
Information
Proceedings of the Royal Society of Edinburgh , Volume 53 , 1934 , pp. 151 - 163
Copyright
Copyright © Royal Society of Edinburgh 1934

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

1.Sylvester, , 1853. Phil. Mag., (4), vol. v, p. 446, and vol. vi, p. 297. Collected Works, vol. i, pp. 609, 641.CrossRefGoogle Scholar
2.Whittaker, E. T., 1916. Proc. Roy. Soc. Edin., vol. xxxvi, pp. 243–255.Google Scholar
3.Smith, H. J. S., 1861. Phil. Trans., vol. cli, pp. 293–326. Collected Works, vol. i, pp. 367–406.Google Scholar
4.Turnbull, and Aitken, , 1932 (Glasgow). Canonical Matrices, p. 106; p. 62.Google Scholar
5.Perron, , 1913 (Teubner). Die Lehre von dem Kettenbrüchen, p. 254.Google Scholar
Pringsheim, , 1898. Münchener Sitzungsberichte, vol. xxviii.Google Scholar
6.Jacobi, , 1868. Journal für reine und angew Math…. vol. lxix, pp. 29–64.Google Scholar
Perron, , 1907. Math. Annalen, vol. lxiv, p. 1.CrossRefGoogle Scholar
Maunsell, , 1929. Proc. Lond. Math. Soc., (2), vol. xxx, p. 127.Google Scholar
Paley, and Ursell, , 1929. Proc. Cambridge Phil. Soc., vol. xxvi, pp. 127—144.Google Scholar
Milne-Thomson, , 1933. Proc. Edin. Math. Soc., (2), vol. iii.Google Scholar