Published online by Cambridge University Press: 15 September 2014
§ 1. Object of Paper.—The chief object of the present paper is to establish the following theorem:
The functions of Lamé [that is to say, the doubly-periodic solutions of the differential equation
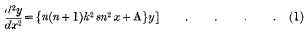
are the solutions of the homogeneous integral-equation
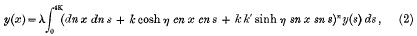
where η denotes an arbitrary constant.
page 71 note * Lamé's differential equation (1) when expressed in algebraic form has four regular singularities. Mathieu's differential equation
when expressed in algebraic form has two regular singularities and one irregular singularity, which latter may be regarded as formed by the confluence of two other regular singularities, making four in all. Legendre's differential equation has three regular singularities: and Bessel's equation is a confluent form of Legendre's.