VIII.—On the Theory of Graduation

Extract

The mathematical theory of graduation or adjustment, which hitherto has been developed chiefly in connection with the needs of actuarial science, centres round the following problem: A set of numbers u₁, u₂, u₃, … u_n is supposed to have been obtained from observations or statistics of some kind. These numbers would represent the values of a variable u_x corresponding to the values 1, 2, … n of its argument x, were it not that they are affected by accidental irregularities due to errors of observation, or to the imperfections of statistics. It is desired to construct a set of numbers 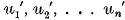, which represent the most probable true values of the variable u_x corresponding to these values of x, so that the “graduated” numbers 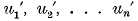differ as little as possible from the “ungraduated” numbers u₁, u₂, … u_n, but are freed from the accidental irregularities, and thus form a “smooth” sequence, i.e. a sequence from which a regular difference-table can be formed for use in various calculations.