Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-27T17:38:19.631Z Has data issue: false hasContentIssue false
  • English
  • Français

IX.—A Reduction-formula for the Functions of the Second Kind connected with the Polynomials of Applied Mathematics

Published online by Cambridge University Press:  15 September 2014

Pierre Humbert
Get access

Extract

In the course of an investigation regarding rotating fluids, I have had occasion to make considerable use of Legendre's function of the second kind, which, as is well known, may be expressed in the form

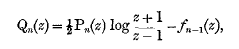
where Pn is Legendre's polynomial, and fn−1 a polynomial of degree n−1. Various expressions of fn−1 have been given, particularly in terms of Legendre's polynomials of lower degrees; but I found that none was satisfactory in regard to the practical computations which I had to perform.

Type
Proceedings
Information
Proceedings of the Royal Society of Edinburgh , Volume 38 , 1919 , pp. 61 - 69
Copyright
Copyright © Royal Society of Edinburgh 1919

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 61 note * Comptes Rendus, t. 165, p. 759.

page 61 note † Comptes Rendus, p. 699.

page 65 note * For the properties, expansions, recurrence-formulæ, etc., of the function Cnν, the reader is referred to Whittaker and Watson, Modern Analysis, p. 323. See also Appell and Lambert, Généralisations des fonctions sphériques (Edition Française de l'Encyclopédie, ii, 5), p. 237.

page 67 note * Laguerre, Œuvres, 1, p. 428. Appell and Lambert, op. cit., p. 236. These polynomials can be expressed in terms of the confluent hypergeometric function Wk, m.

page 68 note * Whittaker, Proc. Lond. Math. Soc., xxxv; Arch. Milne, Proc. Edin. Math. Soc., xxxii.