Article contents
On the General Scalar Function of a Vector
Published online by Cambridge University Press: 15 September 2014
Extract
The general scalar function of a vector ρ may evidently be written in the form
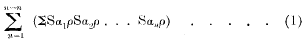
where α1 … αn are constant vectors, each term being homogeneous in ρ. If the factors of each term of any one of the brackets be permuted in every possible way, i.e., in |r ways (where r is the degree of the set of terms chosen), it can be written in the form

where φρr−1 is a vector function of ρ of the (r − l)th degree, the index (r − 1) serving merely to indicate the degree of the function. This notation will be found to lead to no confusion, and to have great advantages. Since the variable ρ occurs in φ along with each vector α, and also these vectors have been arranged in every possible way, it follows that, if in each term of φ we replace s of the ρ's by any other vector σ in such a way that the order of occurrence of the ρ's and the σ's is the same in each term, then the final result is independent of that order; that is to say,
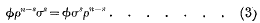
- Type
- Proceedings
- Information
- Copyright
- Copyright © Royal Society of Edinburgh 1904
- 1
- Cited by


