No CrossRef data available.
Article contents
II.—On the Equations of Motion of a Single Particle
Published online by Cambridge University Press: 15 September 2014
Extract
§ 1. When solved for the second derivatives, the Lagrangian equations of motion for a system in which there are no extraneous forces have the form
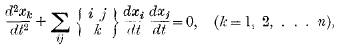
or, disregarding the parameter t,
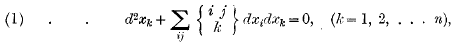
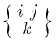 being the second Christoffel symbol † of the matrix associated with the kinetic energy. If there are extraneous forces Fk and, denoting t by xn+1, we add
being the second Christoffel symbol † of the matrix associated with the kinetic energy. If there are extraneous forces Fk and, denoting t by xn+1, we add 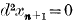 to the set of equations, the equations of motion are
to the set of equations, the equations of motion are
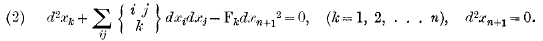
- Type
- Proceedings
- Information
- Copyright
- Copyright © Royal Society of Edinburgh 1922
References
page 26 note * Cf. Whittaker, Analytical Dynamics, p. 39; or Wright, Invariants of Quadratic Differential Forms, p. 83.
page 26 note † The definition and properties of these symbols may be found in Wright, loc. cit., p. 10.
page 26 note ‡ If there is more than one particle in question, it may be necessary to introduce more than one time variable. In many ways it is best to consider these as strictly space variables and to assume that particles in our universe are moving in the direction of the fourth space direction so nearly uniformly in straight lines that the distances measured in this direction are, to a first approximation, proportional to the time.
page 28 note * This seems the most natural way of introducing the form (11) into the dynamical system. It suggests that it is natural to consider this form as defining time rather than distance, thus leaving open the possibility of using a different form to define the geometry of space.
page 30 note * Cf. Wright, loc. cit., p. 53.
page 30 note † The Einstein value is obtained by setting
page 31 note * Cf. Levi-Civita, , “Statica Einsteiniana,” Rom. Acc. L. Rend., xxvi (1917), p. 458Google Scholar, where the connection with Einstein's equations is discussed.
page 31 note † There are, of course, other cases in which an explicit solution of (21) can be obtained, e.g. when 2V + A is a function of A and x4 alone, or if A has the form A1(V) + x 4A2(V).
page 33 note * Kottler, F., Ann. d. Phys., lvi (1918), p. 401.CrossRefGoogle Scholar


