No CrossRef data available.
Published online by Cambridge University Press: 15 September 2014
Now it is at once manifest that the successive developments here obtained of the determinant [xyzt] are letter by letter identical with the successive “lignes” obtained by Bézout from the unreal product xyzt; but that instead of having one arbitrary step succeeding another, as in the application of Bezout's rule, there is here a fluent reasonableness characterising the whole process.* As for the peculiarities requiring elucidation in the series of special examples above referred to, they are seen, when looked at in this light, to be but matters of course.
* If the fact at the basis of the process were made use of nowadays, it would be advantageous, of course, in the first instance to simplify the determinant as much as possible. For example, the equations being (Bezout, p. 178)
note * page 456 * Should be n.
note * page 458 It is very curious to observe, in passing, that although Bezout does not obtain all his vanishing aggregates directly by means of the principle which he ao carefully states at the commencement, nevertheless every one of them can be so obtained. He does not extend the principle beyond the case where only one of the original equations is repeated. If, however, we take the equations ![]()
![]() repeat both of them so as to have a set of four, and then proceed by the méthode pour abréger to find the iquatwn de condition, we obtain
repeat both of them so as to have a set of four, and then proceed by the méthode pour abréger to find the iquatwn de condition, we obtain 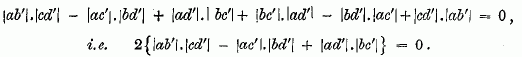 . This is the identity at foot of p. 457, and all the others are readily seen to be obtainable in the same way.
. This is the identity at foot of p. 457, and all the others are readily seen to be obtainable in the same way.
* My best thanks are due the Committee of Management of Uniyersity College, London, for the loan of a copy of Hindenburg's tract from the Graves Library.
note * page 467 Lagrange's use of a corresponding letter from a different alphabet must not be forgotten.
note * page 475 An abstract of this is given in the Nouv. Bull, des Sciences par la Société Philomatique, ii. pp. 312–316.
* It will be seen that the order in which the permutations come to hand in this process of tabulation is the order in which they would be arranged according to magnitude if each permutation were viewed as a number of which α, β, γ, δ were the digits, α being < β < γ < δ (“ordo lexicographicus,” “lexicographische Anordnung” of Hindenburg).
note * page 486 There is an extension here which one is scarcely prepared for, viz., “le produit d'un nombre quelconque de sommes de produits,” instead of la somme dun nombre de produits.
note * page 487 Meant for Σad.
note * page 510 Misprint in original, for Dn-1.