A sequence of non-negative random variables {Xi} is called a renewal process, and if the Xi may only take values on some sequence 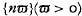 it is termed a discrete renewal process. The greatest k such that X1 + X2 + … + Xk ≤ x(> o) is a random variable N(x) and theorems concerning N(x) are renewal theorems. This paper is concerned with the proofs of a number of renewal theorems, the main emphasis being on processes which are not discrete. It is assumed throughout that the {Xi} are independent and identically distributed.
it is termed a discrete renewal process. The greatest k such that X1 + X2 + … + Xk ≤ x(> o) is a random variable N(x) and theorems concerning N(x) are renewal theorems. This paper is concerned with the proofs of a number of renewal theorems, the main emphasis being on processes which are not discrete. It is assumed throughout that the {Xi} are independent and identically distributed.
If H(x) = Ɛ{N(x)} and K(x) is the distribution function of any non-negative random variable with mean K > o, then it is shown that for the non-discrete process
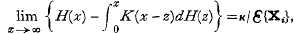
where Ɛ{Xi} need not be finite; a similar result is proved for the discrete process. This general renewal theorem leads to a number of new results concerning the non-discrete process, including a discussion of the stationary “age-distribution” of “renewals” and a discussion of the variance of N(x). Lastly, conditions are established under which
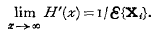
These new conditions are much weaker than those of previous theorems by Feller, Täcklind, and Cox and Smith.