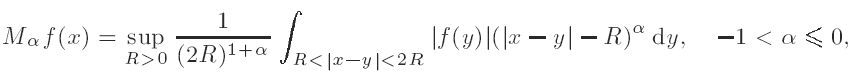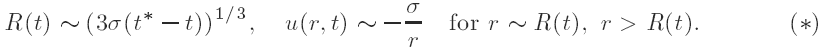Research Article
Co-actions of groups
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 225-239
-
- Article
- Export citation
Structure of the Fučík spectrum and existence of solutions for equations with asymmetric nonlinearities
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 241-265
-
- Article
- Export citation
Weighted inequalities for a maximal function on the real line
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 267-277
-
- Article
- Export citation
Relaxation of some multi-well problems
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 279-320
-
- Article
- Export citation
Qualitative behaviour of positive solutions of a predator—prey model: effects of saturation
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 321-349
-
- Article
- Export citation
Duality relations for nonlinear incompressible two-dimensional elasticity
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 351-369
-
- Article
- Export citation
A note on the dissolution of spherical crystals
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 371-389
-
- Article
- Export citation
Analyticity of solitary wave solutions to generalized Kadomtsev—Petviashvili equations
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 391-424
-
- Article
- Export citation
Infiltrations in immiscible fluids systems
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 425-436
-
- Article
- Export citation
Global solution to the equations of viscous gas flows
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 437-449
-
- Article
- Export citation
A general blow-up result on nonlinear boundary-value problems on exterior domains
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 451-475
-
- Article
- Export citation
Corrigendum
Corrigendum
-
- Published online by Cambridge University Press:
- 11 July 2007, p. 477
-
- Article
-
- You have access
- Export citation