Research Article
On the Benney equation
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 1121-1144
-
- Article
- Export citation
Sharp upper bounds for the density of some invariant measures
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 1145-1161
-
- Article
- Export citation
Multiple positive solutions for a critical elliptic system with concave—convex nonlinearities
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 1163-1177
-
- Article
- Export citation
Travelling wavefronts for a non-divergent degenerate and singular parabolic equation with changing sign sources
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 1179-1207
-
- Article
- Export citation
Well-posedness of some initial—boundary-value problems for dynamo-generated poloidal magnetic fields
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 1209-1235
-
- Article
- Export citation
Two-dimensional incompressible viscous flow around a thin obstacle tending to a curve
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 1237-1254
-
- Article
- Export citation
Evaluating norms of Pettis integrable functions
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 1255-1259
-
- Article
- Export citation
The inverse nodal problem and the Ambarzumyan problem for the p-Laplacian
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 1261-1273
-
- Article
- Export citation
Decompositions of groups of invertible elements in a ring
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 1275-1287
-
- Article
- Export citation
Bounds for blow-up time for the heat equation under nonlinear boundary conditions
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 1289-1296
-
- Article
- Export citation
Multiple positive solutions for an unbounded Dirichlet boundary problem involving sign-changing weight
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 1297-1325
-
- Article
- Export citation
Pseudo-immersions of oriented surfaces with one boundary component into the plane
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 1327-1335
-
- Article
- Export citation


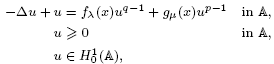
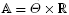 is an infinite strip in ℝ
is an infinite strip in ℝ