Research Article
Minimizers for a double-well problem with affine boundary conditions
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 439-466
-
- Article
- Export citation
On compactness results for multi-scale convergence
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 467-476
-
- Article
- Export citation
Fourier splitting and dissipation of nonlinear dispersive waves
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 477-502
-
- Article
- Export citation
Travelling-waves for the FKPP equation via probabilistic arguments
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 503-517
-
- Article
- Export citation
Heteroclinic orbits between rotating waves in hyperbolic balance laws
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 519-538
-
- Article
- Export citation
A study of Jacobians in Hardyd–Orlicz spaces
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 539-570
-
- Article
- Export citation
Linear stability analysis and metastable solutions for a phase-field model
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 571-600
-
- Article
- Export citation
Some geometric properties of the set of generalized Young functionals
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 601-616
-
- Article
- Export citation
On the motion of a vortex filament in an external flow according to the localized induction approximation
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 617-626
-
- Article
- Export citation
Existence of the solutions for the Ginzburg–Landau equations of superconductivity in three spatial dimensions
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 627-639
-
- Article
- Export citation
The finite basis problem for the semigroups of order-preserving mappings
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 641-647
-
- Article
- Export citation
Liouville theorems on some indefinite equations
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 649-661
-
- Article
- Export citation
Front matter
PRM volume 129 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PRM volume 129 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
-
- Article
-
- You have access
- Export citation

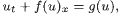
 for this equation with
for this equation with