Article contents
Zero-electron-mass limit of the compressible Navier–Stokes–Poisson equations with well/ill-prepared initial data
Published online by Cambridge University Press: 01 August 2022
Abstract
In this study, we consider the viscous compressible Navier–Stokes–Poisson equations, which consist of the balance laws for electron density and moment, and a Poisson equation for the electrostatic potential. The limit of vanishing electron mass of this system with both well/ill-prepared initial data on the whole space is rigorously justified within the framework of local smooth solution. We first make use of the symmetric hyperbolic–parabolic structure of the compressible Navier–Stokes–Poisson equation to obtain uniform estimate in the short time, by which we show uniform existence of local classical solution to the compressible Navier–Stokes–Poisson equation in $\mathbb {R}^d(d\geq 1)$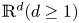 . Further, with uniform estimate of time derivatives, we show the zero-electron-mass limit of the solutions for the compressible Navier–Stokes–Poisson equation with well-prepared initial data in $\mathbb {R}^d(d\geq 1)$
. Further, with uniform estimate of time derivatives, we show the zero-electron-mass limit of the solutions for the compressible Navier–Stokes–Poisson equation with well-prepared initial data in $\mathbb {R}^d(d\geq 1)$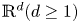 by using Aubin's lemma. A detailed spectral analysis on the linearized system is done so that we are able to prove the zero-electron-mass limit of the solutions with ill-prepared initial data in $\mathbb {R}^d(d\geq 3)$
by using Aubin's lemma. A detailed spectral analysis on the linearized system is done so that we are able to prove the zero-electron-mass limit of the solutions with ill-prepared initial data in $\mathbb {R}^d(d\geq 3)$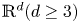 , where the convergence occurs away from the time $t=0$
, where the convergence occurs away from the time $t=0$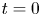 . Finally, note that the dissipation mechanism for the linearized compressible Navier–Stokes–Poisson system is different from that of the compressible Euler equations in Grenier (Commun. Partial Diff. Eqns. 21 (1996), 363–394); Grenier (Commun. Pure Appl. Math. 50 (1997), 821–865); Ukai (J. Math. Kyoto Univ. 26 (1986), 323–331), or that of the compressible Euler–Poisson equations in Ali and Chen (Nonlinearity 24 (2011), 2745–2761), since its eigenvalues are somehow similar to that of heat equation, and the fundamental solution contains a part behaving like the heat kernel, thus a big difficulty is the singularity of the heat kernel at $t=0$
. Finally, note that the dissipation mechanism for the linearized compressible Navier–Stokes–Poisson system is different from that of the compressible Euler equations in Grenier (Commun. Partial Diff. Eqns. 21 (1996), 363–394); Grenier (Commun. Pure Appl. Math. 50 (1997), 821–865); Ukai (J. Math. Kyoto Univ. 26 (1986), 323–331), or that of the compressible Euler–Poisson equations in Ali and Chen (Nonlinearity 24 (2011), 2745–2761), since its eigenvalues are somehow similar to that of heat equation, and the fundamental solution contains a part behaving like the heat kernel, thus a big difficulty is the singularity of the heat kernel at $t=0$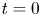 .
.
Keywords
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 5 , October 2023 , pp. 1439 - 1466
- Copyright
- Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
- 1
- Cited by



