Article contents
XXIII.—On an Extension to an Integro-differential Inequality of Hardy, Littlewood and Polya*
Published online by Cambridge University Press: 14 February 2012
Synopsis
This paper considers an extension of the following inequality given in the book Inequalities by Hardy, Littlewood and Polya; let f be real-valued, twice differentiable on [0, ∞) and such that f and f are both in the space fn, ∞), then f′ is in L,2(0, ∞) and

The extension consists in replacing f′ by M[f] where
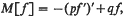
choosing f so that f and M[f] are in L2(0, ∞) and then seeking to determine if there is an inequality of the form

where K is a positive number independent of f.
The analysis involves a fourth-order differential equation and the second-order equation associated with M.
A number of examples are discussed to illustrate the theorems obtained and to show that the extended inequality (*) may or may not hold.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 69 , Issue 4 , 1972 , pp. 295 - 333
- Copyright
- Copyright © Royal Society of Edinburgh 1972
References
References to Literature
- 5
- Cited by


