No CrossRef data available.
Article contents
X.—The Two Parameter Sturm-Liouville Problem for Ordinary Differential Equations*
Published online by Cambridge University Press: 14 February 2012
Synopsis
This paper discusses the existence, under fairly general conditions, of solutions of the two-parameter eigenvalue problem denned by the differential equation,
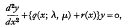
and three point Sturm-Liouville boundary conditions.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 69 , Issue 2 , 1971 , pp. 139 - 148
- Copyright
- Copyright © Royal Society of Edinburgh 1971


