Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T19:01:09.243Z Has data issue: false hasContentIssue false
  • English
  • Français

XIII.—The Generating Function of Solid Partitions

Published online by Cambridge University Press:  14 February 2012

E. M. Wright
E. M. Wright
Affiliation:
University of Aberdeen.
Get access Rights & Permissions [Opens in a new window]

Synopsis

The generating function for the number of linear partitions was found by Euler, the method being almost trivial. That for plane partitions is due to Macmahon, but, even in a simplified form found by Chaundy, the proof is far from trivial. The number of solid partitions of n, i.e. the number of solutions of

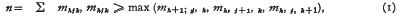
is denoted by r(n). It has often been conjectured that the generating function of r(n) is 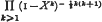, but this is now known to be false. We write η(a, b, c) for the generating function of the number of solutions of (1) subject to the additional condition that

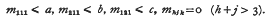
Macmahon 1916 found n(a, 1, 1) for general a. Here we find η(a, b, c) for general a, b. c.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 67 , Issue 3 , 1967 , pp. 185 - 195
Copyright
Copyright © Royal Society of Edinburgh 1967

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

Chaundy, T. W., 1931. “Partition-generating Functions”, Quart. J. Math., 2, 234–240.CrossRefGoogle Scholar
Euler, L., 1747. Introductie' in analysin infinitorum 1 Lausanne;, cap. 16; Opera omnia (I) (Leipzig 1922), VIII, 313–338.Google Scholar
Macmahon, P. A., 1916. Combinatory Analysis, vol. 2 (Cambridge).Google Scholar