No CrossRef data available.
Article contents
X.—Determinants for Matrices over Lattices
Published online by Cambridge University Press: 14 February 2012
Extract
In the literature concerning matrices whose co-ordinates are elements of a Boolean lattice, one may find three different definitions for the determinant of a matrix. We shall call these the first, second and third determinant and will denote the value of the ith determinant of a matrix A by |A |i for i = 1, 2, 3. The first determinant may be defined for square matrices over an arbitrary lattice. The second and third determinants may be defined for square matrices over any lattice L with a greatest element I, a least element o and an orthocomplementation′: L→L, that is a′ is a complement of a, a = a″ and a ≤ b implies that b′ ≤ a′ for all a, b in L. In this paper we obtain some elementary properties of these determinants in this general setting and in the particular case where L is an orthomodular lattice, that is a lattice with o, 1 and an orthocomplementation' such that
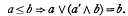
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 68 , Issue 2 , 1969 , pp. 138 - 144
- Copyright
- Copyright © Royal Society of Edinburgh 1969


