Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T08:47:47.115Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted Lorentz norm inequalities for general maximal operators associated with certain families of Borel measures

Published online by Cambridge University Press:  14 November 2011

María Dolores Sarrión Gavilán
María Dolores Sarrión Gavilán
Affiliation:
Departamento de Economía Aplicada (Estadística y Econometría), Facultad de Ciencias Económicas y Empresariales, Universidad de Málaga, 29013 Málaga, Spain
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a certain family ℱ of positive Borel measures and γ ∈ [0, 1), we define a general onesided maximal operator 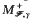and we study weighted inequalities in Lp,q spaces for these operators. Our results contain, as particular cases, the characterisation of weighted Lorentz norm inequalities for some well-known one-sided maximal operators such as the one-sided Hardy–Littlewood maximal operator associated with a general measure 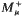, the one-sided fractional maximal operator 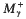and the maximal operator 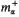associated with the Cesèro-α averages.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 128 , Issue 2 , 1998 , pp. 403 - 424
Copyright
Copyright © Royal Society of Edinburgh 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Andersen, K. F.. Weighted inequalities for maximal functions associated with general measures. Trans. Amer. Math. Soc. 326 (1991), 907–20.CrossRefGoogle Scholar
2Andersen, K. F. and Sawyer, E. T.. Weighted norm inequalities for the Riemann-Liouville and Weyl fractional integral operators. Trans. Amer. Math. Soc. 308 (1988), 547–57.CrossRefGoogle Scholar
3Bernal, A.. A note on the one-dimensional maximal function. Proc. Roy. Soc. Edinburgh Sect. A 111 (1989), 325–28.CrossRefGoogle Scholar
4Broise, M., Déniel, Y. and Derriennic, Y.. Réarrangement, inégalités maximales et Théorémes ergodiques fractionnaires. Ann. Inst. Fourier, Grenoble 39 (1989), 689–714.Google Scholar
5Carbery, A., Hernández, E. and Soria, F.. Estimates for the Kakeya maximal operator and radial functions in ℝn (ICM-90 Proc. Satellite Conf. Harmonic Analysis, Sendai).Google Scholar
6Carbery, A., Romera, E. and Soria, F.. Radial weights and mixed norm inequalities for the disc multiplier (Preprint).Google Scholar
7Chung, H., Hunt, R. and Kurtz, D. S.. The Hardy-Littlewood maximal functions of L p,q spaces with weights. Indiana Univ. Math. J. 31 (1982), 109–20.Google Scholar
8Gurka, P. and Pick, L.. A∞ type condition for general measures. Real Anal. Exchange 17 (1992), 706–27.Google Scholar
9Hunt, R. A.. On L(p, q) spaces. Enseign. Math. 12 (1966), 249–76.Google Scholar
10Jurkat, W. and Troutman, J.. Maximal inqualities related to generalized a.e. continuity. Trans. Amer. Math. Soc. 252 (1979), 49–64.Google Scholar
11Kokilashvili, V. and Krbec, M.. Weighted inequalities in Lorentz and Orlicz spaces (Singapore: World Scientific, 1991).CrossRefGoogle Scholar
12Martin-Reyes, F. J.. Nonliner analysis, function spaces and applications 5 (Prague 1994) (Prague: Prometheus, 1994).Google Scholar
13Martín-Reyes, F.J., Salvador, P. Ortega and de la Torre, A.. Weighted inequalities for one-sided maximal functions. Trans. Amer. Math. Soc. 319 (1990), 517–34.CrossRefGoogle Scholar
14Martin-Reyes, F.J. and de la Torre, A.. Two weight norm inequalities for fractional one-sided maximal operators. Proc. Amer. Math. Soc. 117 (1993), 483–9.CrossRefGoogle Scholar
15Martin-Reyes, F. J. and de la Torre, A.. Some weighted inequalities for general one-sided maximal operators. Studia Math. 122 (1997), 1–14.Google Scholar
16Ortega, P.. Weighted Lorentz norm inequalities for the one-sided Hardy–Littlewood maximal functions and for the maximal ergodic operator. Canad. J. Math. 46 (1994), 1057–72.CrossRefGoogle Scholar
17Sawyer, E.. Weighted inequalities for the one sided Hardy-Littlewood maximal functions. Trans. Amer. Math. Soc. 297 (1986), 53–61.CrossRefGoogle Scholar
18Zygmund, A.. Trigonometric Series, vols I and II (Cambridge: Cambridge University Press, 1959).Google Scholar