Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T10:04:56.108Z Has data issue: false hasContentIssue false
  • English
  • Français

VI.—On Solvability of Some Two-Parameter Eigenvalue Problems in Hilbert Space

Published online by Cambridge University Press:  14 February 2012

Z. Bohte
Z. Bohte
Affiliation:
University of Surrey, London.
Get access Rights & Permissions [Opens in a new window]

Synopsis

This paper studies two particular cases of the general 2-parameter eigenvalue problem namely

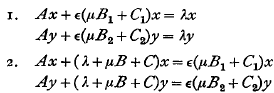
where A, B, B1, B2, C, C1, C2 are self-adjoint operators in Hilbert space, all except A being bounded. The disposable parameters λ and μ have to be determined so that the equations have non-trivial solutions x, y.

On the assumption that the solution is known for ∊ = o, solutions are constructed in the form of series for λ, μ, x, y as power series in ∊ with finite radius of convergence.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 68 , Issue 1 , 1968 , pp. 83 - 93
Copyright
Copyright © Royal Society of Edinburgh 1968

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

Arscott, F. M., 1964. “Two-parameter eigenvalue problems in differential equations”, Proc. Lond. Math. Soc., 14, 459–470.CrossRefGoogle Scholar
Atkinson, F. V., 1964. “Multivariate spectral theory”, MRC Tech. Summ. Rep., 431.Google Scholar
Hiller, F., and Schmidt, A., 1962. “Über ein Eigenwertproblem linearer Differentialoperatoren mit zwei Parametern”, Archs Ration. Mech. Analysis, 9, 439–444.CrossRefGoogle Scholar
Meixner, J., and Schäfke, F. W., 1954. Mathieusche Funktionen und Sphäroid-funktionen. Springer Verlag: Berlin.CrossRefGoogle Scholar