Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-12T12:44:11.692Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniform asymptotic expansions for oblate spheroidal functions I: positive separation parameter λ

Published online by Cambridge University Press:  14 November 2011

T. M. Dunster
T. M. Dunster
Affiliation:
Department of Mathematics, San Diego State University, San Diego, CA 92182-0314, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

Uniform asymptotic expansions are derived for solutions of the spheroidal wave equation, in the oblate case where the parameter µ is real and nonnegative, the separation parameter λ is real and positive, and γ is purely imaginary (γ = iu). As u →∞, three types of expansions are derived for oblate spheroidal functions, which involve elementary, Airy and Bessel functions. Let δ be an arbitrary small positive constant. The expansions are uniformly valid for λ/u2 fixed and lying in the interval (0,2), and for λ / u2when 0<λ/u2 < 1, and 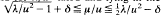when 1 = 1≦λ/u2 < 2. The union of the domains of validity of the various expansions cover the half- plane arg (z)≦ = π/2.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 121 , Issue 3-4 , 1992 , pp. 303 - 320
Copyright
Copyright © Royal Society of Edinburgh 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Arscott, F. M.. Periodic Differential Equations (Oxford: Pergamon Press, 1964).Google Scholar
2Boyd, W. G. C. and Dunster, T. M.. Uniform asymptotic solutions of a class of second-order linear differential equations having a turning point and regular singularity, with an application to Legendre functions. SIAM J. Math. Anal. 17 (1986), 422–450.CrossRefGoogle Scholar
3Dunster, T. M.. Uniform asymptotic expansions for prolate spheroidal functions with large parameters. SIAM J. Math. Anal. 17 (1986), 1495–1524.CrossRefGoogle Scholar
4Leitner, A. and Spence, R. D.. The oblate spheroidal wave functions. J. Franklin Inst. 249 (1950), 299–321.CrossRefGoogle Scholar
5Olver, F. W. J.. Asymptotics and Special Functions (New York: Academic Press, 1974).Google Scholar
6Paris, R. B. and Dagazian, R. Y.. The eigenvalues of the simplified ideal MHD ballooning equation. J. Math. Phys. 27(8) (1986), 2188–2202.CrossRefGoogle Scholar
7Sleeman, B. D.. Integral representations associated with high-frequency non-symmetric scattering by prolate spheroids. Quart. Appl. Math. 22 (1969), 405–426.CrossRefGoogle Scholar