Three-phase boundary motions under constant velocities. I: The vanishing surface tension limit

Abstract

In this paper, we deal with the dynamics of material interfaces such as solid–liquid, grain or antiphase boundaries. We concentrate on the situation in which these internal surfaces separate three regions in the material with different physical attributes (e.g. grain boundaries in a polycrystal). The basic two-dimensional model proposes that the motion of an interface Г_ij between regions i and j (i, j = 1, 2, 3, i ≠ j) is governed by the equation

Here V_ij, k_ij, μ_ij and f_ij denote, respectively, the normal velocity, the curvature, the mobility and the surface tension of the interface and the numbers F_ij stand for the (constant) difference in bulk energies. At the point where the three phases coexist, local equilibrium requires that

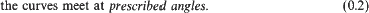
In case the material constants f_ij are small, 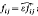and ε ≪ 1, previous analyses based on the parabolic nature of the equations (0.1) do not provide good qualitative information on the behaviour of solutions. In this case, it is more appropriate to consider the singular case with f_ij = 0. It turns out that this problem, (0.1) with f_ij = 0, admits infinitely many solutions. Here, we present results that strongly suggest that, in all cases, a unique solution—‘the vanishing surface tension (VST) solution’—is selected by letting ε→0. Indeed, a formal analysis of this limiting process motivates us to introduce the concept of weak viscosity solution for the problem with ε = 0. As we show, this weak solution is unique and is therefore expected to coincide with the VST solution. To support this statement, we present a perturbation analysis and a construction of self-similar solutions; a rigorous convergence result is established in the case of symmetric configurations. Finally, we use the weak formulation to write down a catalogue of solutions showing that, in several cases of physical relevance, the VST solution differs from results proposed previously.