Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Huang, Yisheng
Wu, Tsung-Fang
and
Wu, Yuanze
2015.
Multiple positive solutions for a class of concave–convex elliptic problems in ℝNinvolving sign-changing weight, II.
Communications in Contemporary Mathematics,
Vol. 17,
Issue. 05,
p.
1450045.
LIAO, Jiafeng
PU, Yang
and
TANG, Chunlei
2018.
Multiplicity of positive solutions for a class of concave-convex elliptic equations with critical growth.
Acta Mathematica Scientia,
Vol. 38,
Issue. 2,
p.
497.
Li, Hong-Ying
Pu, Yang
and
Liao, Jia-Feng
2020.
Multiple positive solutions for singular elliptic problems involving concave-convex nonlinearities and sign-changing potential.
Indian Journal of Pure and Applied Mathematics,
Vol. 51,
Issue. 2,
p.
611.
De Paiva, Francisco Odair
Lima, Sandra Machado de Souza
and
Miyagaki, Olimpio Hiroshi
2023.
Existence of at least four solutions for Schrodinger equations with magnetic potential involving and sign-changing weight function.
Electronic Journal of Differential Equations,
Vol. 2023,
Issue. 01-??,
p.
47.
de Paiva, Francisco Odair
de Souza Lima, Sandra Machado
and
Miyagaki, Olímpio Hiroshi
2024.
Nehari manifold for a Schrödinger equation with magnetic potential involving sign-changing weight function.
Applicable Analysis,
Vol. 103,
Issue. 6,
p.
1036.


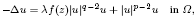
 . Assuming that
. Assuming that 