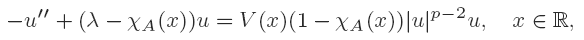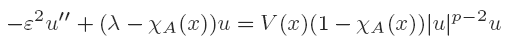Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Watanabe, Tatsuya
2005.
Existence of positive multi-peaked solutions to a nonlinear Schrödinger equation arising in nonlinear optics.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 62,
Issue. 5,
p.
925.
Watanabe, Tatsuya
2007.
On exterior Neumann problems with an asymptotically linear nonlinearity.
Journal of Differential Equations,
Vol. 240,
Issue. 1,
p.
1.