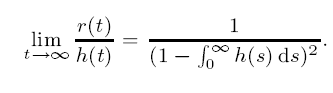Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Appleby, John
2002.
Almost Sure Stability of Linear Itô-Volterra Equations with Damped Stochastic Perturbations.
Electronic Communications in Probability,
Vol. 7,
Issue. none,
Appleby, John A.D.
and
Reynolds, David W.
2002.
On the Non-Exponential Convergence of Asymptotically Stable Solutions of Linear Scalar Volterra Integro-Differential Equations.
Journal of Integral Equations and Applications,
Vol. 14,
Issue. 2,
Appleby, John A.D.
and
Reynolds, David W.
2003.
Non-exponential stability of scalar stochastic Volterra equations.
Statistics & Probability Letters,
Vol. 62,
Issue. 4,
p.
335.
Appleby, John
and
Freeman, Alan
2003.
Exponential Asymptotic Stability of Linear Itô-Volterra Equation with Damped Stochastic Perturbations.
Electronic Journal of Probability,
Vol. 8,
Issue. none,
Appleby, John A.D.
and
Reynolds, David W.
2004.
On Necessary and Sufficient Conditions for Exponential Stability in Linear Volterra Integro-Differential Equations.
Journal of Integral Equations and Applications,
Vol. 16,
Issue. 3,
2005.
Volterra Integral and Differential Equations.
Vol. 202,
Issue. ,
p.
243.
2005.
Volterra Integral and Differential Equations.
Vol. 202,
Issue. ,
p.
340.
Applelby, John A. D.
Győri, István
and
Reynolds, David W.
2006.
On exact convergence rates for solutions of linear systems of Volterra difference equations†.
Journal of Difference Equations and Applications,
Vol. 12,
Issue. 12,
p.
1257.
Appleby, John A.D.
Győri, István
and
Reynolds, David W.
2006.
On exact rates of decay of solutions of linear systems of Volterra equations with delay.
Journal of Mathematical Analysis and Applications,
Vol. 320,
Issue. 1,
p.
56.
Győri, István
and
Horváth, László
2008.
New Limit Formulas for the Convolution of a Function with a Measure and Their Applications.
Journal of Inequalities and Applications,
Vol. 2008,
Issue. ,
p.
1.
Reynolds, David
and
Appleby, John
2008.
Decay Rates of Solutions of Linear Stochastic Volterra Equations.
Electronic Journal of Probability,
Vol. 13,
Issue. none,
Appleby, John A. D.
and
Buckwar, Evelyn
2010.
A Constructive Comparison Technique for Determining the Asymptotic Behaviour of Linear Functional Differential Equations with Unbounded Delay.
Differential Equations and Dynamical Systems,
Vol. 18,
Issue. 3,
p.
271.
Appleby, John A. D.
2010.
On Regularly Varying and History-Dependent Convergence Rates of Solutions of a Volterra Equation with Infinite Memory.
Advances in Difference Equations,
Vol. 2010,
Issue. ,
p.
1.
Appleby, John A.D.
and
Riedle, Markus
2010.
Stochastic Volterra equations in weighted spaces.
Journal of Integral Equations and Applications,
Vol. 22,
Issue. 1,
Zhao, Dianli
and
Han, Dong
2011.
Mean square exponential and non-exponential asymptotic stability of impulsive stochastic Volterra equations.
Journal of Inequalities and Applications,
Vol. 2011,
Issue. 1,
Appleby, John A.D.
and
Krol, Katja
2011.
Long memory in a linear stochastic Volterra differential equation.
Journal of Mathematical Analysis and Applications,
Vol. 380,
Issue. 2,
p.
814.
Appleby, John A.D.
and
Daniels, John A.
2012.
Long run behaviour of the autocovariance function of ARCH(∞) models.
Journal of Mathematical Analysis and Applications,
Vol. 392,
Issue. 2,
p.
148.
Conlon, Joseph G.
and
Dabkowski, Michael
2020.
Global Stability for a Class of Nonlinear PDE with Non-local Term.
Journal of Statistical Physics,
Vol. 178,
Issue. 2,
p.
420.
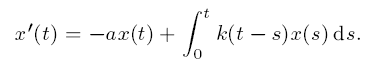 The kernel k is assumed to be positive, continuous and integrable.If
The kernel k is assumed to be positive, continuous and integrable.If
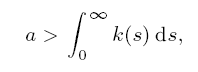 it is known that all solutions x are integrable and x(t) → 0 as t → ∞, but also that x = 0 cannot be exponentially asymptotically stable unless there is some γ > 0 such that
it is known that all solutions x are integrable and x(t) → 0 as t → ∞, but also that x = 0 cannot be exponentially asymptotically stable unless there is some γ > 0 such that
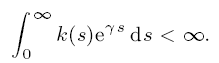 Here, we restrict the kernel to be in a class of subexponential functions in which k(t) → 0 as t → ∞ so slowly that the above condition is violated. It is proved here that the rate of convergence of x(t) → 0 as t → ∞ is given by
Here, we restrict the kernel to be in a class of subexponential functions in which k(t) → 0 as t → ∞ so slowly that the above condition is violated. It is proved here that the rate of convergence of x(t) → 0 as t → ∞ is given by
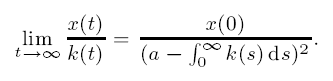 The result is proved by determining the asymptotic behaviour of the solution of the transient renewal equation
The result is proved by determining the asymptotic behaviour of the solution of the transient renewal equation
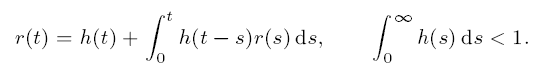 If the kernel h is subexponential, then
If the kernel h is subexponential, then