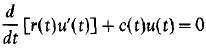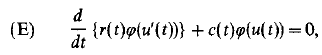Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Li, Horng-Jaan
and
Yeh, Cheh-Chih
1995.
Nonoscillation criteria for second-order half-linear differential equations.
Applied Mathematics Letters,
Vol. 8,
Issue. 5,
p.
63.
Lian, Wei-Cheng
Yeh, Cheh-Chih
and
Li, Horng-Jaan
1995.
The distance between zeros of an oscillatory solution to a half-linear differential equation.
Computers & Mathematics with Applications,
Vol. 29,
Issue. 8,
p.
39.
Došlý, Ondřej
1998.
Oscillation criteria for half-linear second order differential equations.
Hiroshima Mathematical Journal,
Vol. 28,
Issue. 3,
Kusano, Takaŝi
and
Naito, Manabu
2001.
Sturm-Liouville Eigenvalue Problems for Half- Linear Ordinary Differential Equations.
Rocky Mountain Journal of Mathematics,
Vol. 31,
Issue. 3,
Wang, Qi-Ru
2001.
Oscillation and asymptotics for second-order half-linear differential equations.
Applied Mathematics and Computation,
Vol. 122,
Issue. 2,
p.
253.
Mařı́k, Robert
2001.
A half-linear differential equation and variational problem.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 45,
Issue. 2,
p.
203.
Agarwal, Ravi P.
Grace, Said R.
and
O’Regan, Donal
2002.
Oscillation Theory for Second Order Linear, Half-Linear, Superlinear and Sublinear Dynamic Equations.
p.
93.
Luo, Jiaowan
and
Debnath, L.
2002.
Oscillation criteria for second-order quasilinear functional differential equations.
Computers & Mathematics with Applications,
Vol. 44,
Issue. 5-6,
p.
731.
Binding, Paul
and
Drábek, Pável
2003.
Sturm--Liouville theory for the p-Laplacian.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 40,
Issue. 4,
p.
373.
Tiryaki, Aydýn
Çakmak, Devrim
and
Ayanlar, Bülent
2003.
On the oscillation of certain second-order nonlinear differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 281,
Issue. 2,
p.
565.
Li, Wan-Tong
Zhong, Cheng-Kui
and
Fan, Xian-Ling
2003.
Oscillation Criteria for Second-Order Half-Linear Ordinary Differential Equations with Damping.
Rocky Mountain Journal of Mathematics,
Vol. 33,
Issue. 3,
Došlá, Zuzana
and
Vrkoč, Ivo
2004.
On an extension of the Fubini theorem and its applications in ODEs.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 57,
Issue. 4,
p.
531.
Li, Wan-Tong
2004.
Interval oscillation of second-order half-linear functional differential equations.
Applied Mathematics and Computation,
Vol. 155,
Issue. 2,
p.
451.
Wang, Qi-Ru
and
Yang, Qi-Gui
2004.
Interval criteria for oscillation of second-order half-linear differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 291,
Issue. 1,
p.
224.
2005.
Half-Linear Differential Equations.
Vol. 202,
Issue. ,
p.
471.
Özbekler, A.
and
Zafer, A.
2005.
Sturmian comparison theory for linear and half-linear impulsive differential equations.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 63,
Issue. 5-7,
p.
e289.
Tiryaki, A.
Ba¢ci, Y.
and
Güleç, I.
2005.
Interval criteria for oscillation of second-order functional differential equations.
Computers & Mathematics with Applications,
Vol. 50,
Issue. 8-9,
p.
1487.
Sugie, Jitsuro
and
Yamaoka, Naoto
2005.
Growth conditions for oscillation of nonlinear differential equations with p-Laplacian.
Journal of Mathematical Analysis and Applications,
Vol. 306,
Issue. 1,
p.
18.
Jin, Chuhua
and
Debnath, Lokenath
2007.
Oscillations of solutions of second order quasilinear differential equations with impulses.
Journal of Applied Mathematics and Computing,
Vol. 24,
Issue. 1-2,
p.
1.
Sugie, Jitsuro
Onitsuka, Masakazu
and
Yamaguchi, Aya
2007.
Asymptotic behavior of solutions of nonautonomous half-linear differential systems.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 44,
Issue. 2,
p.
159.