No CrossRef data available.
Article contents
Spaces of functions and sections with paracompact domain
Published online by Cambridge University Press: 21 November 2023
Abstract
We study spaces of continuous functions and sections with domain a paracompact Hausdorff k-space $X$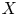 and range a nilpotent CW complex $Y$
and range a nilpotent CW complex $Y$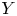 , with emphasis on localization at a set of primes. For $\mathop {\rm map}\nolimits _\phi (X,\,Y)$
, with emphasis on localization at a set of primes. For $\mathop {\rm map}\nolimits _\phi (X,\,Y)$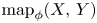 , the space of maps with prescribed restriction $\phi$
, the space of maps with prescribed restriction $\phi$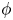 on a suitable subspace $A\subset X$
on a suitable subspace $A\subset X$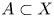 , we construct a natural spectral sequence of groups that converges to $\pi _*(\mathop {\rm map}\nolimits _\phi (X,\,Y))$
, we construct a natural spectral sequence of groups that converges to $\pi _*(\mathop {\rm map}\nolimits _\phi (X,\,Y))$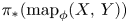 and allows for detection of localization on the level of $E^2$
and allows for detection of localization on the level of $E^2$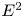 . Our applications extend and unify the previously known results.
. Our applications extend and unify the previously known results.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh



