Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-27T14:30:19.549Z Has data issue: false hasContentIssue false
  • English
  • Français

Solvability of boundary value problems for vector differential systems*

Published online by Cambridge University Press:  14 November 2011

L. H. Erbe ,
Xinzhi Liu  and
Jianhong Wu
L. H. Erbe
Affiliation:
Department of Mathematics, University of Alberta, Edmonton, Alberta, Canada, T6G 2G1
Xinzhi Liu
Affiliation:
Department of Mathematics, University of Alberta, Edmonton, Alberta, Canada, T6G 2G1
Jianhong Wu
Affiliation:
Department of Mathematics, University of Alberta, Edmonton, Alberta, Canada, T6G 2G1
Get access Rights & Permissions [Opens in a new window]

Synopsis

Brouwer topological degree theory, the shooting type method, the disconjugacy theory of Hamiltonian systems and the Liapunov-Razumikhin technique of Volterra integrodifferential equations are employed to establish some solvability results for the 2n-dimensional differential system

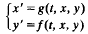
subject to one of the following boundary conditions:

(i) x(0) = Qx(l), Qg(l x(1), qy(1)= g(0, x(0), y(0)),

(ii) Blx(O) = B2g(O, x(O), y(O)), C1x(l) = −C2g(l, x(l), y(l)),

where Q, Bi, Ci, i = 1, 2, are n x n real matrices. An application is given to the second order equation xn = h(t, x, x') subject to certain nonlinear boundary conditions.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 114 , Issue 3-4 , 1990 , pp. 181 - 193
Copyright
Copyright © Royal Society of Edinburgh 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bernfeld, S. and Lakshmikantham, V.. An Introduction to Nonlinear Boundary Value Problems (New York: Academic Press, 1974).Google Scholar
2Burton, T. A.. Volterra Integral and Differential Equations (New York: Academic Press, 1983).Google Scholar
3Coppel, W. A.. Disconjugacy. Lecture Notes in Mathematics. 200 (Berlin: Springer, 1971).Google Scholar
4Erbe, L. H.. Existence of solutions to boundary value problem for second order differential equations. Nonlinear Anal. 6 (1982), 1155–1162.CrossRefGoogle Scholar
5Erbe, L. H. and Knobloch, H. W.. Boundary value problems for systems of second order differential equations. Proc. Roy. Soc. Edinburgh Sect. A 101 (1985), 61–76.CrossRefGoogle Scholar
6Erbe, L. H. and Liu, Xinzhi. Existence results for boundary value problems of second order impulsive differential equations. J. Math. Anal. Appl. (to appear).Google Scholar
7Erbe, L. H. and Schmitt, K.. On solvability of boundary value problems for systems of differential equations. J. Appl. Math. Phys. 38 (1987), 184–192.Google Scholar
8Habets, P. and Schmitt, K.. Nonlinear boundary value problems for systems of differential equation. Arch. Math. (Basel) 40 (1983), 441–446.Google Scholar
9Hartman, P.. Ordinary Differential Equations (New York: Interscience, 1964).Google Scholar
10Hartman, P.. On N-parameter families and interpolation problems for nonlinear ordinary differential equations. Trans. Amer. Math. Soc. 154 (1971), 201–226.Google Scholar
11Kelley, W. G.. Second order systems with nonlinear boundary conditions. Proc. Amer. Math. Soc. 62 (1977), 287–292.Google Scholar
12Knobloch, H. W.. Boundary value problems for systems of nonlinear differential equations. In Proc. EquadifflV, 1977, pp. 197–204. Lecture Notes in Mathematics 703 (Berlin: Springer 1978).Google Scholar
13Knobloch, H. W. and Schmitt, K.. Nonlinear boundary value problems for systems of differential equations. Proc. Roy. Soc. Edinburgh Sect. A 78(1977), 139–158.CrossRefGoogle Scholar
14Lakshmikantham, V. and Leela, S.. Differential and Integral Inequalities (New York: Academic Press, 1969).Google Scholar
15Lasota, A. and Yorke, J. A.. Existence of solutions of two-point boundary value problems for nonlinear systems. J. Differential Equations 11 (1972), 509–518.CrossRefGoogle Scholar
16Mawhin, J. and Schmidt, K.. Upper and lower solutions and semilinear second order elliptic equations with nonlinear boundary conditions. Proc. roy. Soc. Edinburgh Sect. A 97 (1984), 199–207.CrossRefGoogle Scholar
17Miller, R. K.. Nonlinear Volterra Integral Equations (New York: Benjamin, 1971).Google Scholar
18Schmitt, K.. Periodic solutions of systems of second order differential equations. J. Differential Equations 11 (1972), 180–192.Google Scholar
19Wu, Jianhong. Periodic solutions of nonconvolution neutral integrodifferential equations. Ada Math. Sci. (English Ed.) 8:3 (1988), 307–314.Google Scholar