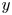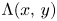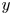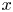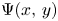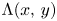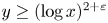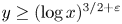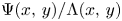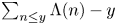1. Introduction
A positive integer is called $y$![]() -smooth if each of its prime factors does not exceed $y$
-smooth if each of its prime factors does not exceed $y$![]() . We denote the number of $y$
. We denote the number of $y$![]() -smooth integers not exceeding $x$
-smooth integers not exceeding $x$![]() by $\Psi (x,\,y)$
by $\Psi (x,\,y)$![]() . We assume throughout $x \ge y \ge 2$
. We assume throughout $x \ge y \ge 2$![]() . Let $\rho \colon [0,\,\infty ) \to (0,\,\infty )$
. Let $\rho \colon [0,\,\infty ) \to (0,\,\infty )$![]() be the Dickman function, defined as $\rho (t)=1$
be the Dickman function, defined as $\rho (t)=1$![]() for $t \in [0,\,1]$
for $t \in [0,\,1]$![]() and via the delay differential equation $t \rho '(t) =-\rho (t-1)$
and via the delay differential equation $t \rho '(t) =-\rho (t-1)$![]() for $t>1$
for $t>1$![]() . Dickman [Reference Dickman7] showed that
. Dickman [Reference Dickman7] showed that
holds when $y \ge x^{\varepsilon }$![]() . For this reason, it is useful to introduce
. For this reason, it is useful to introduce
De Bruijn [Reference de Bruijn3, Eqs. (1.3), (4.6)] showed that
when $x \to \infty$![]() and $(\log x)/2 >\log y > (\log x)^{5/8}$
and $(\log x)/2 >\log y > (\log x)^{5/8}$![]() . Here and later $\gamma$
. Here and later $\gamma$![]() is the Euler–Mascheroni constant. As we see, there is no arithmetic information in the leading behaviour of the error term $\Psi (x,\,y) - x \rho (u)$
is the Euler–Mascheroni constant. As we see, there is no arithmetic information in the leading behaviour of the error term $\Psi (x,\,y) - x \rho (u)$![]() , and in particular it does not oscillate. Moreover, the error term is large: the saving (1.2) gives over the main term is merely $\asymp \log (u+1)/\log y$
, and in particular it does not oscillate. Moreover, the error term is large: the saving (1.2) gives over the main term is merely $\asymp \log (u+1)/\log y$![]() [Reference de Bruijn3, p. 56].
[Reference de Bruijn3, p. 56].
This begs the question, what is the correct main term for $\Psi (x,\,y)$![]() that leads to a small and arithmetically rich error term? De Bruijn [Reference de Bruijn3, Eq. (2.9)] introduced a refinement of $\rho$
that leads to a small and arithmetically rich error term? De Bruijn [Reference de Bruijn3, Eq. (2.9)] introduced a refinement of $\rho$![]() , often denoted $\lambda _y$
, often denoted $\lambda _y$![]() :
:
if $y^u \notin \mathbb {Z}$![]() ; otherwise $\lambda _y(u)=\lambda _y(u+)$
; otherwise $\lambda _y(u)=\lambda _y(u+)$![]() (one has $\lambda _y(u)= \lambda _y(u-)+O(1/x)$
(one has $\lambda _y(u)= \lambda _y(u-)+O(1/x)$![]() if $y^u \in \mathbb {Z}$
if $y^u \in \mathbb {Z}$![]() [Reference de Bruijn3, p. 54]). The count $\Psi (x,\,y)$
[Reference de Bruijn3, p. 54]). The count $\Psi (x,\,y)$![]() should be compared to
should be compared to
We refer the reader to de Bruijn's original paper for the motivation for this definition. In particular, $\Lambda$![]() satisfies the following continuous variant of Buchstab's identity:
satisfies the following continuous variant of Buchstab's identity:
for $y \le z$![]() , to be compared with $\Psi (x,\,y)=\Psi (x,\,z)-\sum _{y < p \le z}\Psi (x/p,\,p)$
, to be compared with $\Psi (x,\,y)=\Psi (x,\,z)-\sum _{y < p \le z}\Psi (x/p,\,p)$![]() . De Bruijn proved [Reference de Bruijn3, Eq. (1.4)]
. De Bruijn proved [Reference de Bruijn3, Eq. (1.4)]
holds for $\log y > \sqrt {\log x}$![]() . Saias [Reference Saias17, Lem. 4] improved the range to $y \ge (\log x)^{1+\varepsilon }$
. Saias [Reference Saias17, Lem. 4] improved the range to $y \ge (\log x)^{1+\varepsilon }$![]() . De Bruijn and Saias also provided asymptotic series expansion for $\lambda _y(u)$
. De Bruijn and Saias also provided asymptotic series expansion for $\lambda _y(u)$![]() in (roughly) powers of $\log (u+1)/\log y$
in (roughly) powers of $\log (u+1)/\log y$![]() . Hildebrand and Tenenbaum [Reference Hildebrand and Tenenbaum14, Lem. 3.1] showed that for $y \ge (\log x)^{1+\varepsilon }$
. Hildebrand and Tenenbaum [Reference Hildebrand and Tenenbaum14, Lem. 3.1] showed that for $y \ge (\log x)^{1+\varepsilon }$![]() ,
,
for $y \ge (\log x)^{1+\varepsilon }$![]() . Implicit in the proof of proposition 4.1 of La Bretèche and Tenenbaum [Reference de la Bretèche and Tenenbaum5] is the estimate
. Implicit in the proof of proposition 4.1 of La Bretèche and Tenenbaum [Reference de la Bretèche and Tenenbaum5] is the estimate
for $y \ge (\log x)^{1+\varepsilon }$![]() where $\zeta$
where $\zeta$![]() is the Riemann zeta function and $\xi \colon [1,\,\infty ) \to [0,\,\infty )$
is the Riemann zeta function and $\xi \colon [1,\,\infty ) \to [0,\,\infty )$![]() is defined via
is defined via
We include as an appendix a proof in English of (1.5). The function $K$![]() originates in de Bruijn's work [Reference de Bruijn3, Eq. (2.8)]. Evidently, $K(0)=1$
originates in de Bruijn's work [Reference de Bruijn3, Eq. (2.8)]. Evidently, $K(0)=1$![]() and $\lim _{t \to -1^+} K(t)= \infty$
and $\lim _{t \to -1^+} K(t)= \infty$![]() . Moreover, $K$
. Moreover, $K$![]() is strictly decreasing in $(-1,\,0]$
is strictly decreasing in $(-1,\,0]$![]() [Reference Gorodetsky9].
[Reference Gorodetsky9].
Suppose $\pi (x)=\mathrm {Li}(x)(1+O(\exp (-(\log x)^{a})))$![]() for some $a \in (0,\,1)$
for some $a \in (0,\,1)$![]() . Saias [Reference Saias17, Thm.], improving on De Bruijn [Reference de Bruijn3], proved that
. Saias [Reference Saias17, Thm.], improving on De Bruijn [Reference de Bruijn3], proved that
holds in the range $\log y \ge (\log \log x)^{{1}/{a}+\varepsilon }$![]() . By the Vinogradov–Korobov zero-free region, we may take $a=3/5$
. By the Vinogradov–Korobov zero-free region, we may take $a=3/5$![]() . Saias writes without proof [Reference Saias17, p. 81] that under the Riemann hypothesis (RH) his methods give
. Saias writes without proof [Reference Saias17, p. 81] that under the Riemann hypothesis (RH) his methods give
in the range $y \ge (\log x)^{2+\varepsilon }$![]() , which recovers a conditional result of Hildebrand [Reference Hildebrand11].
, which recovers a conditional result of Hildebrand [Reference Hildebrand11].
1.1 $G$
Define the entire function $I(s)=\int _{0}^{s} \tfrac {e^v-1}{v}\,{\rm d}v$![]() . As shown in [Reference Hildebrand and Tenenbaum14, Lem. 2.6], the Laplace transform of $\rho$
. As shown in [Reference Hildebrand and Tenenbaum14, Lem. 2.6], the Laplace transform of $\rho$![]() is
is
for all $s \in \mathbb {C}$![]() . In [Reference Gorodetsky9] we studied in detail the ratio
. In [Reference Gorodetsky9] we studied in detail the ratio
where
is the partial zeta function and
The function $G(s,\,y)$![]() is defined for $\Re s>0$
is defined for $\Re s>0$![]() such that $\zeta (s) \neq 0$
such that $\zeta (s) \neq 0$![]() . Informally, $G$
. Informally, $G$![]() carries information about the ratio $\Psi (x,\,y)/\Lambda (x,\,y)$
carries information about the ratio $\Psi (x,\,y)/\Lambda (x,\,y)$![]() , since $s\mapsto \zeta (s,\,y)/s$
, since $s\mapsto \zeta (s,\,y)/s$![]() is the Mellin transform of $x\mapsto \Psi (x,\,y)$
is the Mellin transform of $x\mapsto \Psi (x,\,y)$![]() while $s\mapsto F(s,\,y)/s$
while $s\mapsto F(s,\,y)/s$![]() is the Mellin transform of $x\mapsto \Lambda (x,\,y)$
is the Mellin transform of $x\mapsto \Lambda (x,\,y)$![]() [Reference de Bruijn3, p. 54]. As in [Reference Gorodetsky9], it is essential to write $G$
[Reference de Bruijn3, p. 54]. As in [Reference Gorodetsky9], it is essential to write $G$![]() as $G_1 G_2$
as $G_1 G_2$![]() where
where

We assume $\log \zeta (s)$![]() is chosen to be real when $s>1$
is chosen to be real when $s>1$![]() .
.
1.2 Main results
Let $\psi (y)=\sum _{n \le y}\Lambda (n)$![]() and
and
Theorem 1.1 Assume RH. Fix $\varepsilon \in (0,\,1)$![]() . Suppose that $x \ge C_{\varepsilon}$
. Suppose that $x \ge C_{\varepsilon}$![]() and $x^{1-\varepsilon } \ge y \ge (\log x)^{2+\varepsilon }$
and $x^{1-\varepsilon } \ge y \ge (\log x)^{2+\varepsilon }$![]() . Then
. Then
The following theorem gives an asymptotic formula for $\Psi (x,\,y)$![]() for $y$
for $y$![]() smaller than $(\log x)^{2}$
smaller than $(\log x)^{2}$![]() .
.
Theorem 1.2 Assume RH. Fix $\varepsilon \in (0,\,1/3)$![]() . Suppose that $x \ge C_{\varepsilon}$
. Suppose that $x \ge C_{\varepsilon}$![]() and $(\log x)^{3} \ge y \ge (\log x)^{4/3+\varepsilon }$
and $(\log x)^{3} \ge y \ge (\log x)^{4/3+\varepsilon }$![]() . Then
. Then
If $y \le (\log x)^{2-\varepsilon }$![]() then the error term can be improved to $O_{\varepsilon } ((\log x)^3/(y^2 \log y))$
then the error term can be improved to $O_{\varepsilon } ((\log x)^3/(y^2 \log y))$![]() .
.
Theorems 1.1 and 1.2, proved in § 4, show that
holds when $y/((\log x)^{3/2}(\log \log x)^{-1/2}) \to \infty$![]() . This range is shown to be optimal in Theorem 2.14 of [Reference Gorodetsky9]. The same theorem also supplies an alternative proof of theorem 1.2 when $y \le (\log x)^{2-\varepsilon }$
. This range is shown to be optimal in Theorem 2.14 of [Reference Gorodetsky9]. The same theorem also supplies an alternative proof of theorem 1.2 when $y \le (\log x)^{2-\varepsilon }$![]() (the proof can be adapted to cover $(\log x)^{2-\varepsilon } \le y \le (\log x)^3$
(the proof can be adapted to cover $(\log x)^{2-\varepsilon } \le y \le (\log x)^3$![]() as well).
as well).
Hildebrand showed that RH is equivalent to $\Psi (x,\,y) \asymp _{\varepsilon } x\rho (u)$![]() for $y \ge (\log x)^{2+\varepsilon }$
for $y \ge (\log x)^{2+\varepsilon }$![]() [Reference Hildebrand11]. He conjectured that $\Psi (x,\,y)$
[Reference Hildebrand11]. He conjectured that $\Psi (x,\,y)$![]() is not of size $\asymp x\rho (u)$
is not of size $\asymp x\rho (u)$![]() when $y \le (\log x)^{2-\varepsilon }$
when $y \le (\log x)^{2-\varepsilon }$![]() [Reference Hildebrand12]. This was recently confirmed by the author [Reference Gorodetsky9]. This also follows (under RH) from theorem 1.2, since $\Lambda (x,\,y) \asymp _{\varepsilon } x\rho (u)$
[Reference Hildebrand12]. This was recently confirmed by the author [Reference Gorodetsky9]. This also follows (under RH) from theorem 1.2, since $\Lambda (x,\,y) \asymp _{\varepsilon } x\rho (u)$![]() for $y \ge (\log x)^{1+\varepsilon }$
for $y \ge (\log x)^{1+\varepsilon }$![]() while (under RH) $G(\beta,\,y) \to \infty$
while (under RH) $G(\beta,\,y) \to \infty$![]() when $y \le (\log x)^{2-\varepsilon }$
when $y \le (\log x)^{2-\varepsilon }$![]() and $x \to \infty$
and $x \to \infty$![]() (this follows from the estimates for $G$
(this follows from the estimates for $G$![]() in [Reference Gorodetsky9], see § 2).
in [Reference Gorodetsky9], see § 2).
Theorems 1.1 and 1.2 and their proofs have their origin in our work in the polynomial setting [Reference Gorodetsky10], where $\Psi (x,\,y)$![]() corresponds to the number of $m$
corresponds to the number of $m$![]() -smooth polynomials of degree $n$
-smooth polynomials of degree $n$![]() over a finite field, while $\Lambda (x,\,y)$
over a finite field, while $\Lambda (x,\,y)$![]() is analogous to the number of $m$
is analogous to the number of $m$![]() -smooth permutations of $S_n$
-smooth permutations of $S_n$![]() (multiplied by $q^n/n!$
(multiplied by $q^n/n!$![]() ). In that setting, the analogue of $G_1(s,\,y)$
). In that setting, the analogue of $G_1(s,\,y)$![]() is identically $1$
is identically $1$![]() (the relevant zeta function has no zeros) which makes the analysis unconditional.
(the relevant zeta function has no zeros) which makes the analysis unconditional.
1.3 Applications: sign changes and biases
From theorem 1.1 we deduce in § 2.2 the following
Corollary 1.3 Assume RH. Fix $\varepsilon \in (0,\,1)$![]() . Suppose that $x\ge C_{\varepsilon}$
. Suppose that $x\ge C_{\varepsilon}$![]() and $x^{1-\varepsilon } \ge y \ge (\log x)^{2+\varepsilon }$
and $x^{1-\varepsilon } \ge y \ge (\log x)^{2+\varepsilon }$![]() . Then
. Then

holds for $T \ge 4$![]() , where the sum is over zeros of $\zeta$
, where the sum is over zeros of $\zeta$![]() .
.
Corollary 1.3 implies that large positive (resp. negative) values of $\psi (y)-y$![]() lead to large positive (resp. negative) values of $\Psi (x,\,y) -\Lambda (x,\,y)$
lead to large positive (resp. negative) values of $\Psi (x,\,y) -\Lambda (x,\,y)$![]() and vice versa. Large and small values of $\psi (y)-y$
and vice versa. Large and small values of $\psi (y)-y$![]() were exhibited by Littlewood [Reference Montgomery and Vaughan15, Thm. 15.11]. Note that corollary 1.3 sharpens (1.7) if $y \le x^{1-\varepsilon }$
were exhibited by Littlewood [Reference Montgomery and Vaughan15, Thm. 15.11]. Note that corollary 1.3 sharpens (1.7) if $y \le x^{1-\varepsilon }$![]() .Footnote 1
.Footnote 1
Let $\pi (x)$![]() be the count of primes up to $x$
be the count of primes up to $x$![]() and $\mathrm {Li}(x)$
and $\mathrm {Li}(x)$![]() be the logarithmic integral. It is known that $\pi (x)-\mathrm {Li}(x)$
be the logarithmic integral. It is known that $\pi (x)-\mathrm {Li}(x)$![]() is biased towards positive values in the following sense. Assuming RH and the Linear Independence hypothesis (LI) for zeros of $\zeta$
is biased towards positive values in the following sense. Assuming RH and the Linear Independence hypothesis (LI) for zeros of $\zeta$![]() , Rubinstein and Sarnak [Reference Rubinstein and Sarnak16] showed that the set
, Rubinstein and Sarnak [Reference Rubinstein and Sarnak16] showed that the set
has logarithmic density $\approx 0.999997$![]() . This is an Archimedean analogue of the classical Chebyshev's bias on primes in arithmetic progressions. We use corollary 1.3 to exhibit a similar bias for smooth integers. Let us fix the value of $\beta =1-\xi (u)/\log y$
. This is an Archimedean analogue of the classical Chebyshev's bias on primes in arithmetic progressions. We use corollary 1.3 to exhibit a similar bias for smooth integers. Let us fix the value of $\beta =1-\xi (u)/\log y$![]() to be
to be
where $\beta _0 \in (1/2,\,1)$![]() . This amounts to restricting $x$
. This amounts to restricting $x$![]() to be a function $x=x(y)$
to be a function $x=x(y)$![]() of $y$
of $y$![]() defined by
defined by
In particular, $y=(\log x)^{1/(1-\beta _0)+o(1)}$![]() . Then corollary 1.3 shows
. Then corollary 1.3 shows

Applying the formalism of Akbary et al. [Reference Akbary, Ng and Shahabi1] to the right-hand side of (1.14) we deduce immediately
Corollary 1.4 Assume RH. Assume LI for $\zeta$![]() . Fix $\beta _0 \in (1/2,\,1)$
. Fix $\beta _0 \in (1/2,\,1)$![]() and let $x$
and let $x$![]() be a function of $y$
be a function of $y$![]() defined as in (1.13). Then the set
defined as in (1.13). Then the set
has logarithmic density greater than $1/2$![]() , and the left-hand side of (1.14) has a limiting distribution in logarithmic sense.
, and the left-hand side of (1.14) has a limiting distribution in logarithmic sense.
In the same way that Chebyshev's bias for primes relates to the contribution of prime squares, this is also the case for smooth integers. Writing $G$![]() as $G_1 G_2$
as $G_1 G_2$![]() as in § 1.1, $G_2$
as in § 1.1, $G_2$![]() captures the contribution of proper powers of primes. When $\beta _0 \in (1/2,\,1)$
captures the contribution of proper powers of primes. When $\beta _0 \in (1/2,\,1)$![]() , the only significant term in $G_2(\beta _0,\,y)$
, the only significant term in $G_2(\beta _0,\,y)$![]() is $k=2$
is $k=2$![]() , which corresponds to squares of primes. The squares lead to the term $y^{1/2}/(2\beta _0-1)$
, which corresponds to squares of primes. The squares lead to the term $y^{1/2}/(2\beta _0-1)$![]() in (1.14) which creates the bias.
in (1.14) which creates the bias.
Remark 1.5 Consider the arithmetic function $\alpha _y(n)$![]() defined implicitly via
defined implicitly via

This function is supported on $y$![]() -smooth numbers and coincides with the indicator of $y$
-smooth numbers and coincides with the indicator of $y$![]() -smooth numbers on squarefree integers. Working with the summatory function of $\alpha _y$
-smooth numbers on squarefree integers. Working with the summatory function of $\alpha _y$![]() instead of $\Psi (x,\,y)$
instead of $\Psi (x,\,y)$![]() , the bias discussed above disappears. This is because, modifying the proof of theorem 1.1, one finds that
, the bias discussed above disappears. This is because, modifying the proof of theorem 1.1, one finds that

holds in $x^{1-\varepsilon } \ge y \ge (\log x)^{2+\varepsilon }$![]() , meaning the bias-causing factor $G_2(\beta,\,y)$
, meaning the bias-causing factor $G_2(\beta,\,y)$![]() does not arise. This is analogous to how the indicator function of primes is biased, while $\Lambda (n)/\log n$
does not arise. This is analogous to how the indicator function of primes is biased, while $\Lambda (n)/\log n$![]() is not.
is not.
Remark 1.6 It is interesting to see if one can formulate and prove variants of corollaries 1.3 and 1.4 in the range $y \le (\log x)^{1-\varepsilon }$![]() . In this range, an accurate main term for $\Psi (x,\,y)$
. In this range, an accurate main term for $\Psi (x,\,y)$![]() was established in [Reference de la Bretèche and Tenenbaum6].
was established in [Reference de la Bretèche and Tenenbaum6].
1.4 Strategy behind theorems 1.1 and 1.2
We write $\Psi (x,\,y)$![]() as a Perron integral, at least for non-integer $x$
as a Perron integral, at least for non-integer $x$![]() :
:
where $\sigma$![]() can be any positive real. For non-integer $x$
can be any positive real. For non-integer $x$![]() we also have
we also have
whenever $\sigma >\varepsilon$![]() and $y \ge C_{\varepsilon}$
and $y \ge C_{\varepsilon}$![]() . Indeed, the Laplace inversion formula expresses $\Lambda (x,\,y)$
. Indeed, the Laplace inversion formula expresses $\Lambda (x,\,y)$![]() as
as

for any $c$![]() such that
such that
converges absolutely for $\Re s \ge c$![]() . In particular, we may take $c>-(\log y)/(1+\varepsilon )$
. In particular, we may take $c>-(\log y)/(1+\varepsilon )$![]() if we assume $y\ge C_{\varepsilon}$
if we assume $y\ge C_{\varepsilon}$![]() , as Saias showed, see corollary A.2. As shown by de Bruijn [Reference de Bruijn3, Eq. (2.6)] (cf. [Reference Saias17, Lem. 6]),
, as Saias showed, see corollary A.2. As shown by de Bruijn [Reference de Bruijn3, Eq. (2.6)] (cf. [Reference Saias17, Lem. 6]),
By definition of $F$![]() , (1.9), we can rewrite (1.16) as (1.15). As Saias does, we choose to work with $\sigma =\beta$
, (1.9), we can rewrite (1.16) as (1.15). As Saias does, we choose to work with $\sigma =\beta$![]() , which is essentially a saddle point for $F(s,\,y)x^s$
, which is essentially a saddle point for $F(s,\,y)x^s$![]() . If $x \ge y \ge (\log x)^{1+\varepsilon }$
. If $x \ge y \ge (\log x)^{1+\varepsilon }$![]() and $x \ge C_{\varepsilon}$
and $x \ge C_{\varepsilon}$![]() then lemma 2.1 implies
then lemma 2.1 implies
Saias proved (1.6) by showing that $\zeta (s,\,y)$![]() and $F(s,\,y)$
and $F(s,\,y)$![]() are close and so if we subtract
are close and so if we subtract
then we can bound the integral by using pointwise bounds for the integrand. Instead of subtracting $\Lambda (x,\,y)$![]() , we subtract $\Lambda (x,\,y)$
, we subtract $\Lambda (x,\,y)$![]() times $G(\beta,\,y)$
times $G(\beta,\,y)$![]() , which leads to
, which leads to

We want to bound the integral in (1.18). The proof of theorem 1.1 considers separately the range
and its complement. When $u$![]() satisfies (1.19), then in (1.18) one needs only small values of $\Re s$
satisfies (1.19), then in (1.18) one needs only small values of $\Re s$![]() to estimate the integral ($|\Re s| \le 1/\log y$
to estimate the integral ($|\Re s| \le 1/\log y$![]() ) with arbitrary power saving in $y$
) with arbitrary power saving in $y$![]() . This is an unconditional observation established in proposition 3.1. However, for smaller $u$
. This is an unconditional observation established in proposition 3.1. However, for smaller $u$![]() , one needs $|\Re s|$
, one needs $|\Re s|$![]() going up to a power of $y$
going up to a power of $y$![]() if one desires power saving in $y$
if one desires power saving in $y$![]() , which makes the proof more involved.
, which makes the proof more involved.
In our proofs, RH is only invoked at the very end to estimate $G_1$![]() and its derivatives. For instance, in the range where (1.19) and $y \ge (\log x)^{2+\varepsilon }$
and its derivatives. For instance, in the range where (1.19) and $y \ge (\log x)^{2+\varepsilon }$![]() hold, we prove in (4.12) the unconditional estimate
hold, we prove in (4.12) the unconditional estimate

See (4.16) for a similar estimate for $u \le (\log y)(\log \log y)^3$![]() . In particular, our proofs are easily modified to recover (1.6).
. In particular, our proofs are easily modified to recover (1.6).
Conventions
The letters $C,\,c$![]() denote absolute positive constants that may change between different occurrences. We denote by $C_{\varepsilon },\,c_{\varepsilon }$
denote absolute positive constants that may change between different occurrences. We denote by $C_{\varepsilon },\,c_{\varepsilon }$![]() positive constants depending only on $\varepsilon$
positive constants depending only on $\varepsilon$![]() , which may also change between different occurrences. The notation $A \ll B$
, which may also change between different occurrences. The notation $A \ll B$![]() means $|A| \le C B$
means $|A| \le C B$![]() for some absolute constant $C$
for some absolute constant $C$![]() , and $A\ll _{\varepsilon } B$
, and $A\ll _{\varepsilon } B$![]() means $|A| \le C_{\varepsilon } B$
means $|A| \le C_{\varepsilon } B$![]() . We write $A \asymp B$
. We write $A \asymp B$![]() to mean $C_1 B \le A \le C_2 B$
to mean $C_1 B \le A \le C_2 B$![]() for some absolute positive constants $C_i$
for some absolute positive constants $C_i$![]() , and $A \asymp _{\varepsilon } B$
, and $A \asymp _{\varepsilon } B$![]() means $C_i$
means $C_i$![]() may depend on $\varepsilon$
may depend on $\varepsilon$![]() . The letter $\rho$
. The letter $\rho$![]() will always indicate a non-trivial zero of $\zeta$
will always indicate a non-trivial zero of $\zeta$![]() . When we differentiate a bivariate function, we always do so with respect to the first variable. We set
. When we differentiate a bivariate function, we always do so with respect to the first variable. We set
2. Preliminaries
2.1 Standard lemmas
Recall $\beta$![]() was defined in (1.10).
was defined in (1.10).
Lemma 2.1 [Reference Hildebrand and Tenenbaum13, Lem. 1] For $u \ge 3$![]() we have $\xi (u) = \log u + \log \log u + O( (\log \log u) / \log u)$
we have $\xi (u) = \log u + \log \log u + O( (\log \log u) / \log u)$![]() . In particular,
. In particular,
Lemma 2.2 [Reference de Bruijn2]
For $u \ge 1$![]() we have $\rho (u) \asymp e^{-u\xi +I(\xi )} u^{-1/2} = x^{\beta -1} e^{I(\xi )}u^{-1/2}$
we have $\rho (u) \asymp e^{-u\xi +I(\xi )} u^{-1/2} = x^{\beta -1} e^{I(\xi )}u^{-1/2}$![]() .
.
In the next lemmas we write $s \in \mathbb {C}$![]() as $s=\sigma + it$
as $s=\sigma + it$![]() .
.
Lemma 2.3 [Reference Montgomery and Vaughan15, Cor. 10.5] For $|\sigma | \le A$![]() and $|t| \ge 1$
and $|t| \ge 1$![]() , $|\zeta (s)| \asymp _A (|t|+4)^{1/2-\sigma }|\zeta (1-s)|$
, $|\zeta (s)| \asymp _A (|t|+4)^{1/2-\sigma }|\zeta (1-s)|$![]() .
.
Lemma 2.4 [Reference Montgomery and Vaughan15, Cor. 1.17] Fix $\varepsilon >0$![]() . For $\sigma \in [\varepsilon,\,2]$
. For $\sigma \in [\varepsilon,\,2]$![]() and $|t| \ge 1$
and $|t| \ge 1$![]() we have
we have
Lemma 2.5 [Reference Titchmarsh19, Thm. 7.2(A)]
We have, for $\sigma \in [1/2,\,2]$![]() and $T \ge 2$
and $T \ge 2$![]() ,
,

Lemma 2.6 [Reference Hildebrand and Tenenbaum14, Lem. 2.7] The following bounds hold for $s=-\xi (u)+it$![]() :
:

The third case of lemma 2.6 is usually stated in the range $1+u\xi \le |t|$![]() , but the same proof works for $1+u\xi = O(|t|)$
, but the same proof works for $1+u\xi = O(|t|)$![]() . Since $1+u\xi =e^{\xi }$
. Since $1+u\xi =e^{\xi }$![]() , the third case can also be written as
, the third case can also be written as
for $s=\sigma +it$![]() , assuming $\sigma <0$
, assuming $\sigma <0$![]() and $e^{-\sigma } =O(|t|)$
and $e^{-\sigma } =O(|t|)$![]() . The following lemma is a variant of [Reference Hildebrand and Tenenbaum13, Lem. 8], proved in the same way.
. The following lemma is a variant of [Reference Hildebrand and Tenenbaum13, Lem. 8], proved in the same way.
Lemma 2.7 [Reference Hildebrand and Tenenbaum13]
Fix $\varepsilon >0$![]() . Suppose $x \ge y \ge (\log x)^{1+\varepsilon }$
. Suppose $x \ge y \ge (\log x)^{1+\varepsilon }$![]() and $x \ge C_{\varepsilon}$
and $x \ge C_{\varepsilon}$![]() . For $|t| \le 1/\log y$
. For $|t| \le 1/\log y$![]() ,
,
For $1/\log y \le |t| \le \exp ((\log y)^{3/2-\varepsilon })$![]() ,
,
2.2 More on $G$
Lemma 2.8 [Reference Gorodetsky9]
Fix $0 \le i \le 4$![]() . Let $y \ge 4$
. Let $y \ge 4$![]() . Let $s \in \mathbb {C}$
. Let $s \in \mathbb {C}$![]() with $\Re s \in [0,\,1]$
with $\Re s \in [0,\,1]$![]() and the property that
and the property that
Then for $T \ge 3+|\Im s|$![]() we have
we have

Corollary 2.9 Fix $0 \le i \le 4$![]() . Let $y \ge 4$
. Let $y \ge 4$![]() . Let $s \in \mathbb {C}$
. Let $s \in \mathbb {C}$![]() with $\Re s \in [0,\,1]$
with $\Re s \in [0,\,1]$![]() . If $|\Im s| \le 1$
. If $|\Im s| \le 1$![]() we have $(\log G_1)^{(i)}(s,\,y) \ll L(y)^{-c} y^{1-\Re s}$
we have $(\log G_1)^{(i)}(s,\,y) \ll L(y)^{-c} y^{1-\Re s}$![]() unconditionally. Under RH, if $T \ge 4$
unconditionally. Under RH, if $T \ge 4$![]() and $|\Im s| \le 1$
and $|\Im s| \le 1$![]() then
then

Under RH, if $T \ge 4$![]() , $\Re s \in [3/4,\,1]$
, $\Re s \in [3/4,\,1]$![]() and $|\Im s| \le y^{9/10}$
and $|\Im s| \le y^{9/10}$![]() then
then

Proof. If $|\Im s| \le 1$![]() then (2.5) holds. It is easily seen that, for any zero $\rho$
then (2.5) holds. It is easily seen that, for any zero $\rho$![]() of $\zeta$
of $\zeta$![]() ,
,
if (2.5) holds. We apply lemma 2.8 with $T=L(y)^c$![]() and use the Vinogradov–Korobov zero-free region and (2.9) to simplify. Now assume RH, i.e. $|y^{\rho }|=y^{1/2}$
and use the Vinogradov–Korobov zero-free region and (2.9) to simplify. Now assume RH, i.e. $|y^{\rho }|=y^{1/2}$![]() . We demonstrate (2.7), and (2.8) is proved along similar lines. We apply lemma 2.8 with $T\ge 4$
. We demonstrate (2.7), and (2.8) is proved along similar lines. We apply lemma 2.8 with $T\ge 4$![]() and simplify it using (2.9). We bound the resulting error using the facts $\min _{t \ge 0}|\rho -s-t| \asymp |\rho -s|$
and simplify it using (2.9). We bound the resulting error using the facts $\min _{t \ge 0}|\rho -s-t| \asymp |\rho -s|$![]() and $\sum _{\rho } 1/|\rho -s|^2 \ll 1$
and $\sum _{\rho } 1/|\rho -s|^2 \ll 1$![]() for $|s|\le 2$
for $|s|\le 2$![]() , since there are $\ll \log T$
, since there are $\ll \log T$![]() zeros of $\zeta$
zeros of $\zeta$![]() between height $T$
between height $T$![]() and $T+1$
and $T+1$![]() [Reference Montgomery and Vaughan15, Thm. 10.13]. This gives the first equality in (2.7). The second equality in (2.7) follows by taking $T=y$
[Reference Montgomery and Vaughan15, Thm. 10.13]. This gives the first equality in (2.7). The second equality in (2.7) follows by taking $T=y$![]() , recalling the classical estimate
, recalling the classical estimate

given in [Reference Montgomery and Vaughan15, Thm. 12.5] (it also follows from lemma 2.8 with $(i,\,s,\,T)=(1,\,0,\,y)$![]() ), and the bound $\sum _{\rho } 1/(|\rho -s||\rho |) \ll 1$
), and the bound $\sum _{\rho } 1/(|\rho -s||\rho |) \ll 1$![]() . The last inequality in (2.7) is von Koch's bound $\psi (y)-y=O(y^{1/2}\log ^2 y)$
. The last inequality in (2.7) is von Koch's bound $\psi (y)-y=O(y^{1/2}\log ^2 y)$![]() [Reference von Koch20].
[Reference von Koch20].
We turn to $G_2$![]() . By the non-negativity of the coefficients of $\log G_2$
. By the non-negativity of the coefficients of $\log G_2$![]() , for $i \ge 0$
, for $i \ge 0$![]() and $\Re s>0$
and $\Re s>0$![]() we have
we have
Lemma 2.10 [Reference Gorodetsky9]
Fix $\varepsilon >0$![]() and $0 \le i \le 4$
and $0 \le i \le 4$![]() . For $y \ge 2$
. For $y \ge 2$![]() and $1 \ge s \ge \varepsilon$
and $1 \ge s \ge \varepsilon$![]() ,
,

Corollary 2.9 and lemma 2.10, applied with $i=0$![]() , imply the following
, imply the following
Lemma 2.11 Assume RH. Fix $\varepsilon >0$![]() . If $1 \ge s \ge 1/2+\varepsilon$
. If $1 \ge s \ge 1/2+\varepsilon$![]() and $T \ge 4$
and $T \ge 4$![]() then
then

Corollary 1.3 follows from theorem 1.1 by simplifying $G(\beta,\,y)$![]() using lemma 2.11 and (2.1).
using lemma 2.11 and (2.1).
3. Truncation estimates for $\Psi$ and $\Lambda$
and $\Lambda$
The purpose of this section is to prove the following two propositions.
Proposition 3.1 Medium $u$
Suppose $x \ge y \ge 2$![]() satisfy
satisfy
Fix $\varepsilon >0$![]() . Suppose $y \ge (\log x)^{1+\varepsilon }$
. Suppose $y \ge (\log x)^{1+\varepsilon }$![]() and $x \ge C_{\varepsilon}$
and $x \ge C_{\varepsilon}$![]() . Then
. Then


Proposition 3.2 Small $u$
Suppose $x \ge y \ge 2$![]() satisfy
satisfy
Suppose $x \ge C$![]() and let $T \in [(\log x)^5,\,x\rho (u)]$
and let $T \in [(\log x)^5,\,x\rho (u)]$![]() . Then
. Then

3.1 Preparation
Lemma 3.3 Fix $\varepsilon \in (0,\,1)$![]() . For $\sigma \in [\varepsilon,\,1]$
. For $\sigma \in [\varepsilon,\,1]$![]() and $x \ge T \ge 2$
and $x \ge T \ge 2$![]() we have
we have
The integral should be understood in principal value sense. Lemma 3.3 makes more precise a computation done in p. 96 of Saias’ paper [Reference Saias17] (cf. [Reference Tenenbaum18, p. 537]), which is not stated for general $T$![]() and $\sigma$
and $\sigma$![]() but contains the same ideas.
but contains the same ideas.
Proof. By [Reference Titchmarsh19, Thm. 4.11], for every $r>0$![]() we have
we have

as long as $s \neq 1$![]() , $\Re s \ge \varepsilon$
, $\Re s \ge \varepsilon$![]() and $|\Im s|\le 2r$
and $|\Im s|\le 2r$![]() . Suppose $s=\sigma +it$
. Suppose $s=\sigma +it$![]() with $|t| \ge 1$
with $|t| \ge 1$![]() . We apply this estimate with $r=|t|$
. We apply this estimate with $r=|t|$![]() , obtaining
, obtaining

We now plug (3.4) in the left-hand side of (3.3). The contribution of the error term to the integral is acceptable:
The contribution of $n^{-s} \mathbf {1}_{n\le |t|}$![]() in (3.4) to the left-hand side of (3.3) is
in (3.4) to the left-hand side of (3.3) is
Since
by the truncated Perron's formula [Reference Hildebrand and Tenenbaum14, p. 435], and
by Perron's formula, it follows that the integral in (3.5) is bounded by
and so the total contribution of the $n$![]() -sum in (3.4) to the left-hand side of (3.3) is
-sum in (3.4) to the left-hand side of (3.3) is

It remains to estimate (3.6), which we do according to the size of $n$![]() . The contribution of $n \ge 2x$
. The contribution of $n \ge 2x$![]() is
is
The contribution of $n \in (x/2,\,2x)$![]() can be bounded by considering separately the $n$
can be bounded by considering separately the $n$![]() closest to $x$
closest to $x$![]() , and partitioning the rest of the $n$
, and partitioning the rest of the $n$![]() s according to the value of $k\ge 0$
s according to the value of $k\ge 0$![]() for which $|\log (x/n)| \in [2^{-k},\,2^{1-k})$
for which $|\log (x/n)| \in [2^{-k},\,2^{1-k})$![]() :
:

The contribution of $n \le T/2$![]() is
is

Finally, the contribution of $T/2< n\le x/2$![]() is
is

acceptable as well.
Corollary 3.4 Fix $\varepsilon \in (0,\,1)$![]() . Suppose $x \ge y \ge C_{\varepsilon}$
. Suppose $x \ge y \ge C_{\varepsilon}$![]() . For $\sigma \in [\varepsilon,\,1]$
. For $\sigma \in [\varepsilon,\,1]$![]() and $x \ge T \ge \max \{2,\,y^{1-\sigma }/\log y\}$
and $x \ge T \ge \max \{2,\,y^{1-\sigma }/\log y\}$![]() we have
we have

Corollary 3.4 rests on lemma 3.3, and makes more precise Proposition 2 of Saias [Reference Saias17].
Proof. Our starting point is the identity (1.15). (If $x \in \mathbb {Z}$![]() it still holds with an error term of $O(1)$
it still holds with an error term of $O(1)$![]() , since the integral converges to the average $(\Lambda (x+,\,y)+\Lambda (x-,\,y))/2 = \Lambda (x,\,y)+O(1)$
, since the integral converges to the average $(\Lambda (x+,\,y)+\Lambda (x-,\,y))/2 = \Lambda (x,\,y)+O(1)$![]() .) From that identity it follows that our task is equivalent to upper bounding
.) From that identity it follows that our task is equivalent to upper bounding

Recall $F(s,\,y) = \hat {\rho }((s-1)\log y)\zeta (s)(s-1)\log y$![]() . By (2.3) with $(s-1)\log y$
. By (2.3) with $(s-1)\log y$![]() instead of $s$
instead of $s$![]() we find
we find
if $y^{1-\sigma } = O(|t| \log y)$![]() , which holds by our assumptions on $T$
, which holds by our assumptions on $T$![]() . By the triangle inequality,
. By the triangle inequality,

The first integral in the right-hand side of (3.7) is estimated in lemma 3.3. To bound the second integral we apply the second moment estimate for $\zeta$![]() given in lemma 2.5. We first suppose that $\sigma \ge 1/2$
given in lemma 2.5. We first suppose that $\sigma \ge 1/2$![]() . Using Cauchy–Schwarz, the second integral in the right-hand side of (3.7) is at most
. Using Cauchy–Schwarz, the second integral in the right-hand side of (3.7) is at most

Multiplying this by the prefactor $x^{\sigma }y^{1-\sigma }/\log y$![]() , we see that this is acceptable. If $\varepsilon \le \sigma \le 1/2$
, we see that this is acceptable. If $\varepsilon \le \sigma \le 1/2$![]() we use lemma 2.3. We obtain that the second integral in the right-hand side of (3.7) is at most
we use lemma 2.3. We obtain that the second integral in the right-hand side of (3.7) is at most

concluding the proof.
Let $\alpha =\alpha (x,\,y)$![]() be the saddle point associated with $y$
be the saddle point associated with $y$![]() -smooth numbers up to $x$
-smooth numbers up to $x$![]() [Reference Hildebrand and Tenenbaum13], that is, the minimizer of the convex function $s\mapsto x^s \zeta (s,\,y)$
[Reference Hildebrand and Tenenbaum13], that is, the minimizer of the convex function $s\mapsto x^s \zeta (s,\,y)$![]() ($s>0$
($s>0$![]() ).
).
Lemma 3.5 For $\sigma \in (0,\,1]$![]() , $x\ge y \ge C$
, $x\ge y \ge C$![]() and $T \ge 2$
and $T \ge 2$![]() we have
we have
Our proof makes more precise a similar estimate appearing in Saias [Reference Saias17, p. 98], which does not allow general $y$![]() and $T$
and $T$![]() but contains the main ideas.
but contains the main ideas.
Proof. The truncated Perron's formula [Reference Hildebrand and Tenenbaum14, p. 435] bounds the error in (3.10) by

The contribution of the terms with $|\log (x/n)|\ge 1$![]() is
is

We now study the terms with $|\log (x/n)|<1$![]() . These contribute
. These contribute

The subset of terms with $|\log (x/n)| \le 1/T$![]() contributes to (3.11)
contributes to (3.11)

The contribution of the rest of the terms to (3.11), namely, those terms with $1/T<|\log (x/n)| <1$![]() , can be dyadically dissected to terms with $|\log (x/n)| \in [2^{-k},\,2^{1-k})$
, can be dyadically dissected to terms with $|\log (x/n)| \in [2^{-k},\,2^{1-k})$![]() for each integer $k\ge 1$
for each integer $k\ge 1$![]() such that $2^k<2\,T$
such that $2^k<2\,T$![]() holds. Their total contribution is
holds. Their total contribution is

where $\log _2$![]() is the base-2 logarithm. (We interpret $\Psi (a,\,y)$
is the base-2 logarithm. (We interpret $\Psi (a,\,y)$![]() for negative $a$
for negative $a$![]() as equal to $0$
as equal to $0$![]() .) Note that the sum in (3.13) dominates the right-hand side of (3.12). We shall make use of Hildebrand's inequality $\Psi (a+b,\,y)-\Psi (a,\,y) \le \Psi (b,\,y)$
.) Note that the sum in (3.13) dominates the right-hand side of (3.12). We shall make use of Hildebrand's inequality $\Psi (a+b,\,y)-\Psi (a,\,y) \le \Psi (b,\,y)$![]() , valid for $y \ge C$
, valid for $y \ge C$![]() and $a,\,b \ge y$
and $a,\,b \ge y$![]() . It implies
. It implies
for $y\ge C$![]() and all $a,\,b$
and all $a,\,b$![]() . We apply (3.14) with $a=x-Cx/2^k$
. We apply (3.14) with $a=x-Cx/2^k$![]() and $b=2Cx/2^k$
and $b=2Cx/2^k$![]() to find that (3.13) is bounded by
to find that (3.13) is bounded by

where in the second inequality we replaced $\Psi (Cx,\,y)$![]() with $\Psi (x,\,y)$
with $\Psi (x,\,y)$![]() using [Reference Hildebrand and Tenenbaum13, Thm. 3]. To conclude, we recall Theorem 2.4 of [Reference de la Bretèche and Tenenbaum5] says $\Psi (x/d,\,y) \ll \Psi (x,\,y)/d^{\alpha }$
using [Reference Hildebrand and Tenenbaum13, Thm. 3]. To conclude, we recall Theorem 2.4 of [Reference de la Bretèche and Tenenbaum5] says $\Psi (x/d,\,y) \ll \Psi (x,\,y)/d^{\alpha }$![]() holds for $x \ge y \ge 2$
holds for $x \ge y \ge 2$![]() and $1 \le d \le x$
and $1 \le d \le x$![]() . We apply this inequality with $d=2^k$
. We apply this inequality with $d=2^k$![]() and obtain
and obtain

as needed.
3.2 Proof of proposition 3.1
We first truncate the Perron integral for $\Psi (x,\,y)$![]() . We apply lemma 3.5 with $\sigma = \beta$
. We apply lemma 3.5 with $\sigma = \beta$![]() and $T=\exp ((\log y)^{4/3})$
and $T=\exp ((\log y)^{4/3})$![]() . The assumption $y \ge (\log x)^{1+\varepsilon }$
. The assumption $y \ge (\log x)^{1+\varepsilon }$![]() implies $\beta \gg _{\varepsilon } 1$
implies $\beta \gg _{\varepsilon } 1$![]() and $\Psi (x,\,y) \ge x^{c_{\varepsilon }}$
and $\Psi (x,\,y) \ge x^{c_{\varepsilon }}$![]() . Since $\alpha =\beta +O(1/\log y)$
. Since $\alpha =\beta +O(1/\log y)$![]() [Reference Hildebrand and Tenenbaum13, Lem. 2] it follows that $\alpha \gg _{\varepsilon } 1$
[Reference Hildebrand and Tenenbaum13, Lem. 2] it follows that $\alpha \gg _{\varepsilon } 1$![]() and so
and so

We use lemma 2.7 to bound the contribution of $1/\log y \le |\Im s| \le T$![]() :
:

We estimate $x^{\beta } \zeta (\beta,\,y)$![]() :
:

using (1.9) and lemma 2.2. Finally, note that both $T$![]() and $\exp (u/\log ^2(u+1))$
and $\exp (u/\log ^2(u+1))$![]() grow faster than any power of $\log x$
grow faster than any power of $\log x$![]() . We turn to $\Lambda (x,\,y)$
. We turn to $\Lambda (x,\,y)$![]() . We apply corollary 3.4 with $\sigma =\beta$
. We apply corollary 3.4 with $\sigma =\beta$![]() and
and
We obtain

We now treat the range $1/\log y\le | \Im s| \le T$![]() . By the definition of $F$
. By the definition of $F$![]() ,
,

First suppose $t \ge \pi /\log y$![]() . By the second case of lemma 2.6, this range contributes
. By the second case of lemma 2.6, this range contributes

using lemma 2.2 in the second inequality. Recall the second moment estimate for $\zeta$![]() given in lemma 2.5. It shows that right-hand side of (3.20) is bounded by
given in lemma 2.5. It shows that right-hand side of (3.20) is bounded by
where we used the functional equation if $\beta < 1/2$![]() (lemma 2.3). The contribution of $1/\log y \le t \le \pi /\log y$
(lemma 2.3). The contribution of $1/\log y \le t \le \pi /\log y$![]() to the right-hand side of (3.19) is treated using the first part of lemma 2.6, and we find that it is at most
to the right-hand side of (3.19) is treated using the first part of lemma 2.6, and we find that it is at most

using lemma 2.2 in the second inequality. In conclusion,

where

By our choice of $T$![]() and assumptions on $u$
and assumptions on $u$![]() and $y$
and $y$![]() , this can be absorbed in the error term of (3.2).
, this can be absorbed in the error term of (3.2).
3.3 Proof of proposition 3.2
We first truncate the Perron integral for $\Psi (x,\,y)$![]() . We apply lemma 3.5 with $\sigma =\beta$
. We apply lemma 3.5 with $\sigma =\beta$![]() and our $T$
and our $T$![]() , finding
, finding

In the considered range, $\Psi (x,\,y) \asymp x \rho (u)$![]() . In particular, the error term $O(1)$
. In particular, the error term $O(1)$![]() is acceptable since our $T$
is acceptable since our $T$![]() is $\ll x\rho (u) \ll \Psi (x,\,y)$
is $\ll x\rho (u) \ll \Psi (x,\,y)$![]() and so $1 \ll \Psi (x,\,y) /T^{4/5}$
and so $1 \ll \Psi (x,\,y) /T^{4/5}$![]() . Additionally, $\beta \sim 1$
. Additionally, $\beta \sim 1$![]() as $x \to \infty$
as $x \to \infty$![]() by lemma 2.1 and $\alpha =\beta +O(1/\log y)$
by lemma 2.1 and $\alpha =\beta +O(1/\log y)$![]() [Reference Hildebrand and Tenenbaum13, Lem. 2], so $\alpha \sim 1$
[Reference Hildebrand and Tenenbaum13, Lem. 2], so $\alpha \sim 1$![]() . This implies that $(\log T)/T^{\alpha } \ll 1/T^{4/5}$
. This implies that $(\log T)/T^{\alpha } \ll 1/T^{4/5}$![]() and the error term $O(\Psi (x,\,y)(\log T)/T^{\alpha })$
and the error term $O(\Psi (x,\,y)(\log T)/T^{\alpha })$![]() is also acceptable. The estimate (3.18) treats the last error term and finishes the estimation. We turn to $\Lambda (x,\,y)$
is also acceptable. The estimate (3.18) treats the last error term and finishes the estimation. We turn to $\Lambda (x,\,y)$![]() . We apply corollary 3.4 with our $T$
. We apply corollary 3.4 with our $T$![]() , obtaining
, obtaining

In our range $x\rho (u) \asymp x^{1+o(1)}$![]() , so the term $\log x$
, so the term $\log x$![]() is acceptable. We have $\exp (-u\xi ) u\log (u+1) \ll \rho (u)$
is acceptable. We have $\exp (-u\xi ) u\log (u+1) \ll \rho (u)$![]() by lemma 2.2, so the second term in the error term of (3.23) is also acceptable.
by lemma 2.2, so the second term in the error term of (3.23) is also acceptable.
4. Proofs of theorems 1.1 and 1.2
Proposition 4.1 Medium $u$
Suppose $x \ge y \ge 2$![]() satisfy
satisfy
Fix $\varepsilon >0$![]() and suppose $y \ge (\log x)^{1+\varepsilon }$
and suppose $y \ge (\log x)^{1+\varepsilon }$![]() and $x \ge C_{\varepsilon}$
and $x \ge C_{\varepsilon}$![]() . Let
. Let
Then $\Psi (x,\,y) = \Lambda (x,\,y) G(\beta,\,y) ( 1 + E)$![]() for
for

Proof. Our strategy is to establish $\Psi (x,\,y) = \Lambda (x,\,y) G(\beta,\,y) (1 + E_1 + E_2) + E_3$![]() for
for

The theorem will then follow by rearranging, once we recall that $x\rho (u) \asymp _{\varepsilon } \Lambda (x,\,y)$![]() . From proposition 3.1,
. From proposition 3.1,

which explains $E_3$![]() . Let $t_0$
. Let $t_0$![]() be as in the statement of the proposition. We upper bound the contribution of $t_0 \le |\Im s| \le 1/\log y$
be as in the statement of the proposition. We upper bound the contribution of $t_0 \le |\Im s| \le 1/\log y$![]() to the integral in the right-hand side of (4.2). We have
to the integral in the right-hand side of (4.2). We have
The triangle inequality shows, by definition of $F$![]() , that
, that

Since $-e^{-v^2/2}$![]() is the antiderivative of $e^{-v^2/2}v$
is the antiderivative of $e^{-v^2/2}v$![]() , the first part of lemma 2.6 shows
, the first part of lemma 2.6 shows

Hence, $t_0 \le |\Im s| \le 1/\log y$![]() contributes in total
contributes in total
where we used lemma 2.2 to simplify. Once we divide this by $\Lambda (x,\,y)G(\beta,\,y) \asymp _{\varepsilon } x\rho (u)G(\beta,\,y)$![]() we obtain the error term $E_2$
we obtain the error term $E_2$![]() . It remains to study the contribution of $|\Im s|\le t_0$
. It remains to study the contribution of $|\Im s|\le t_0$![]() to the integral in the right-hand side of (4.2), which will yield $E_1$
to the integral in the right-hand side of (4.2), which will yield $E_1$![]() . We Taylor-expand the integrand at $s=\beta$
. We Taylor-expand the integrand at $s=\beta$![]() . We write $s=\beta +it$
. We write $s=\beta +it$![]() , $|t|\le t_0$
, $|t|\le t_0$![]() . We first simplify the integrand using the definition of $F$
. We first simplify the integrand using the definition of $F$![]() :
:

We Taylor-expand $\log K(s-1)$![]() and $G(s,\,y)-G(\beta,\,y)$
and $G(s,\,y)-G(\beta,\,y)$![]() :
:

We expand $I(\xi -it \log y)-I(\xi )+it \log x$![]() :
:
where we used $I'(\xi (u))=u$![]() and $I^{(3)}(\xi (u)+it) \ll e^{\xi (u)}/(1+\xi (u)) \asymp u$
and $I^{(3)}(\xi (u)+it) \ll e^{\xi (u)}/(1+\xi (u)) \asymp u$![]() . This implies
. This implies

for $|t| \le t_0$![]() . By two basic properties of moments of the Gaussian,
. By two basic properties of moments of the Gaussian,

we find

By lemma 2.2, we can replace $x^{\beta } e^{I(\xi )}$![]() with $x\rho (u)\sqrt {u}$
with $x\rho (u)\sqrt {u}$![]() , to obtain
, to obtain

Dividing by $G(\beta,\,y)\Lambda (x,\,y) \asymp _{\varepsilon } G(\beta,\,y) x\rho (u)$![]() gives the error term $E_1$
gives the error term $E_1$![]() .
.
Proposition 4.2 Small $u$
Suppose $x \ge y \ge C$![]() satisfy
satisfy
Let
Then $\Psi (x,\,y) = \Lambda (x,\,y) G(\beta,\,y) ( 1 + E)$![]() for
for

Proof. Our strategy is to establish $\Psi (x,\,y) = \Lambda (x,\,y) G( \beta,\,y) (1 + E_1 + E_2 + E_3 + E_4) + E_5$![]() for
for

The proposition will then follow by rearranging and the fact that $G(\beta,\,y) \asymp 1$![]() in the considered range, unconditionally, as follows from corollary 2.9 and lemma 2.10. From proposition 3.2 with $T=t_2$
in the considered range, unconditionally, as follows from corollary 2.9 and lemma 2.10. From proposition 3.2 with $T=t_2$![]() ,
,

which explains $E_5$![]() . For $|\Im s| \le t_0$
. For $|\Im s| \le t_0$![]() , we Taylor-expand $I(\xi -it\log y)$
, we Taylor-expand $I(\xi -it\log y)$![]() as in the medium $u$
as in the medium $u$![]() range and obtain the contribution of $E_1$
range and obtain the contribution of $E_1$![]() (see (4.7)) We treat the contribution of $|\Im s| \in [t_0,\,t_1]$
(see (4.7)) We treat the contribution of $|\Im s| \in [t_0,\,t_1]$![]() . We replace $G(s,\,y)-G( \beta,\,y)$
. We replace $G(s,\,y)-G( \beta,\,y)$![]() with
with
The first two parts of lemma 2.6 show

This explains $E_2$![]() . It remains to consider $t_2 \ge |\Im s| \ge t_1$
. It remains to consider $t_2 \ge |\Im s| \ge t_1$![]() . We use the third part of lemma 2.6 to replace $\hat {\rho }((s-1)\log y)$
. We use the third part of lemma 2.6 to replace $\hat {\rho }((s-1)\log y)$![]() , appearing in $F(s,\,y)$
, appearing in $F(s,\,y)$![]() , with its approximation:
, with its approximation:

Recall $x^{ \beta } \ll x\rho (u) \sqrt {u} \exp (-I(\xi (u)))$![]() by lemma 2.2, and that $I(\xi (u)) \sim u$
by lemma 2.2, and that $I(\xi (u)) \sim u$![]() since a change of variables shows $I(r)= \mathrm {Li}(e^r)+O(\log r)\sim e^r/r$
since a change of variables shows $I(r)= \mathrm {Li}(e^r)+O(\log r)\sim e^r/r$![]() . The contribution of the error term in the right-hand side of (4.11) is
. The contribution of the error term in the right-hand side of (4.11) is

If $|t|\le 2$![]() we use $|\zeta ( \beta +it)( \beta +it-1)| \ll 1$
we use $|\zeta ( \beta +it)( \beta +it-1)| \ll 1$![]() while if $|t| \ge 2$
while if $|t| \ge 2$![]() we use lemma 2.4, to obtain an error term of size $E_3$
we use lemma 2.4, to obtain an error term of size $E_3$![]() . The main term of (4.11) gives $E_4$
. The main term of (4.11) gives $E_4$![]() .
.
4.1 Proof of theorem 1.1: medium $u$
Here we prove theorem 1.1 in the range (1.19). We obtain from proposition 4.1 that unconditionally
for
Because we assume $y \ge (\log x)^{2+\varepsilon }$![]() , we have $\beta \ge 1/2+ c_{\varepsilon }$
, we have $\beta \ge 1/2+ c_{\varepsilon }$![]() . Under RH, $\log G(\beta,\,y) = O_{\varepsilon }(1)$
. Under RH, $\log G(\beta,\,y) = O_{\varepsilon }(1)$![]() by lemma 2.11. To bound the quantities appearing in $E$
by lemma 2.11. To bound the quantities appearing in $E$![]() , we write $G(\beta +it,\,y)$
, we write $G(\beta +it,\,y)$![]() as $G_1(\beta +it,\,y)$
as $G_1(\beta +it,\,y)$![]() times $G_2(\beta +it,\,y)$
times $G_2(\beta +it,\,y)$![]() . Lemma 2.10 and equation (2.11) tell us that
. Lemma 2.10 and equation (2.11) tell us that
for $i=0,\,1,\,2$![]() and $t \in \mathbb {R}$
and $t \in \mathbb {R}$![]() . Corollary 2.9 says that under RH
. Corollary 2.9 says that under RH

for all $i=0,\,1,\,2$![]() and $|t|\le 1$
and $|t|\le 1$![]() . Putting these two together, one obtains (1.11).
. Putting these two together, one obtains (1.11).
4.2 Proof of theorem 1.1: small $u$
Here we prove theorem 1.1 for $u$![]() in the range (4.8). In this range, $\beta =1+o(1)$
in the range (4.8). In this range, $\beta =1+o(1)$![]() and $\Psi (x,\,y)=x^{1+o(1)}$
and $\Psi (x,\,y)=x^{1+o(1)}$![]() . Moreover, $\log G(\beta,\,y) = O(1)$
. Moreover, $\log G(\beta,\,y) = O(1)$![]() unconditionally by corollary 2.9 and lemma 2.10. The hardest range of the proof will be $u\asymp 1$
unconditionally by corollary 2.9 and lemma 2.10. The hardest range of the proof will be $u\asymp 1$![]() . Before proceeding with the actual proof, note that from proposition 4.2 and the triangle inequality, it follows that
. Before proceeding with the actual proof, note that from proposition 4.2 and the triangle inequality, it follows that

holds unconditionally for $t_2 \in [(\log x)^5,\, y^{4/5}]$![]() and the range $x \ge y \ge C$
and the range $x \ge y \ge C$![]() , $u \le (\log y)(\log \log y)^3$
, $u \le (\log y)(\log \log y)^3$![]() .
.
We obtain from proposition 4.2 with $t_2=y^{4/5}$![]() that
that
for $E_i$![]() bounded in (4.10). We write $G(\beta +it,\,y)$
bounded in (4.10). We write $G(\beta +it,\,y)$![]() as $G_1(\beta +it,\,y)$
as $G_1(\beta +it,\,y)$![]() times $G_2(\beta +it,\,y)$
times $G_2(\beta +it,\,y)$![]() . By lemma 2.10 and (2.11),
. By lemma 2.10 and (2.11),
for $i=0,\,1,\,2$![]() and $t \in \mathbb {R}$
and $t \in \mathbb {R}$![]() where we simplified $y^{-\beta }$
where we simplified $y^{-\beta }$![]() using (2.1). From now on we assume RH. Corollary 2.9 implies
using (2.1). From now on we assume RH. Corollary 2.9 implies
for $i=0,\,1,\,2$![]() when $|t|\le 1$
when $|t|\le 1$![]() . As in the medium $u$
. As in the medium $u$![]() case, one can bound $E_1$
case, one can bound $E_1$![]() by an acceptable quantity using our estimates for $(\log G_1)^{(i)}$
by an acceptable quantity using our estimates for $(\log G_1)^{(i)}$![]() and $(\log G_2)^{(i)}$
and $(\log G_2)^{(i)}$![]() . Recall
. Recall
where $t_1 = u\log (u+1)/\log y$![]() . If $t_1 \le 1$
. If $t_1 \le 1$![]() we bound $E_2$
we bound $E_2$![]() in the same way we bounded $E_1$
in the same way we bounded $E_1$![]() . Otherwise we use (2.8), which implies that
. Otherwise we use (2.8), which implies that
holds for $i=0,\,1,\,2$![]() and $|t|\le y^{9/10}$
and $|t|\le y^{9/10}$![]() . This shows that, if $t_1>1$
. This shows that, if $t_1>1$![]() , i.e. $u\log (u+1)\ge \log y$
, i.e. $u\log (u+1)\ge \log y$![]() ,
,
This is an acceptable contribution when $u\log (u+1)> \log y$![]() . We now study $E_3$
. We now study $E_3$![]() and $E_4$
and $E_4$![]() . Due to $G(\beta +it,\,y)/G(\beta,\,y)$
. Due to $G(\beta +it,\,y)/G(\beta,\,y)$![]() being very close to $1$
being very close to $1$![]() in our considered range by (4.17) and (4.19), we may replace
in our considered range by (4.17) and (4.19), we may replace
by
and incur a negligible error, in both $E_3$![]() and $E_4$
and $E_4$![]() . So to show $E_3$
. So to show $E_3$![]() is acceptable we need to prove
is acceptable we need to prove

This is shown using the bound
which is a consequence of (2.8) and (4.17). To handle $E_4$![]() it remains to prove
it remains to prove

Here we cannot use the triangle inequality and put absolute value inside the integral. Indeed, if we use the pointwise bound (4.21), along with our bounds for $\zeta$![]() (lemmas 2.4 and 2.5), we get a bound which falls short by a factor of $(\log y)^3$
(lemmas 2.4 and 2.5), we get a bound which falls short by a factor of $(\log y)^3$![]() . We shall overcome this by several integrations by parts as we now describe.
. We shall overcome this by several integrations by parts as we now describe.
To deal with the contribution of $\log G(\beta,\,y)$![]() to (4.22) we use (4.21) with $t=0$
to (4.22) we use (4.21) with $t=0$![]() along with the bound
along with the bound
which follows by integration by parts, where we replace $x^{it}$![]() by its antiderivative $x^{it}/\log x$
by its antiderivative $x^{it}/\log x$![]() .
.
Note that due to integration by parts, derivatives of $\zeta$![]() arise. This means that in addition to lemmas 2.4 and 2.5 we need the bounds $\zeta ^{(k)}(s) \ll _k (1+(|t|+4)^{1-\sigma })\log ^{k+1}(|t|+4)$
arise. This means that in addition to lemmas 2.4 and 2.5 we need the bounds $\zeta ^{(k)}(s) \ll _k (1+(|t|+4)^{1-\sigma })\log ^{k+1}(|t|+4)$![]() and $\int _{1}^{T} |\zeta ^{(k)}(\sigma +it)|^2 \,{\rm d}t \ll _k T$
and $\int _{1}^{T} |\zeta ^{(k)}(\sigma +it)|^2 \,{\rm d}t \ll _k T$![]() for $\sigma \in [2/3,\,1]$
for $\sigma \in [2/3,\,1]$![]() and $T,\, |t| \ge 1$
and $T,\, |t| \ge 1$![]() . These bounds follow from lemmas 2.4 and 2.5 through Cauchy's integral formula.
. These bounds follow from lemmas 2.4 and 2.5 through Cauchy's integral formula.
To deal with the contribution of $\log G(\beta +it,\,y)$![]() to (4.22) we write it $\log G_1( \beta +it,\,y)+\log G_2( \beta +it,\,y)$
to (4.22) we write it $\log G_1( \beta +it,\,y)+\log G_2( \beta +it,\,y)$![]() and obtain two integrals which we bound separately.
and obtain two integrals which we bound separately.
4.2.1 Treatment of $\log G_1$
Recall we assume $y \le x^{1-\varepsilon }$![]() . We want to show
. We want to show

We integrate by parts, replacing $x^{it}$![]() by its antiderivative, reducing matters to showing
by its antiderivative, reducing matters to showing

We divide and multiply the integrand by $y^{it}$![]() , so the left-hand side of (4.23) is now
, so the left-hand side of (4.23) is now
where $H(t):= y^{it}(G'_1/G_1)(\beta +it,\,y)$![]() . From lemma 2.8,
. From lemma 2.8,

and, for $k=1,\,2,\,3$![]() ,
,

We integrate by parts 3 times, replacing $(x/y)^{it}$![]() by its antiderivative. We are guaranteed to get enough saving since $\log (x/y) \gg _{\varepsilon } \log x$
by its antiderivative. We are guaranteed to get enough saving since $\log (x/y) \gg _{\varepsilon } \log x$![]() .
.
4.2.2 Treatment of $\log G_2$
The function $\log G_2(\beta +it,\,y)$![]() is given as a sum over proper primes powers. As the cubes and higher powers contribute at most $\ll y^{-2/3+o(1)}$
is given as a sum over proper primes powers. As the cubes and higher powers contribute at most $\ll y^{-2/3+o(1)}$![]() to it by the prime number theorem (see [Reference Gorodetsky9]), we can replace $\log G_2(\beta +it,\,y)$
to it by the prime number theorem (see [Reference Gorodetsky9]), we can replace $\log G_2(\beta +it,\,y)$![]() with the prime sum $\sum _{y^{1/2}< p \le y} p^{-2(\beta +it)}/2$
with the prime sum $\sum _{y^{1/2}< p \le y} p^{-2(\beta +it)}/2$![]() , so we are left to show
, so we are left to show

For a given $p$![]() , the pointwise bound $(x/p^2)^{it} \ll 1$
, the pointwise bound $(x/p^2)^{it} \ll 1$![]() leads to the above integral being bounded by $\ll \log y$
leads to the above integral being bounded by $\ll \log y$![]() . This is good enough for the primes $p \in [y^{1/2}\log y,\, y]$
. This is good enough for the primes $p \in [y^{1/2}\log y,\, y]$![]() , since
, since

For the primes $p \in (y^{1/2},\,y^{1/2}\log y)$![]() we integrate by parts, replacing $(x/p^2)^{it}$
we integrate by parts, replacing $(x/p^2)^{it}$![]() by its antiderivatives.
by its antiderivatives.
4.3 Proof of theorem 1.2
Suppose $(\log x)^{3} \ge y \ge (\log x)^{4/3+\varepsilon }$![]() . It follows from proposition 4.1 that $\Psi (x,\,y) = \Lambda (x,\,y) G(\beta,\,y) ( 1 + E)$
. It follows from proposition 4.1 that $\Psi (x,\,y) = \Lambda (x,\,y) G(\beta,\,y) ( 1 + E)$![]() holds unconditionally for
holds unconditionally for

where $t_0$![]() is given in the proposition. It remains to bound the quantities appearing in $E$
is given in the proposition. It remains to bound the quantities appearing in $E$![]() . From now on we assume RH. Let $A:= (\log x) / y^{1/2}$
. From now on we assume RH. Let $A:= (\log x) / y^{1/2}$![]() . We will prove the stronger bound
. We will prove the stronger bound

which implies the theorem using $\psi (y)-y \ll y^{1/2} \log ^2 y$![]() . Recall we can always simplify $y^{-\beta }$
. Recall we can always simplify $y^{-\beta }$![]() using (2.1) as $\asymp _{\varepsilon } (\log x)/y$
using (2.1) as $\asymp _{\varepsilon } (\log x)/y$![]() . In particular, $y^{1/2-\beta } \asymp _{\varepsilon } A$
. In particular, $y^{1/2-\beta } \asymp _{\varepsilon } A$![]() . Recall $G=G_1 G_2$
. Recall $G=G_1 G_2$![]() . Lemma 2.10 and equation (2.11) tell us that
. Lemma 2.10 and equation (2.11) tell us that
for $i=0,\,1,\,2$![]() and $t \in \mathbb {R}$
and $t \in \mathbb {R}$![]() . Corollary 2.9 says that under RH
. Corollary 2.9 says that under RH
for $i=0,\,1,\,2$![]() and $|t|\le 1$
and $|t|\le 1$![]() . Applying (4.28) and (4.29) with $i=1$
. Applying (4.28) and (4.29) with $i=1$![]() shows
shows
which treats the first quantity in (4.26). We now consider the third term in (4.26). Observe

From (4.28) and (4.29) we have
say, and, by (2.11) and (4.29),
so that (4.30) leads to
It remains to bound the second term in (4.26). Observe

By (2.11) we can bound the fraction in the right-hand side of (4.33) by $O_{\varepsilon }(1)$![]() :
:

The derivatives of $\log G$![]() in the right-hand side of (4.33) are handled by (4.28) and (4.29), giving
in the right-hand side of (4.33) are handled by (4.28) and (4.29), giving

Dividing this by $(\log x) (\log y)$![]() gives a bound for the second term in (4.26).
gives a bound for the second term in (4.26).
Acknowledgements
We are grateful to Sacha Mangerel for asking us about the integer analogue of [Reference Gorodetsky10]. We thank the referee for useful suggestions and comments that improved the manuscript. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement No 851318).
Appendix A. Review of $\Lambda (x,\,y)$
Appendix A.1 $\lambda _y$ and its Laplace transform
and its Laplace transform
Saias [Reference Saias17, Lem. 4(iii)] proved that $\lambda _y(v) \ll \rho (v)v^3 + e^{2v}y^{-v}$![]() holds for $y \ge 2$
holds for $y \ge 2$![]() , $v \ge 1$
, $v \ge 1$![]() . The following is a weaker version of his result which suffices for us.
. The following is a weaker version of his result which suffices for us.
Lemma A.1 Saias
If $u \ge \max \{C,\,y+1\}$![]() we have $\lambda _y(u) \ll (C/y)^{u}$
we have $\lambda _y(u) \ll (C/y)^{u}$![]() .
.
Proof. The condition $u \ge \max \{C,\,y+1\}$![]() ensures $e^{\xi (u-1)} \ge y$
ensures $e^{\xi (u-1)} \ge y$![]() :
:
Integrating the definition of $\lambda _y$![]() by parts gives
by parts gives
By (A.1) and the definition of $\rho$![]() we have
we have

One has $\rho (u-v)\ll \rho (u)e^{v \xi (u)}$![]() uniformly for $0 \le v \le u$
uniformly for $0 \le v \le u$![]() [Reference Hildebrand and Tenenbaum14, Cor. 2.4]. Hence the integral on the right-hand side of (A.2) is
[Reference Hildebrand and Tenenbaum14, Cor. 2.4]. Hence the integral on the right-hand side of (A.2) is
which is $\ll u^2 \log (u+1)$![]() by lemma 2.1. Hence
by lemma 2.1. Hence

using lemma 2.2. We have $I(\xi (u)) \ll u$![]() . As $u^{3/2}\log (u+1)$
. As $u^{3/2}\log (u+1)$![]() may be absorbed in $C^u$
may be absorbed in $C^u$![]() , we are done.
, we are done.
By lemma A.1, the contribution of $v \ge \max \{C,\,y+1\}$![]() to (1.17) is
to (1.17) is
This establishes
Corollary A.2 Fix $\varepsilon >0$![]() . If $y \ge C_{\varepsilon}$
. If $y \ge C_{\varepsilon}$![]() then $\hat {\lambda }_y$
then $\hat {\lambda }_y$![]() converges absolutely for $\Re s > -(\log y)/(1+\varepsilon )$
converges absolutely for $\Re s > -(\log y)/(1+\varepsilon )$![]() .
.
Appendix A.2 Asymptotics of $\Lambda$
We define $r \colon [1,\,\infty ) \to \mathbb {R}$![]() by $r(t):=-\rho '(t)/\rho (t)=\rho (t-1)/(t \rho (t))$
by $r(t):=-\rho '(t)/\rho (t)=\rho (t-1)/(t \rho (t))$![]() .
.
Lemma A.3 [Reference Fouvry and Tenenbaum8, Eq. (6.3)] For $0 \le v \le u-1$![]() and $u \ge 1$
and $u \ge 1$![]() we have
we have
Lemma A.4 [Reference de la Bretèche and Tenenbaum4, Lem. 3.7] For $u \ge 1$![]() we have $r(u) = \xi (u)+O(1/u)$
we have $r(u) = \xi (u)+O(1/u)$![]() .
.
Proposition A.5 Fix $\varepsilon >0$![]() . Suppose $x\ge C_{\varepsilon}$
. Suppose $x\ge C_{\varepsilon}$![]() . For $x \ge y \ge (\log x)^{1+\varepsilon }$
. For $x \ge y \ge (\log x)^{1+\varepsilon }$![]() ,
,
Equation (1.5) follows from proposition A.5 using lemma A.4. Proposition A.5, in slightly weaker form, is implicit in [Reference de la Bretèche and Tenenbaum5, pp. 176–177], and the proof given below follows these pages.
Proof. For $u=1$![]() the claim is trivial since $\Lambda (x,\,x)=\lfloor x\rfloor$
the claim is trivial since $\Lambda (x,\,x)=\lfloor x\rfloor$![]() [Reference de Bruijn3, Eq. (3.2)], so we assume $u>1$
[Reference de Bruijn3, Eq. (3.2)], so we assume $u>1$![]() . Recall the integral representation $\zeta (s)=s/(s-1) -s \int _{1}^{\infty }\{t\}\,{\rm d}t/t^{1+s}$
. Recall the integral representation $\zeta (s)=s/(s-1) -s \int _{1}^{\infty }\{t\}\,{\rm d}t/t^{1+s}$![]() for $\Re s >0$
for $\Re s >0$![]() [Reference Montgomery and Vaughan15, Eq. (1.24)]. We apply it with $s=1-r(u)/\log y$
[Reference Montgomery and Vaughan15, Eq. (1.24)]. We apply it with $s=1-r(u)/\log y$![]() and perform the change of variable $t=y^v$
and perform the change of variable $t=y^v$![]() to obtain
to obtain
From (A.3) and (A.1) we deduce
It remains to show that the right-hand side of (A.4) is
It is convenient to set
where the inequality is due to lemmas A.4 and 2.1 and our assumptions on $x$![]() and $y$
and $y$![]() . By lemma A.3, the contribution of $0 \le v \le u-1$
. By lemma A.3, the contribution of $0 \le v \le u-1$![]() to the right-hand side of (A.4) is
to the right-hand side of (A.4) is

Using $e^{(u-1)a}\gg \max \{(u-1)a,\, (u-1)^2 a^2\}$![]() and (A.5) we find that the last quantity is $\ll _{\varepsilon } x\rho (u)/((\log x)(\log y))$
and (A.5) we find that the last quantity is $\ll _{\varepsilon } x\rho (u)/((\log x)(\log y))$![]() which is acceptable. For $v > u-1$
which is acceptable. For $v > u-1$![]() , $\rho '(u-v)=0$
, $\rho '(u-v)=0$![]() and that part of the integral (times $x$
and that part of the integral (times $x$![]() ) is estimated as
) is estimated as
If $u \ge 2$![]() this is $\ll _{\varepsilon } x\rho (u) /((\log x)(\log y))$
this is $\ll _{\varepsilon } x\rho (u) /((\log x)(\log y))$![]() , otherwise this is $\ll x\rho (u)(y/x)/\log x$
, otherwise this is $\ll x\rho (u)(y/x)/\log x$![]() . Both cases give an acceptable contribution.
. Both cases give an acceptable contribution.