Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T18:03:27.642Z Has data issue: false hasContentIssue false
  • English
  • Français

Sharp estimates of semistable radial solutions of k-Hessian equations

Part of: Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  15 March 2019

Miguel Angel Navarro  and
Justino Sánchez
Miguel Angel Navarro
Affiliation:
Departamento de Estatística, Análise Matemática e Optimización Universidade de Santiago de Compostela Santiago de Compostela, 15782, Spain ([email protected])
Justino Sánchez
Affiliation:
Departamento de Matemáticas, Universidad de La Serena Avenida Cisternas 1200, La Serena, Chile ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider semistable, radially symmetric and increasing solutions of Sk(D2u) = g(u) in the unit ball of ℝn, where Sk(D2u) is the k-Hessian operator of u and g ∈ C1 is a general positive nonlinearity. We establish sharp pointwise estimates for such solutions in a proper weighted Sobolev space, which are optimal and do not depend on the specific nonlinearity g. As an application of these results, we obtain pointwise estimates for the extremal solution and its derivatives (up to order three) of the equation Sk(D2u) = λg(u), posed in B1, with Dirichlet data 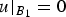$u\arrowvert _{B_1}=0$, where g is a continuous, positive, nonincreasing function such that lim t→−∞g(t)/|t|k = +∞.

Keywords

k-Hessian operatorsemistable solutionssharp estimatesextremal solution

MSC classification

Primary: 35B35: Stability
Secondary: 35B07: Axially symmetric solutions 35J60: Nonlinear elliptic equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 4 , August 2020 , pp. 2083 - 2115
Check for updates
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Cabré, X.. Regularity of minimizers of semilinear elliptic problems up to dimension 4. Comm. Pure Appl. Math. 63 (2010), 1362–1380.CrossRefGoogle Scholar
2Cabré, X. and Capella, A.. Regularity of radial minimizers and extremal solutions of semilinear elliptic equations. J. Funct. Anal. 238 (2006), 709–733.CrossRefGoogle Scholar
3Cabré, X., Capella, A. and Sanchón, M.. Regularity of radial minimizers of reaction equations involving the p-Laplacian. Calc. Var. Partial Diff. Equ. 34 (2009), 475–494.CrossRefGoogle Scholar
4Caffarelli, L., Nirenberg, L. and Spruck, J.. The Dirichlet problem for nonlinear second-order elliptic equations. III. Functions of the eigenvalues of the Hessian. Acta Math. 155 (1985), 261–301.CrossRefGoogle Scholar
5Chou, K.-S. and Wang, X.-J.. A variational theory of the Hessian equation. Comm. Pure Appl. Math. 54 (2001), 1029–1064.CrossRefGoogle Scholar
6Jacobsen: Global bifurcation problems associated with k-hessian operators. Topol. Meth. Nonlinear Anal. 14 (1999), 81–130.CrossRefGoogle Scholar
7Jacobsen, J.. A Liouville-Gelfand equation for k-Hessian operators. Rocky Mountain J. Math. 34 (2004), 665–683.CrossRefGoogle Scholar
8Jacobsen, J. and Schmitt, K.. The Liouville-Bratu-Gelfand problem for radial operators. J. Diff. Equ. 184 (2002), 283–298.CrossRefGoogle Scholar
9Joseph, D. D. and Lundgren, T. S.. Quasilinear Dirichlet problems driven by positive sources. Arch. Rational Mech. Anal. 49 (1972/73), 241–269.CrossRefGoogle Scholar
10Lieberman, G. M.. Boundary regularity for solutions of degenerate elliptic equations. Nonlinear Anal. 12 (1988), 1203–1219.CrossRefGoogle Scholar
11Mignot, F. and Puel, J.-P.. Sur une classe de problèmes non linéaires avec non linéairité positive, croissante, convexe. Comm. Partial Diff. Equ. 5 (1980), 791–836.CrossRefGoogle Scholar
12Navarro, M. and Villegas, S.. The sharpness of some results on stable solutions of − Δu = f(u) in ℝN. J. Math. Anal. Appl. 397 (2013), 693–696.CrossRefGoogle Scholar
13Navarro, M. and Villegas, S.. Sharp estimates of radial minimizers of p-Laplace equations. Proc. Amer. Math. Soc. 145 (2017), 2931–2941.CrossRefGoogle Scholar
14Nedev, G.. Regularity of the extremal solution of semilinear elliptic equations. C. R. Acad. Sci. Paris Sér. I Math. 330 (2000), 997–1002.CrossRefGoogle Scholar
15Sánchez, J. and Vergara, V.. Bounded solutions of a k-Hessian equation in a ball. J. Diff. Equ. 261 (2016), 797–820.CrossRefGoogle Scholar
16Trudinger, N. S. and Wang, X.-J.. Hessian measures. I. Topol. Meth. Nonlinear Anal. 10 (1997), 225–239. Dedicated to Olga Ladyzhenskaya.CrossRefGoogle Scholar
17Trudinger, N. S. and Wang, X.-J.. Hessian measures. II. Ann. of Math. (2) 150 (1999), 579–604.CrossRefGoogle Scholar
18Tso: On symmetrization and hessian equations. J. Analyse Math. 52 (1989), 94–106.Google Scholar
19Tso, K.. Remarks on critical exponents for Hessian operators. Ann. Inst. H. Poincaré Anal. Non Linéaire 7 (1990), 113–122.CrossRefGoogle Scholar
20Verbitsky, I. E.. The Hessian Sobolev inequality and its extensions. Discrete Contin. Dyn. Syst. 35 (2015), 6165–6179.CrossRefGoogle Scholar
21Villegas, S.. Sharp estimates for semi-stable radial solutions of semilinear elliptic equations. J. Funct. Anal. 262 (2012), 3394–3408.CrossRefGoogle Scholar
22Villegas: Boundedness of extremal solutions in dimension 4. Adv. Math. 235 (2013), 126–133.CrossRefGoogle Scholar
23Wang, X.-J.. A class of fully nonlinear elliptic equations and related functionals. Indiana Univ. Math. J. 43 (1994), 25–54.CrossRefGoogle Scholar
24Wang, X.-J.. The k-Hessian equation. In Geometric analysis and PDEs. Lectures from the C.I.M.E. Summer School held in Cetraro, June 11–16, 2007 (eds. Ambrosetti, A., Chang, S.-Y. A. and Malchiodi, A.). Volume 1977 of Lecture Notes in Mathematics, pp. 177–252 (Dordrecht: Springer; Florence: Fondazione C.I.M.E., 2009).Google Scholar