Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-20T08:13:44.593Z Has data issue: false hasContentIssue false
  • English
  • Français

Sharp convergence for sequences of Schrödinger means and related generalizations

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  25 September 2023

Wenjuan Li ,
Huiju Wang  and
Dunyan Yan
Wenjuan Li
Affiliation:
School of Mathematics and Statistics, Northwestern Polytechnical University, Xi'an 710129, China ([email protected])
Huiju Wang
Affiliation:
School of Mathematics and Statistics, Henan University, Kaifeng 475000, China ([email protected])
Dunyan Yan
Affiliation:
School of Mathematics Sciences, University of Chinese Academy of Sciences, Beijing 100049, China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

For decreasing sequences $\{t_{n}\}_{n=1}^{\infty }$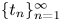 converging to zero and initial data $f\in H^s(\mathbb {R}^N)$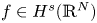, $N\geq 2$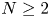, we consider the almost everywhere convergence problem for sequences of Schrödinger means ${\rm e}^{it_{n}\Delta }f$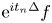, which was proposed by Sjölin, and was open until recently. In this paper, we prove that if $\{t_n\}_{n=1}^{\infty }$ 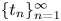belongs to Lorentz space ${\ell }^{r,\infty }(\mathbb {N})$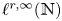, then the a.e. convergence results hold for $s>\min \{\frac {r}{\frac {N+1}{N}r+1},\,\frac {N}{2(N+1)}\}$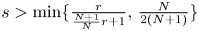. Inspired by the work of Lucà-Rogers, we construct a counterexample to show that our a.e. convergence results are sharp (up to endpoints). Our results imply that when $0< r<\frac {N}{N+1}$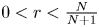, there is a gain over the a.e. convergence result from Du-Guth-Li and Du-Zhang, but not when $r\geq \frac {N}{N+1}$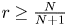, even though we are in the discrete case. Our approach can also be applied to get the a.e. convergence results for the fractional Schrödinger means and nonelliptic Schrödinger means.

Keywords

Schrödinger meanalmost everywhere convergencemaximal functionspointwise convergence

MSC classification

Primary: 42B25: Maximal functions, Littlewood-Paley theory
Secondary: 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 17
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barceló, J. A., Bennett, J. M., Carbery, A., Ruiz, A. and Vilela, M. C.. Some special solutions of the Schrödinger equation. Indiana Univ. Math. J. (2007), 1581–1593.CrossRefGoogle Scholar
Bourgain, J.. A note on the Schrödinger maximal function. J. Anal. Math. 130 (2016), 393–396.CrossRefGoogle Scholar
Carleson, L., Some analytic problems related to statistical mechanics. Euclidean harmonic analysis. (Springer, Berlin, Heidelberg, 1980), pp. 5–45.CrossRefGoogle Scholar
Cho, C. and Ko, H., Note on maximal estimates of generalized Schrödinger equation. preprint arXiv:1809.03246v2 (2019).Google Scholar
Cho, C., Ko, H., Koh, Y. and Lee, S.. Pointwise convergence of sequential Schrödinger means. J. Inequal. Appl. 2023 (2023), 54. doi: 10.1186/s13660-023-02964-8.CrossRefGoogle Scholar
Dahlberg, B. E. J. and Kenig, C. E., A note on the almost everywhere behavior of solutions to the Schrödinger equation, in Harmonic Analysis (Minneapolis, Minn., 1981), Lecture Notes in Math. Vol. 908 (Springer-Verlag, New York, 1982), pp. 205–209.CrossRefGoogle Scholar
Dimou, E. and Seeger, A.. On pointwise convergence of Schrödinger means. Mathematika 66 (2020), 356–372.CrossRefGoogle Scholar
Du, X., Guth, L. and Li, X.. A sharp Schrödinger maximal estimate in $\mathbb {R}^2$. Ann. Math. 186 (2017), 607–640.CrossRefGoogle Scholar
Du, X. and Zhang, R.. Sharp $L^2$ estimates of the Schrödinger maximal function in higher dimensions. Ann. Math. 189 (2019), 837–861.CrossRefGoogle Scholar
Kenig, E. C., Ponce, G. and Vega, L.. Oscillatory integrals and regularity of dispersive equations. Indiana Univ. Math. J. 40 (1991), 33–69.CrossRefGoogle Scholar
Lee, S. and Rogers, K. M.. The Schrödinger equation along curves and the quantum harmonic oscillator. Adv. Math. 229 (2012), 1359–1379.CrossRefGoogle Scholar
Lucà, R. and Rogers, K.. A note on pointwise convergence for the Schrödinger equation. Math. Proc. Camb. Philos. Soc. 166 (2019), 209–218.CrossRefGoogle Scholar
Rogers, M. K., Vargas, A. and Vega, L.. Pointwise convergence of solutions to the nonelliptic Schrödinger equation. Indiana Univ. Math. J. (2006), 1893–1906.CrossRefGoogle Scholar
Sjölin, P.. Two theorems on convergence of Schrödinger means. J. Fourier Anal. Appl. 25 (2019), 1708–1716.CrossRefGoogle Scholar
Sjölin, P. and Strömberg, J.. Convergence of sequences of Schrödinger means. J. Math. Anal. Appl. 483 (2020), 123580.CrossRefGoogle Scholar
Walther, B. G.. Higher integrability for maximal oscillatory Fourier integrals. Ann. Acad. Sci. Fenn. Ser. A. I. Math. 26 (2001), 189–204.Google Scholar