Sharp conditions for the validity of the Bourgain–Brezis–Mironescu formula

Abstract

Following the seminal paper by Bourgain, Brezis, and Mironescu, we focus on the asymptotic behaviour of some nonlocal functionals that, for each $u\in L^2(\mathbb {R}^N)$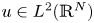, are defined as the double integrals of weighted, squared difference quotients of $u$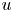. Given a family of weights $\{\rho _{\varepsilon} \}$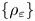, $\varepsilon \in (0,\,1)$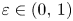, we devise sufficient and necessary conditions on $\{\rho _{\varepsilon} \}$ 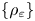for the associated nonlocal functionals to converge as $\varepsilon \to 0$ 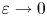to a variant of the Dirichlet integral. Finally, some comparison between our result and the existing literature is provided.

1. Introduction

Let $J := (0,\, 1)$ and let $u\colon \mathbb {R}^N \to \mathbb {R}$ be an $L^2$ function. Given the family of kernels $\{\rho _{\varepsilon} \}_{\varepsilon \in J}$, with $\rho _{\varepsilon} \colon \mathbb {R}^N \to [0,\,+\infty )$ measurable, we consider the energy functionals:

(1.1)\begin{equation} \mathscr{F}_{\varepsilon} [ u ] := \frac{1}{2}\int_{\mathbb{R}^N \times \mathbb{R}^N} \rho_{\varepsilon} (y-x) \frac{| u (y) - u (x) |^2}{| y - x |^2} \,\mathrm{d} y \,\mathrm{d} x. \end{equation}

We aim to characterize the class of kernels such that for every $u\in H^1(\mathbb {R}^N)$ the family $\{\mathscr {F}_{\varepsilon} [ u ]\}$ converges to (a variant of) $\| \nabla u \|^2_{L^2(\mathbb {R}^N)}$ as $\varepsilon \to 0$, see theorem 1.1.

Our study follows the line of research initiated in the renowned paper [5]. The motivation advanced by the authors was the analysis of the Gagliardo seminorms:

\[ [u]^p_s := \int_{\mathbb{R}^N \times \mathbb{R}^N} \frac{| u (y) - u (x) |^{p}}{| y - x |^{N+sp}} \,\mathrm{d} y \,\mathrm{d} x, \quad \text{with}\ p\in(1,+\infty),s\in(0,1) \]

as $s\to 1$. They studied the asymptotics as $\varepsilon \to 0$ of double integrals with the same structure as the one in (1.1) for a family $\{\rho _{\varepsilon} \}\subset L^1(\mathbb {R}^N)$ of radial kernels and a general exponent $p\in (1,\,+\infty )$, and they proved that the Sobolev seminorm $\|\nabla u\|^p_{L^p(\mathbb {R}^N)}$ is retrieved in the limit. The case of the Gagliardo seminorms may be treated analogously upon taking some extra care of the tails of the fractional kernel (see, e.g. [13, Sec. 1]).

The literature on nonlocal-to-local formulas has become extremely vast, and a detailed overview is beyond the scope of our contribution. Here, we restrict ourselves to the research that is most close in spirit to [5]. The gap left open for the case $p=1$ was filled in [9], where a characterization of functions of bounded variation was provided (see also [13, 19]). The case of vector fields of bounded deformations was later addressed in [15] by considering a suitable symmetrization of the functionals in (1.1) (see also [16] for the asymptotics of nonlocal elastic energies of peridynamic-type and [21] for a study of fractional Korn inequalities). The analysis of the asymptotic behaviour in the sense of $\Gamma$-convergence [8] of the fractional perimeter functionals introduced in [7] was undertaken in [2], and then extended in multiple directions by several contributions, e.g. [4, 10, 14, 17]. Finally, we point out that a general variational framework for the analysis of (static and dynamic) multiscale problems that feature nonlocal interactions has been very recently considered in the monograph [1], again for kernels that, in our notation, are required to form a definitively bounded sequence in $L^1$.

A common trait of the works above is that they only concern sufficient conditions for the nonlocal-to-local formulas to hold. In the specific case of the functionals in (1.1) (see theorem 5.4 for a prototypical statement), this means that, given a measurable map $\rho _{\varepsilon} \colon \mathbb {R}^N \to [0,\,+\infty )$ for every $\varepsilon \in J$, a set of conditions on the family $\{\rho _{\varepsilon} \}_{\varepsilon \in J}$ is prescribed, so that the following can be deduced: there exist an infinitesimal sequence $\{\varepsilon _k\}\subset J$ and a positive Radon measure $\lambda$ on the unit sphere $\mathbb {S}^{N-1}$ that depends only on $\{\rho _{\varepsilon _k}\}_{\varepsilon _k\in J}$, such that for every $u\in H^1(\mathbb {R}^N)$:

(1.2)\begin{equation} \lim_{k\to+\infty} \mathscr{F}_{\varepsilon_k}[u] = \int_{\mathbb{R}^N} \int_{\mathbb{S}^{N-1}} | \nabla u(x) \cdot \sigma |^2 \,\mathrm{d} \lambda(\sigma) \,\mathrm{d} x. \end{equation}

We refer to such equality as the Bourgain–Brezis–Mironescu formula, in short BBM formula. The novelty of our contribution is that we devise conditions that are both necessary and sufficient for (1.2) to hold (see also § 5.3 for some remarks about energies with non-quadratic growth). Precisely, we establish the following.

Theorem 1.1 (Necessary conditions for the BBM formula)

For every $\varepsilon \in J$, let $\rho _{\varepsilon} \colon \mathbb {R}^N \to [0,\,+\infty )$ be measurable and let $\mathscr {F}_{\varepsilon}$ be as in (1.1). Let also $\lambda$ be a fixed positive Radon measure on the unit sphere $\mathbb {S}^{N-1}$.

Suppose that there exists an infinitesimal sequence $\{\varepsilon _k\}\subset J$ such that for every $u\in H^1(\mathbb {R}^N)$ the BBM formula (1.2) holds for the given measure $\lambda$. Then, the sequence $\{\rho _{\varepsilon _k}\}$ satisfies the following:

1. (i) there exists $M\geq 0$ with the property that for every $R>0$:

   (1.3)\begin{equation} \limsup_{k\to+\infty}\left[ \int_{B(0,R)} \rho_{\varepsilon_k}(z)\,\mathrm{d} z + R^2 \int_{B(0,R)^c} \frac{\rho_{\varepsilon_k}( z)}{| z |^2} \,\mathrm{d} z \right] \leq M; \end{equation}

2. (ii) the sequence $\{\nu _k\}$ of Radon measures on $\mathbb {R}^N$ defined by

   (1.4)\begin{equation} \langle \nu_k , f \rangle := \int_{\mathbb{R}^N} \rho_{\varepsilon_k}(z) f(z) \,\mathrm{d} z \quad\text{for all}\ f\in C_c(\mathbb{R}^N), \end{equation}
   locally weakly-$\ast$ converges in the sense of Radon measures to $\alpha \delta _0$, where $\alpha \geq 0$ is a positive constant, and $\delta _0$ is the Dirac delta in $0$.

Roughly speaking, condition (i) prescribes that for $\varepsilon \in J$ small enough each kernel $\rho _{\varepsilon}$ must have finite mass in any large ball around the origin, and that, at the same time, the contributions accounting for long-range interactions must be asymptotically negligible. Indeed, as we show in § 5.1, (1.3) is equivalent to the following uniform decay condition: there exists $M\geq 0$ such that for every $R>0$:

\[ \limsup_{k\to +\infty}\int_{\mathbb{R}^N}\frac{\rho_{\varepsilon_k}(z)}{R^2+|z|^2}\,\mathrm{d} z \leq \frac{M}{R^2}. \]

When $R=1$, the previous inequality entails that for $k$ large enough $\rho _{\varepsilon _k}\in L^1_{\rm loc}(\mathbb {R}^N)$, so that, in particular, position (1.4) actually defines a Radon measure on $\mathbb {R}^N$. A useful way to regard the measures $\nu _k$ in (1.4) is to think of them as quantities encoding medium-range interactions, although this is not immediately evident from the definition. From this point of view, condition (ii) shows us that, in the limit, such interactions must vanish outside of the origin. We will elaborate further on this point in this introduction.

It turns out that conditions (i) and (ii) are also sufficient for the BBM formula to hold, so that, in light of theorem 1.1, they are sharp. To establish the sufficiency, we need the following compactness result, which is interesting on its own:

Theorem 1.2 (Asymptotic behaviour of nonlocal energies)

For every $\varepsilon \in J$, let $\rho _{\varepsilon} \colon \mathbb {R}^N \to [0,\,+\infty )$ be measurable and let $\mathscr {F}_{\varepsilon}$ be as in (1.1).

Suppose that there exists $M\geq 0$ with the property that for every $R>0$:

(1.5)\begin{equation} \limsup_{\varepsilon\to 0} \left[ \int_{B(0,R)} \rho_{\varepsilon}(z)\,\mathrm{d} z + R^2 \int_{B(0,R)^c} \frac{\rho_{\varepsilon}( z)}{| z |^2} \,\mathrm{d} z \right] \leq M. \end{equation}

Then, there exist an infinitesimal sequence $\{\varepsilon _k\}\subset J$ and two finite positive Radon measures $\mu$ and $\nu$, respectively on $\mathbb {S}^{N-1}$ and $\mathbb {R}^N$, that depend only on $\{\rho _{\varepsilon _k}\}$, and such that for every $u\in H^1(\mathbb {R}^N)$ there holds:

(1.6)\begin{align} \lim_{k\to+\infty} \mathscr{F}_{\varepsilon_k}[u] & = \frac{1}{2}\int_{\mathbb{R}^N} \left[ \vphantom{\frac{\rho_{\varepsilon}( z)}{| z |^2}} \int_{\mathbb{S}^{N-1}} | \nabla u(x) \cdot \sigma |^2 \,\mathrm{d} \mu(\sigma)\right.\notag\\ & \quad + \left. \int_{\mathbb{R}^N\setminus\{0\}} \frac{| u (x+z) - u (x) |^2}{| z |^2} \,\mathrm{d} \nu(z) \right] \mathrm{d} x. \end{align}

Moreover, the right-hand side of (1.6) is finite for every $u\in H^1(\mathbb {R}^N)$.

Theorem 1.2 shows that, while the integrability and decay conditions in (i) are sufficient to establish the convergence of the functionals in (1.1), in the absence of condition (ii) we cannot exclude the persistence of nonlocal terms in the limit. Indeed, the measure $\nu$ is retrieved as the limit (in the sense of weak-$\ast$ convergence) of the medium-range interactions encoded by (1.4). The measure $\mu$ captures instead the concentration of the sequence $\{\rho _{\varepsilon _k}\}$ around the origin, and it characterizes the (possibly zero) local term in the limiting energy. Loosely speaking, for every Borel subset $E\subseteq \mathbb {S}^{N-1}$, $\mu$ is given by

\[ \mu(E):= \lim_{\delta\to 0}\int_{C_\delta(E)}\rho_{\varepsilon_\delta}(z) \,\mathrm{d} z \]

where $C_\delta (E)$ is the intersection of the cone spanned by $E$ with $B(0,\,\delta )$, $\{\varepsilon _\delta \}$ is a suitable subfamily, and the limit is taken in the sense of the weak-$\ast$ convergence of measures. We refer to steps 3 and 4 in the proof of proposition 3.2 for the precise definition. In particular, when the kernels $\rho _{\varepsilon _k}$ are radial (cf. [5]), then $\mu =c\mathscr {H}^{N-1}\lfloor {\mathbb {S}^{N-1}}$ for a constant $c\geq 0$.

We conclude our analysis by showing that, when (ii) is imposed as well, the limiting nonlocal effects vanish.

Corollary 1.3 (Sharp sufficient conditions for the BBM formula)

Let us suppose that same hypotheses of theorem 1.2 hold, and let us suppose also that the family $\{\nu _{\varepsilon} \}_{\varepsilon \in J}$ of Radon measures on $\mathbb {R}^N$ defined by

(1.7)\begin{equation} \langle \nu_{\varepsilon} , f \rangle := \int_{\mathbb{R}^N} \rho_{\varepsilon}(z) f(z) \,\mathrm{d} z \quad\text{for all}\ f\in C_c(\mathbb{R}^N), \end{equation}

locally weakly-$\ast$ converges in the sense of Radon measures to $\alpha \delta _0$, where $\alpha \geq 0$ is a positive constant, and $\delta _0$ is the Dirac delta in $0$. Then, there exist an infinitesimal sequence $\{\varepsilon _k\}\subset J$ and a finite positive Radon measure $\mu$ on $\mathbb {S}^{N-1}$ such that the BBM formula holds, that is,

(1.8)\begin{equation} \lim_{k\to+\infty} \mathscr{F}_{\varepsilon_k}[u] = \frac{1}{2} \int_{\mathbb{R}^N}\int_{\mathbb{S}^{N-1}} | \nabla u(x) \cdot \sigma |^2 \,\mathrm{d} \mu(\sigma) \,\mathrm{d} x. \end{equation}

We refer to remark 4.3 for an alternative formulation of the right-hand side of (1.8) in terms of the action of a quadratic form.

Our approach grounds on the use of the Fourier transform, which allows recasting the family of nonlocal functionals in (1.1) into double integrals of the form:

(1.9)\begin{equation} \int_{\mathbb{R}^N} | \psi (\xi) |^2 \int_{\mathbb{R}^N} \rho_{\varepsilon}( z)\frac{1 - \cos( z\cdot \xi )}{| z |^2} \,\mathrm{d} z \,\mathrm{d} \xi, \end{equation}

with $\psi$ in a suitable weighted $L^2$ space (see (2.1) and (2.3)). The technical preliminaries about the Fourier transform and those on Radon measures to be used later in this work are collected in § 2. In particular, the functionals in (1.9) and equivalent formulations of the BBM formula in Fourier variables are retrieved in lemma 2.1.

From § 3, we turn to the proof of our results. First, we establish theorem 1.2 by observing that the condition in (1.5) grants not only that the integrals with respect to $z$ in (1.9), as a function of $\xi$, grow at most as $1+|\xi |^2$ (see lemma 3.1), but also that they converge pointwise to the Fourier transform of the integrals within the square brackets in (1.6) (see proposition 3.2). The dominated convergence theorem then applies, and (1.6) is retrieved.

The pointwise convergence of the nonlocal energies provided by proposition 3.2 plays a central role in our analysis. It is obtained by studying separately the behaviours of the family $\{\rho _{\varepsilon} \}$ at three distinct interaction ranges, respectively short, medium and long, that we encode by means of an additional parameter $\delta \in J$. Short-range interactions arise from the contributions of shrinking balls of radius $\delta$ centred in the origin, and, as $\delta \to 0$, they asymptotically approach the gradient term in (1.6). Medium-range interactions originate from the contributions to the energy stored in annuli that lie at a distance $\delta$ from the origin. In the limit, their presence leads to the nonlocal term in (1.6), that is, the integral with respect to the measure $\nu$. Finally, long-range interactions occur outside of balls of radius $\delta ^{-1}$ centred in the origin, and their contributions are negligible when $\delta \to 0$.

The proofs of our two other results are provided in § 4. With theorem 1.2 on hand, corollary 1.3, that is, the sufficiency of conditions (i) and (ii) in theorem 1.1 for the BBM formula, follows quickly: it is enough to observe that (ii) forces the integral with respect to $\nu$ in (1.6) to vanish. In this sense, (ii) may be regarded as a locality condition, since it requires that in the limit the kernels concentrate at the origin. Conditions of this sort appear to be natural as far as sufficient criteria for the convergence of the nonlocal energies to variants of the Dirichlet norm are sought after (cf., e.g. (5.4) in theorem 5.4 or [1, Thm. 3.1]). The key novelty of our contribution is that we prove item (ii) in theorem 1.1 to be the weakest locality requirement for the BBM formula (1.2) to hold.

Proving theorem 1.1, that is, the necessity of (i) and (ii) for the validity of the BBM formula, is a more delicate issue. The key step is established in proposition 4.1, where, by a suitable scaling of the functions in (1.9) (see remark 4.2), it is proved that (5.5) implies (i). The weak-$\ast$ convergence of the sequence $\{\nu _k\}$ in (ii) to a multiple of the Dirac delta in $0$ follows then from a homogeneity argument. We conclude our contribution in § 5 by clarifying how it compares with the existing literature and by pointing out possible future research directions.

As we briefly outlined above, there have been intense research efforts in the asymptotic analysis of nonlocal energies of the form (1.1). It is to be noted that such functionals also arise in applications, a case of interest being represented, for instance, by nonlocal models in micromagnetics. Indeed, as pointed out in [20], if the classical symmetric exchange energy given by the Dirichlet integral of the magnetization is replaced by a nonlocal Heisenberg functional of the form (1.1), then a model closer to atomistic theories is obtained, and, in addition, the class of admissible magnetizations may be enlarged to include discontinuous and even ‘measure-valued’ fields. This observation is crucial in nonconvex problems such as those of ferromagnetism, in which the highly oscillatory ‘domain structures’ observed in ferromagnetic materials cannot be captured by magnetizations with Sobolev regularity. In such nonlocal micromagnetics models, knowing what classes of kernels $\rho _{\varepsilon}$ lead to an approximation of the classical Dirichlet energies amounts to a selection criterion to establish whether nonlocal descriptions can be replaced by local ones or, instead, such approximations are not mathematically correct. We refer to [11] for further discussion on this topic.

2. Preliminaries

After fixing the notation, in this section, we provide a concise overview of some facts from the theories of the Fourier transform and of Radon measures, which will serve as the main tools for our study. In particular, in lemma 2.1 we derive an equivalent form of the BBM formula (1.2) to be employed as the cornerstone of our analysis.

For $N\in \mathbb {N}\setminus \{0\}$, we work in the $N$-dimensional Euclidean space $\mathbb {R}^N$, endowed with the corresponding inner product $\,\cdot \,$ and norm $|\,|$. We let $\{e_1,\,\dots,\,e_N\}$ be its canonical basis. For all $z\in \mathbb {R}^N\setminus \{0\}$ we define $\widehat z := z / | z |$. We denote by $\mathscr {L}^N$ and $\mathscr {H}^{N-1}$ the $N$-dimensional Lebesgue and the $(N-1)$-dimensional Hausdorff measures, respectively. We let $B(x,\,r)$ be the open ball in $\mathbb {R}^N$ of centre $x$ and radius $r$. We write $B(x,\,r)^c$ for the complement of $B(x,\,r)$, while the topological boundary of $B(0,\,1)$ is denoted by $\mathbb {S}^{N-1}$.

2.1. Fourier transform

In this paper, we resort to results on the Fourier transform that are standard and can be found in any textbook on Fourier analysis (see, e.g. [22]). Here, we briefly recall the properties to be used below.

We will employ the unitary Fourier transform expressed in terms of angular frequency, that is, for any rapidly decaying $u\in C^\infty (\mathbb {R}^N)$ and $\xi \in \mathbb {R}^N$:

\[ \mathcal{F}u(\xi):= \frac{1}{(2\pi)^{N/2}} \int_{\mathbb{R}^N}\,{\rm e}^{-{\rm i} x\cdot \xi} u(x)\,\mathrm{d} x. \]

As customary, we will adopt $\widehat {u}$ as a shorthand for $\mathcal {F}u$. We recall that the following identities hold:

\[ \widehat{\tau_z u}(\xi)={\rm e}^{-{\rm i}z\cdot \xi} \widehat{u}(\xi), \quad \widehat{\partial_\alpha u}(\xi)=({\rm i} \xi )^\alpha \widehat{u}(\xi), \]

where $( \tau _z u ) (x) := u(x - z)$, for $x,\,z,\,\xi \in \mathbb {R}^N$, and where $\alpha \in \mathbb {N}^N$ is a multi-index. In particular, we observe that, by the Parseval identity, the Fourier transform is a bijection between

\[ H^1(\mathbb{R}^N):= \left\{ u\in L^2(\mathbb{R}^N) : \text{the distribution}\ \nabla u\ \text{is in}\ L^2(\mathbb{R}^N)\right\} \]

and the weighted space

(2.1)\begin{equation} L^2_w(\mathbb{R}^N) := \left\{ \psi\in L^2(\mathbb{R}^N) : \int_{\mathbb{R}^N} |\xi|^2|\psi(\xi)|^2\,\mathrm{d} \xi <{+}\infty \right\}. \end{equation}

By applying Fourier techniques to the functionals in (1.2), the following is readily obtained.

Lemma 2.1 Let $\lambda$ be a positive Radon measure on $\mathbb {S}^{N-1}$. For every $u \in H^1 ( \mathbb {R}^N )$ we define

(2.2)\begin{equation} \mathscr{F}[u]:= \int_{\mathbb{R}^N} \int_{\mathbb{S}^{N-1}} | \nabla u(x) \cdot \sigma |^2 \,\mathrm{d} \lambda(\sigma) \,\mathrm{d} x, \end{equation}

while for every $\psi \in L^2_w(\mathbb {R}^N)$ we set

(2.3)\begin{align} \widehat{\mathscr{F}}_{\varepsilon}[\psi]& := \int_{\mathbb{R}^N} | \psi (\xi) |^2 \int_{\mathbb{R}^N} \rho_{\varepsilon}( z)\frac{1 - \cos( z\cdot \xi )}{| z |^2} \,\mathrm{d} z \,\mathrm{d} \xi, \end{align}

(2.4)\begin{align} \widehat{\mathscr{F}}[\psi]& := \int_{\mathbb{R}^N} |\psi (\xi) |^2 \int_{\mathbb{S}^{N-1}} | \xi \cdot \sigma |^2 \,\mathrm{d} \lambda(\sigma) \,\mathrm{d} \xi. \end{align}

Then, recalling (1.1), for every $u \in H^1 ( \mathbb {R}^N )$ it holds

\[ \mathscr{F}_{\varepsilon}[u]=\widehat{\mathscr{F}}_{\varepsilon}[\widehat u], \quad \mathscr{F}[u]=\widehat{\mathscr{F}}[\widehat u], \]

and, in particular, there exist an infinitesimal sequence $\{\varepsilon _k\}\subset J$ such that (1.2) holds for every $u\in H^1(\mathbb {R}^N)$ if and only if for every $\psi \in L^2_w(\mathbb {R}^N)$

(2.5)\begin{equation} \lim_{k\to+\infty}\widehat{\mathscr{F}}_{\varepsilon_k}[\psi]=\widehat{\mathscr{F}}[\psi]. \end{equation}

Proof. Recall that $( \tau _z u ) (x) := u(x - z)$ for every $x,\,z\in \mathbb {R}^N$. By the change of variables $z := y - x$ and the Parseval identity we obtain:

\begin{align*} \mathscr{F}_{\varepsilon} [ u ] & = \frac{1}{2} \int_{\mathbb{R}^N \times \mathbb{R}^N} \frac{\rho_{\varepsilon}(z)}{| z |^2} | u (x + z) - u (x) |^2 \,\mathrm{d} z \,\mathrm{d} x \\ & = \frac{1}{2} \int_{\mathbb{R}^N} \frac{\rho_{\varepsilon}(z)}{| z |^2} \int_{\mathbb{R}^N} | \tau_{- z} u (x) - u (x) |^2 \,\mathrm{d} x \,\mathrm{d} z \\ & = \frac{1}{2} \int_{\mathbb{R}^N} \frac{\rho_{\varepsilon}( z)}{| z |^2} \int_{\mathbb{R}^N} | \mathcal{F} [ u - \tau_{- z}u ] (\xi) |^2 \,\mathrm{d} \xi \,\mathrm{d} z. \end{align*}

The properties of the Fourier transform yield:

\[ | \mathcal{F} [ u - \tau_{- z}u ] (\xi) |^2 = | 1 - {\rm e}^{{\rm i} z\cdot \xi} |^2 | \widehat{u} (\xi) |^2 = 2 \left( 1 - \cos( z\cdot \xi ) \right) | \widehat{u} (\xi) |^2, \]

whence we infer $\mathscr {F}_{\varepsilon} [u]=\widehat{\mathscr{F}}_{\varepsilon} [\widehat u]$. Similarly, we have

\begin{align*} \mathscr{F}[u] & = \int_{\mathbb{S}^{N-1}} \int_{\mathbb{R}^N} | \mathcal{F}[\nabla u \cdot \sigma](\xi) |^2 \,\mathrm{d} \xi \,\mathrm{d} \lambda(\sigma) \\ & = \int_{\mathbb{R}^N} |\widehat{u} (\xi) |^2 \int_{\mathbb{S}^{N-1}} | \xi \cdot \sigma |^2 \,\mathrm{d} \lambda(\sigma) \,\mathrm{d} \xi \\ & = \widehat{\mathscr{F}}[\widehat u]. \end{align*}

We then achieve the conclusion thanks to the one-to-one correspondence between $H^1(\mathbb {R}^N)$ and $L^2_w(\mathbb {R}^N)$ provided by the Fourier transform.

2.2. Positive Radon measures on $\mathbb {R}^N$

We recall here some definitions and properties that may be found, e.g. in [3, Secs. 1.3 and 1.4]; we refer to such a monograph for a more detailed study of (geometric) measure theory.

Let $X \subseteq \mathbb {R}^N$ be a set. A positive measure $\mu$ on the $\sigma$-algebra of Borel sets in $X$ is a positive Radon measure if it is finite on compact sets; if it holds as well that $\mu (X)<+\infty$, we say that $\mu$ is a finite positive Radon measure. We denote the space of positive Radon measures on $X$ by $\mathscr {M}_{\rm loc}(X)$ and the one of finite positive Radon measures by $\mathscr {M}(X)$.

The Riesz representation theorem proves that $\mathscr {M}_{\rm loc}(X)$ may be identified as the dual of the space of compactly supported continuous functions $C_c(X)$ endowed with local uniform convergence. Accordingly, we say that a sequence $\{\mu _k\}\subset \mathscr {M}_{\rm loc}(X)$ converges to $\mu \in \mathscr {M}_{\rm loc}(X)$ in the local weak-$\ast$ sense, and we write $\mu _k\stackrel {\ast }{\rightharpoonup } \mu$ in $\mathscr {M}_{\rm loc}(X)$, if

(2.6)\begin{equation} \lim_{k\to+\infty} \int_{X} f(x)\,\mathrm{d}\mu_k(x) = \int_{X} f(x)\,\mathrm{d}\mu(x) \quad\text{for every}\ f\in C_c(X). \end{equation}

In wider generality, if $\mu _k\stackrel {\ast }{\rightharpoonup } \mu$ in $\mathscr {M}_{\rm loc}(X)$, then the previous equality holds for every bounded Borel function $f\colon X \to \mathbb {R}$ with compact support such that the set of its discontinuity points is $\mu$-negligible. In particular, if $X$ is compact and $\mu _k\stackrel {\ast }{\rightharpoonup } \mu$ in $\mathscr {M}_{\rm loc}(X)$, then (2.6) holds for every $f\in C(X)$.

A uniform control on the mass of each compact set along a sequence of Radon measures is sufficient to ensure local weak-$\ast$ precompactness: if $\{\mu _k\}$ is a sequence of positive Radon measures such that $\sup _k\{ \mu _k(C) : C\subset X\} <+\infty$ for every compact set $C \subset X$, then there exists a locally weakly-$\ast$ converging subsequence.

3. Proof of theorem 1.2

We devote this section to proving that the summability and decay conditions in (1.5) are sufficient to yield convergence of a subsequence of $\{\mathscr {F}_{\varepsilon} \}$. In particular, we are able to characterize the limiting functional, as (1.6) shows.

As a first step, by assuming that the kernels $\rho _{\varepsilon }$ satisfy (1.5) (actually, it suffices that the bound holds just for one $R>0$), we deduce that the energies $\widehat {\mathscr {F}}_{\varepsilon}$ in (2.3) are finite for every $\psi \in L^2_w(\mathbb {R}^N)$, provided $\varepsilon$ is small enough. This is an immediate consequence of the next lemma, which, in spite of its simplicity, will prove to be useful.

Lemma 3.1 For every $\varepsilon \in J$, let $\rho _{\varepsilon} \colon \mathbb {R}^N \to [0,\,+\infty )$ be measurable, and let us suppose that (1.5) holds for $R=1$. Then, for every $\xi \in \mathbb {R}^N$

\begin{align*} & \limsup_{\varepsilon \to 0} \int_{B(0,1)} \rho_{\varepsilon}( z)\frac{ 1 - \cos(z\cdot \xi )}{| z |^2} \,\mathrm{d} z \leq \frac{M}{2} |\xi|^2, \\ & \limsup_{\varepsilon \to 0} \int_{B(0,1)^c} \rho_{\varepsilon}( z)\frac{ 1 - \cos(z\cdot \xi )}{| z |^2} \,\mathrm{d} z \leq 2M, \end{align*}

where $M\geq 0$ is as in (1.5).

Proof. From (1.5) with $R=1$, it follows:

(3.1)\begin{equation} \limsup_{\varepsilon \to 0} \int_{B(0,1)} \rho_{\varepsilon}(z)\,\mathrm{d} z \leq M, \quad \limsup_{\varepsilon \to 0} \int_{B(0,1)^c} \frac{\rho_{\varepsilon}( z)}{| z |^2} \,\mathrm{d} z \leq M \end{equation}

We first focus on contributions in $B(0,\,1)$. Since $\sin (t) \leq t$ for $t \geq 0$, we have:

(3.2)\begin{equation} \frac{1 - \cos ( z \cdot \xi)}{| z |^2} = \frac{1}{|z|^2}\int_0^{| z \cdot \xi|} \sin(t) \,\mathrm{d} t \leq \frac{1}{2} (\widehat z\cdot \xi)^2, \end{equation}

where $\widehat {z}:= z/|z|$. By taking into account the first inequality in (3.1), we deduce:

\[ \limsup_{\varepsilon \to 0} \int_{B(0,1)} \rho_{\varepsilon}( z) \frac{1 - \cos(z\cdot \xi )}{| z |^2} \,\mathrm{d} z \leq \frac{| \xi |^2}{2} \limsup_{\varepsilon \to 0} \int_{B(0,1)} \rho_{\varepsilon}( z) \,\mathrm{d} z \leq \frac{M}{2} | \xi |^2. \]

Instead, far from the origin, we have:

\[ \limsup_{\varepsilon \to 0} \int_{B(0,1)^c} \rho_{\varepsilon}( z) \frac{1 - \cos(z\cdot \xi )}{| z |^2} \,\mathrm{d} z \leq 2 \limsup_{\varepsilon \to 0} \int_{B(0,1)^c} \frac{\rho_{\varepsilon}( z)}{| z |^2} \,\mathrm{d} z \leq 2M, \]

where we used the second estimate in (3.1).

For the second step towards the proof of theorem 1.2, it is convenient to introduce the following notation: for every $\xi \in \mathbb {R}^N$ and $\varepsilon \in J$, we let:

(3.3)\begin{equation} I_{\varepsilon}(\xi;A):= \int_{A} \rho_{\varepsilon}(z)\frac{1-\cos( z\cdot \xi)}{| z|^2} \,\mathrm{d} z, \quad\text{for all}\ \mathscr{L}^N-\text{measurable}\ A\subseteq \mathbb{R}^N. \end{equation}

By lemma 3.1, we know that, under condition (1.5), the functional $I_{\varepsilon} (\xi ;\mathbb {R}^N)$ grows at most as $1+|\xi |^2$. Then, recalling the formulation of the BBM formula in Fourier variables provided by lemma 2.1, in order to show that (1.6) holds, it suffices to characterize the pointwise limit of the family of integrals with respect to $z$ in (2.3), when regarded as functions of $\xi$, that is, of $\{I_{\varepsilon} (\,\cdot \,;\mathbb {R}^N)\}$. The next proposition takes care of this.

Note that in order to achieve the task that we have just outlined it is natural to regard $\{\rho _{\varepsilon} \}$ as a family of Radon measures and to take the limit of $\{I_{\varepsilon} (\,\cdot \,;\mathbb {R}^N)\}$ by appealing to some weak-$\ast$ compactness argument. Even though such compactness is actually available (see step 2 in the proof of proposition 3.2), the discontinuity of the function $z \mapsto (1-\cos (\xi \cdot z))/|z|^2$ prevents the results recalled in § 2.2 from being immediately viable. To circumvent such an obstacle, in the proof of proposition 3.2 we introduce an auxiliary parameter $\delta \in J$ to quantify the range of interactions (respectively short, medium or long), and we accordingly define two families of measures, which are meant to encode the limiting behaviour of $\{\rho _{\varepsilon} \}$ at different scales.

Proposition 3.2 If (1.5) holds, then there exist an infinitesimal sequence $\{\varepsilon _k\}\subset J$ and two finite Radon measures $\mu \in \mathscr {M}(\mathbb {S}^{N-1})$ and $\nu \in \mathscr {M}(\mathbb {R}^N)$ that depend only on $\{\rho _{\varepsilon _k}\}$ and such that for every $\xi \in \mathbb {R}^N$:

\[ \lim_{k\to +\infty} I_{\varepsilon_k}(\xi;\mathbb{R}^N)= \frac{1}{2} \int_{\mathbb{S}^{N-1}} |\xi \cdot \sigma|^2\,\mathrm{d}\mu(\sigma) + \int_{\mathbb{R}^N\setminus \{0\}} \frac{1-\cos( z\cdot \xi)}{|z|^2} \,\mathrm{d}\nu(z). \]

Proof. Let us fix $\delta \in J$. In order to compute the desired limit we part $\mathbb {R}^N$ in three regions: $B(0,\,\delta )$, $A_\delta$, and $B(0,\,\delta ^{-1})^c$, where $A_\delta := \{ z \in \mathbb {R}^N : \delta <|z|<\delta ^{-1}\}$. The proof is then divided into several steps: for each given $\delta \in J$ (except for a countable family of them, see step 2 below) we take the limits as $\varepsilon \to 0$ of $I_{\varepsilon} (\xi ;B(0,\,\delta ))$, $I_{\varepsilon} (\xi ;A_\delta )$, and $I_{\varepsilon} (\xi ;B(0,\,\delta ^{-1})^c)$. For the analysis of the first two terms the starting point is the observation that (1.5) implies for every $R>0$ the existence of $\bar \varepsilon _R\in J$ such that

(3.4)\begin{equation} \int_{B(0,R)} \rho_{\varepsilon}(z)\,\mathrm{d} z \leq M+1 \quad\text{for every}\ \varepsilon \in (0,\bar\varepsilon_R) \end{equation}

(cf. (3.1)). In the final step, we conclude by summing up the three contributions and taking the limit as $\delta \to 0$.

Step 1: long-range interactions. The term $I_{\varepsilon} (\xi ;B(0,\,\delta ^{-1})^c)$ is readily estimated by means of (1.5): for every $\delta \in J$ we have:

(3.5)\begin{equation} \limsup_{k\to+\infty} I_{\varepsilon_k}(\xi;B(0,\delta^{{-}1})^c)\leq 2M \delta^2. \end{equation}

Step 2: medium-range interactions. For all $\varepsilon \in J$, let us define the measure $\nu _{\varepsilon} := \rho _{\varepsilon} \mathscr {L}^N$ (cf. (1.7)). Let $\{R^{(n)}\}_{n\in \mathbb {N}}$ be a strictly increasing sequence of strictly positive real numbers. It follows from (3.4) that for every $n\in \mathbb {N}$ there exists $\eta ^{(n)}\in J$ such that it holds:

\[ \int_{B(0,R^{(n)})} \,\mathrm{d} \nu_{\varepsilon} = \int_{B(0,R^{(n)})} \rho_{\varepsilon}(z)\,\mathrm{d} z \leq M+1, \quad\text{for every}\ \varepsilon\in (0,\eta^{(n)}). \]

We can choose each $\eta ^{(n)}$ so that $\{\eta ^{(n)}\}$ is strictly decreasing. From the previous bound, for each $n\in \mathbb {N}$ we deduce the existence of a finite positive Radon measure $\nu ^{(n)}\in \mathscr {M}(B(0,\,R^{(n)}))$ and of a sequence $\{\varepsilon _k^{(n)}\}\subset (0,\,\eta ^{(n)})$ such that $\nu _{\varepsilon _k^{(n)}} \stackrel {\ast }{\rightharpoonup } \nu ^{(n)}$ weakly-$\ast$ in $\mathscr {M}(B(0,\,R^{(n)}))$. By grounding on this property, a diagonal argument yields the existence of a sequence $\{\varepsilon _k\}\subset J$ and of a Radon measure $\nu$ on $\mathbb {R}^N$ such that $\nu _{\varepsilon _k} \stackrel {\ast }{\rightharpoonup } \nu$ locally weakly-$\ast$ in $\mathscr {M}_{\rm loc}(\mathbb {R}^N)$. In particular, by the lower semicontinuity of the total variation with respect to the weak-$\ast$ convergence, since $M$ does not depend on $R$, we infer that $\nu$ is finite.

We next resort to a known property of Radon measures: if $\{E_\delta \}_{\delta \in J}$ is a family of pairwise disjoint Borel sets in $\mathbb {R}^N$ and if $\mu \in \mathscr {M}_{\rm loc}(\mathbb {R}^N)$, then $\mu (E_\delta )>0$ for at most countably $\delta \in J$ (see [3, p. 29]). By applying this property to the family $\{\partial A_\delta \}_{\delta \in J}$ and the measure $\nu$, we deduce that the set of discontinuity points of the function:

\[ \chi_\delta (z):= \begin{cases} 0 & \text{if}\ z\notin A_\delta, \\ 1 & \text{if}\ z\in A_\delta \end{cases} \]

is $\nu$-negligible for all $\delta \in J$, but those in a certain countable subset $C\subset J$. As a consequence, since $\{\nu _{\varepsilon _k}\}$ weakly-$\ast$ converges to $\nu$, the following equality holds for every $\delta \in J\setminus C$:

(3.6)\begin{align} \lim_{k\to +\infty} I_{\varepsilon_k}(\xi;A_\delta) & = \lim_{k\to +\infty} \int_{\mathbb{R}^N} \chi_{\delta}(z)\frac{1-\cos( z\cdot \xi)}{|z|^2} \,\mathrm{d} \nu_{\varepsilon_k}(z) \nonumber\\ & = \int_{A_\delta} \frac{1-\cos( z\cdot \xi)}{|z|^2} \,\mathrm{d} \nu(z). \end{align}

Step 3: short-range interactions. We adapt the approach of [19, Subsec. 1.1]. For a fixed $\delta \in J$ and each $\varepsilon \in J$ we define the Radon measure $\mu _{\varepsilon} ^{(\delta )}$ on $\mathbb {S}^{N-1}$ by setting:

\begin{align*} \mu_{\varepsilon}^{(\delta)}(E) & := \int_E \left(\int_0^\delta t^{N-1} \rho_{\varepsilon}(t \sigma)\,\mathrm{d} t\right) \mathrm{d}\mathscr{H}^{N-1}(\sigma)\\ & \qquad\qquad\text{for all}\ \mathscr{H}^{N-1}-\text{measurable sets}\ E\subset \mathbb{S}^{N-1}. \end{align*}

By means of the coarea formula we deduce from (3.4) with $R=1$ that definitively $\mu _{\varepsilon} ^{(\delta )}(\mathbb {S}^{N-1})\leq M+1$. Thus, for all $\delta \in J$, there exists an infinitesimal sequence $\{\varepsilon _k^{(\delta )}\}\subset J$ and a finite Radon measures $\mu ^{(\delta )}\in \mathscr {M}(\mathbb {S}^{N-1})$ such that $\mu _{\varepsilon _k^{(\delta )}}^{(\delta )}\stackrel {\ast }{\rightharpoonup } \mu ^{(\delta )}$ weakly-$\ast$ in $\mathscr {M}(\mathbb {S}^{N-1})$ as $k\to +\infty$. Note that it holds $\mu ^{(\delta )}(\mathbb {S}^{N-1})\leq M+1$ for every $\delta \in J$.

Next, by a Taylor expansion of the cosine in $0$ we obtain:

\begin{align*} I_{\varepsilon}(\xi;B(0,\delta)) & = \frac{1}{2}\int_{B(0,\delta)} \rho_{\varepsilon}(z)|\xi\cdot \widehat{z}|^2 \,\mathrm{d} z + \int_{B(0,\delta)} \rho_{\varepsilon}(z) O(|\xi|^3|z|) \,\mathrm{d} z \\ & = \frac{1}{2}\int_{\mathbb{S}^{N-1}} |\xi\cdot \sigma|^2 \,\mathrm{d} \mu_{\varepsilon}^{(\delta)}(\sigma) + \int_{B(0,\delta)} \rho_{\varepsilon}(z) O(|\xi|^3|z|) \,\mathrm{d} z. \end{align*}

Since $\sigma \mapsto |\xi \cdot \sigma |^2$ is a continuous function on $\mathbb {S}^{N-1}$, in view of the weak-$\ast$ convergence of $\{\mu _{\varepsilon _k^{(\delta )}}^{(\delta )}\}$ we can take the limit as $k\to +\infty$. Thus, for every $\delta \in J$, we find

(3.7)\begin{align} & \limsup_{k\to+\infty} I_{\varepsilon_k^{(\delta)}}(\xi;B(0,\delta))\notag\\ & \quad = \frac{1}{2}\int_{\mathbb{S}^{N-1}} |\xi\cdot \sigma|^2 \,\mathrm{d} \mu^{(\delta)}(\sigma) + \limsup_{k\to+\infty} \int_{B(0,\delta)} \rho_{\varepsilon_k^{(\delta)}}(z) O(|\xi|^3|z|) \,\mathrm{d} z. \end{align}

Step 4: limit as $\delta \to 0$. In order to achieve the conclusion, we need to take the limit as $\delta \to 0$ of the terms considered in steps 1–3.

To this aim, let us consider the sequence $\{\varepsilon _k\}\subset J$ and the set $C\subset J$ given in step 2. Let also $\{\delta _n\}_{n\in \mathbb {N}}\subset J\setminus C$ be an infinitesimal sequence. We observe that for any $n\in \mathbb {N}$, by reasoning as in step 3, we can inductively extract a subsequence $\{\varepsilon _k^{(n)}\}\subset \{\varepsilon _k^{(n-1)}\} \subset \{\varepsilon _k\}$ such that the sequence of measures $\mu _k^{(n)}:= \mu ^{(\delta _n)}_{\varepsilon _k^{(n)}}$ weakly-$\ast$ converges in $\mathscr {M}(\mathbb {S}^{N-1})$ to some $\mu ^{(\delta _n)}$. Step 3 yields as well the existence of an unrelabelled subsequence $\{\delta _n\}$ and of a Radon measure $\mu \in \mathscr {M}(\mathbb {S}^{N-1})$ such that the sequence $\{\mu ^{(\delta _n)}\}$ weakly-$\ast$ converges in $\mathscr {M}(\mathbb {S}^{N-1})$ to $\mu$.

Let us now define the diagonal sequence $\{\tilde \varepsilon _k\}$ by setting $\tilde \varepsilon _k:= \varepsilon _k^{(k)}$ for every $k\in \mathbb {N}$. Then, recalling (3.4), it follows from (3.7) that

(3.8)\begin{equation} \lim_{n\to+\infty}\limsup_{k\to+\infty} I_{\tilde \varepsilon_k}(\xi;B(0,\delta_n)) = \frac{1}{2}\int_{\mathbb{S}^{N-1}} |\xi\cdot \sigma|^2 \,\mathrm{d} \mu(\sigma). \end{equation}

We also note that by monotone convergence, we can take the limit also in (3.6):

(3.9)\begin{equation} \lim_{n\to+\infty}\lim_{k\to+\infty} I_{\tilde \varepsilon_k}(\xi;A_{\delta_n}) = \int_{\mathbb{R}^N\setminus\{0\}} \frac{1-\cos( z\cdot \xi)}{|z|^2} \,\mathrm{d} \nu(z). \end{equation}

Eventually, by collecting (3.5)–(3.9), we get

\begin{align*} & \lim_{k\to +\infty} I_{\tilde \varepsilon_k}(\xi;\mathbb{R}^N)\notag\\ & \quad = \lim_{n\to +\infty} \limsup_{k\to +\infty} \left[I_{\tilde \varepsilon_k}\left(\xi;B(0,\delta_n)\right) +I_{\tilde \varepsilon_k}(\xi;A_{\delta_n}) +I_{\tilde \varepsilon_k}\left(\xi;B(0,\delta_n^{{-}1})^c\right) \right], \end{align*}

from which the conclusion follows.

We are now in a position to prove theorem 1.2.

Proof Proof of theorem 1.2

Keeping in force the notation in (3.3), by lemma 3.1 we know that for $k$ sufficiently large $I_{\varepsilon _k}(\xi ;\mathbb {R}^N)$ grows at most as $1+|\xi |^2$. Proposition 3.2, instead, characterizes the pointwise limit of $\{I_{\varepsilon _k}(\,\cdot \,;\mathbb {R}^N)\}$, where $\{\varepsilon _k\}\subset J$ is a suitable infinitesimal sequence. Thus, for every $\psi \in L^2_w(\mathbb {R}^N)$, by dominated convergence, we deduce:

\[ \lim_{k\to+\infty} \widehat{\mathscr{F}}_{\varepsilon_k}(\psi)= \int_{\mathbb{R}^N}|\psi(\xi)|^2 \left[ \frac{1}{2} \int_{\mathbb{S}^{N-1}} |\xi \cdot \sigma|^2\,\mathrm{d}\mu(\sigma) + \int_{\mathbb{R}^N\setminus \{0\}} \frac{1-\cos( z\cdot \xi)}{|z|^2} \,\mathrm{d}\nu(z) \right] \mathrm{d} \xi \]

where $\mu \in \mathscr {M}(\mathbb {S}^{N-1})$ and $\nu \in \mathscr {M}(\mathbb {R}^N)$ are as in proposition 3.2. Formula (1.6) is then achieved by recalling that the Fourier transform is a one-to-one correspondence between $H^1(\mathbb {R}^N)$ and $L^2_w(\mathbb {R}^N)$, and by computations similar to the ones in the proof of lemma 2.1.

We are now only left to show that the right-hand side in (1.6) is finite for every $u\in H^1(\mathbb {R}^N)$. As for the gradient term, its finiteness is trivial. For what concerns the nonlocal term, we note that in view of lemma 3.1 and of the construction in proposition 3.2 there holds

\[ \int_{\mathbb{R}^N\setminus\{0\}}\frac{1-\cos(z\cdot\xi)}{|z|^2}\,\mathrm{d} \nu(z)\leq 2M(1+|\xi|^2) \]

pointwise in $\mathbb {R}^N$. Thus, we deduce

\[ \int_{\mathbb{R}^N} |\psi(\xi)|^2 \int_{\mathbb{R}^N\setminus\{0\}}\frac{1-\cos(z\cdot\xi)}{|z|^2}\,\mathrm{d} \nu(z) \,\mathrm{d}\xi \leq 2M \int_{\mathbb{R}^N}|\psi(\xi)|^2(1+|\xi|^2)\,\mathrm{d}\xi \]

for every $\psi \in L^2_w(\mathbb {R}^N)$. The claim follows then by the same computations as in lemma 2.1.

4. Necessary and sufficient conditions for the BBM formula

The goal of this section is to prove that conditions (i) and (ii) in theorem 1.1 are both sufficient and necessary for the BBM formula to hold. We first address the sufficiency by proving corollary 1.3, then we turn to the necessity, that is, to theorem 1.1.

4.1. Sufficiency

As we outlined in § 1, corollary 1.3 is an immediate consequence of the proof of theorem 1.2.

Proof Proof of corollary 1.3

Under the current assumptions, we know that there exist an infinitesimal sequence of $\{\varepsilon _k\}$ and two Radon measures $\mu \in \mathscr {M}(\mathbb {S}^{N-1})$ and $\nu \in \mathscr {M}(\mathbb {R}^N)$ such that (1.6) is satisfied.

In order to conclude, it now suffices to recall that the measure $\nu$ is the weak-$\ast$ limit of the sequence defined by (1.7) (see step 2 in the proof of proposition 3.2). We are currently supposing that such sequence weakly-$\ast$ converges to $\alpha \delta _0$ for a suitable $\alpha \geq 0$: then, necessarily, $\nu =\alpha \delta _0$ and the second integral on the right-hand side in (1.6) vanishes. The conclusion is thus achieved.

4.2. Necessity

We now focus on the proof of theorem 1.1, thus showing that the sufficient conditions devised in the previous subsection are also necessary for the BBM formula to hold. As before, we rely on the formulation in Fourier variables provided by lemma 2.1, or, in other words, we assume that (2.5) holds for every $\psi \in L^2_w(\mathbb {R}^N)$ and for a given measure $\lambda \in \mathscr {M}({\mathbb {S}^{N-1}}).$ We first show that such a nonlocal-to-local formula forces the restrictions of the kernels $\{\rho _{\varepsilon} \}$ to any large ball to belong definitively to $L^1$, while the integrals of $\rho _{\varepsilon} (z)/|z|^2$ on the complement of such balls need to become increasingly smaller (see (1.3)). Then, item (ii) in theorem 1.1 will be derived as well.

Proposition 4.1 Suppose that the convergence in (2.5) holds for every $\psi \in L^2_w(\mathbb {R}^N)$ and for a given measure $\lambda \in \mathscr {M}({\mathbb {S}^{N-1}})$. Then, there exists $M\geq 0$ depending only on $N$ and $\lambda$ such that for every $R>0$ condition (1.3) is satisfied.

Proof. Throughout the proof, $c_N$ is a generic positive constant that depends just on the dimension $N$ and whose value may change from line to line.

Let $\psi \in L^2_w(\mathbb {R}^N)\setminus \{0\}$ be a radial function. Then, there exists a measurable $v\colon [0,\,+\infty ) \to \mathbb {R}$ such that $\psi (\xi )=v(|\xi |)$ and that

(4.1)\begin{equation} 0<\int_0^{+\infty} t^{N-1}(1+t^2) v^2(t) \,\mathrm{d} t <{+}\infty. \end{equation}

We define

\[ \psi_R(\xi) := R^{N/2} \psi ( R \xi ) \quad\text{for all}\ R>0, \]

and we observe that a change of variables yields:

\[ \int_{\mathbb{R}^N} |\xi|^2 |\psi_R(\xi)|^2\,\mathrm{d} \xi = \frac{1}{R^2} \int_{\mathbb{R}^N} |\xi|^2 |\psi(\xi)|^2\,\mathrm{d} \xi . \]

By choosing $\psi =\psi _R$ in (2.5), we infer that

(4.2)\begin{align} \lim_{k\to+\infty}\int_{\mathbb{R}^N} | \psi_R (\xi) |^2 \int_{\mathbb{R}^N} \rho_{\varepsilon_k}(z)\frac{1 - \cos( z\cdot \xi)}{| z |^2} \,\mathrm{d} z \,\mathrm{d} \xi & \leq \lambda(\mathbb{S}^{N-1}) \int_{\mathbb{R}^N} |\xi|^2| |\psi_R(\xi)|^2\,\mathrm{d} \xi \nonumber\\ & = \frac{c}{R^2}, \end{align}

where $c:= c(\lambda,\,\psi )$ is a suitable constant. We exchange the integrals on the left-hand side of (4.2) by the Fubini theorem, and, for any fixed $z\in \mathbb {R}^N\setminus \{0\}$, recalling that $\widehat {z}=z/|z|$, we let $L_{\widehat z}$ be a rotation such that $\widehat {z} = L_{\widehat {z}}^{\mathrm {t}} e_1$, where the superscript $\mathrm {t}$ denotes transposition. A change of variables yields:

(4.3)\begin{align} \int_{\mathbb{R}^N} | \psi_R (\xi) |^2 \left( 1-\cos(z \cdot \xi) \right) \mathrm{d} \xi & = \int_{\mathbb{R}^N} | \psi_R (\xi) |^2 \left( 1 - \cos\left( |z| e_1 \cdot (L_{\widehat z}\xi) \right) \right) \mathrm{d} \xi \nonumber\\ & = \int_{\mathbb{R}^N} | \psi_R (\xi) |^2 \left( 1 - \cos( |z| e_1 \cdot \xi) \right) \mathrm{d} \xi \end{align}

(recall that $\psi _R$ is radial). By plugging (4.3) into (4.2), we obtain:

\[ \lim_{k\to+\infty}\int_{\mathbb{R}^N} \frac{\rho_{\varepsilon_k}( z)}{| z |^2} \int_{\mathbb{R}^N} | \psi_R (\xi) |^2 \left( 1 - \cos( |z| e_1 \cdot \xi) \right) \mathrm{d} \xi \mathrm{d} z \leq \frac{c}{R^2}. \]

From now on, we detail the argument for $N\geq 4$ only; the lower dimensional cases may be addressed by similar (but lighter) computations. First, we change variables to find

(4.4)\begin{equation} \lim_{k\to+\infty} \int_{\mathbb{R}^N} \frac{\rho_{\varepsilon_k}( z)}{| z |^{N+2}} \int_{\mathbb{R}^N} \left| \psi_R \left( \frac{\xi}{| z |} \right) \right|^2 \left( 1 - \cos( e_1 \cdot \xi) \right) \mathrm{d} \xi \,\mathrm{d} z \leq \frac{c}{R^2}. \end{equation}

Next, we rewrite the integral with respect to $\xi$ on the left-hand side of (4.4) by employing spherical coordinates: for $\sigma \in \mathbb {S}^{N-1}$ we consider $\vartheta _1,\,\dots,\,\vartheta _{N-2}\in [0,\,\pi ]$ and $\vartheta _{N-1} \in [0,\,2\pi )$ such that

\begin{align*} e_1 \cdot \sigma & = \cos(\vartheta_1), \\ e_i \cdot \sigma & = \cos(\vartheta_i)\prod_{j=1}^{i-1} \sin(\vartheta_j) \quad\text{for} i=2,\dots,N-1,\\ e_N \cdot \sigma & = \prod_{j=1}^{N-1} \sin(\vartheta_j). \end{align*}

By the coarea formula, recalling that $\psi _R(\xi )=R^{N/2}v(R|\xi |)$ for $v$ as above, it holds:

\begin{align*} & \int_{\mathbb{R}^N} \left| \psi_R \left( \frac{\xi}{| z |} \right) \right|^2 \left( 1 - \cos(e_1 \cdot \xi) \right) \mathrm{d} \xi \\ & \quad = R^N \int_0^{+\infty} v^2 \left( \frac{R}{| z | } t \right) t^{N-1} \int_{\mathbb{S}^{N-1}} \left( 1 - \cos(t e_1 \cdot \sigma) \right) \mathrm{d} \mathscr{H}^{N-1}(\sigma) \,\mathrm{d} t \\ & \quad = \int_0^{2\pi} \,\mathrm{d} \vartheta_{N-1} \prod_{j=2}^{N-2} \int_0^{\pi} \sin^{N-j-1}(\vartheta_{j}) \,\mathrm{d} \vartheta_{j} \\ & \quad\quad \cdot R^N \int_0^{+\infty} v^2 \left( \frac{R}{| z | } t \right) t^{N-1} \int_0^{\pi} \left[ 1 - \cos\left( t \cos(\vartheta_1) \right) \right] \sin^{N-2}(\vartheta_1) \,\mathrm{d} \vartheta_1 \,\mathrm{d} t \\ & \quad = c_N R^N \int_0^{+\infty} v^2 \left( \frac{R}{| z | } t \right) t^{N-1} \int_0^{\pi} \left[ 1 - \cos\left( t \cos(\vartheta) \right) \right] \sin^{N-2}(\vartheta) \,\mathrm{d} \vartheta \,\mathrm{d} t \\ & \quad = c_N R^N \int_0^{+\infty} v^2 \left( \frac{R}{| z | } t \right) t \int_{{-}t}^{t} \left(1 - \cos(s) \right) (t^2 - s^2)^{{(N-3)}/{2}} \,\mathrm{d} s \,\mathrm{d} t \end{align*}

Since the integrand in the last expression is positive, by restricting the domain of integration we find

(4.5)\begin{align} & \int_{\mathbb{R}^N} \left| \psi_R \left( \frac{\xi}{| z |} \right) \right|^2 \left( 1 - \cos(e_1 \cdot \xi) \right) \mathrm{d} \xi\notag\\ & \quad \geq c_N R^N \int_0^{+\infty} v^2 \left( \frac{R}{| z | } t \right) t^{N-2} \int_{-({t}/{2})}^{{t}/{2}} \left(1 - \cos(s) \right) \mathrm{d} s \,\mathrm{d} t \nonumber\\ & \quad \geq c_N R^N \int_0^{+\infty} v^2 \left( \frac{R}{| z | } t \right) t^{N-1} \left( 1 - \frac{2}{t} \sin\left(\frac{t}{2}\right) \right) \mathrm{d} t. \end{align}

Next, we proceed by splitting the interval $(0,\,+\infty )$ into two regions, and we analyse the corresponding integrals separately.

We observe that by a Taylor expansion around $0$ there exists $\alpha _0>0$ such that

\[ 1- \frac{2}{t} \sin\left(\frac{t}{2}\right) \geq \alpha_0 t^2 \quad\text{for every}\ t\in (0,1]. \]

Then, starting from (4.4) and taking into account (4.5), we infer

\begin{align*} \frac{c}{R^2} & \geq \limsup_{k\to+\infty}\int_{B(0,R)} \frac{\rho_{\varepsilon_k}( z)}{| z |^{N+2}} \int_{\mathbb{R}^N} \left| \psi_R \left( \frac{\xi}{| z |} \right) \right|^2 \left( 1 - \cos( e_1 \cdot \xi) \right) \mathrm{d} \xi \,\mathrm{d} z \\ & \geq \alpha_0 c_N R^N \limsup_{k\to+\infty} \int_{B(0,R)} \frac{\rho_{\varepsilon_k}( z)}{| z |^{N+2}} \int_{0}^{{|z|}/{R}} t^{N+1} v^2 \left( \frac{R}{| z |} t \right) \mathrm{d} t \,\mathrm{d} z \\ & = \frac{\alpha_0 c_N}{R^2} \limsup_{k\to+\infty} \int_{B(0,R)} \rho_{\varepsilon_k}( z ) \int_0^1 t^{N+1} v^2 ( t ) \,\mathrm{d} t \,\mathrm{d} z. \end{align*}

In conclusion, owing to (4.1), we find

\[ \limsup_{k\to+\infty}\int_{B(0,R)} \rho_{\varepsilon_k}( z ) \,\mathrm{d} z \leq M_0 \]

for a suitable $M_0:= M_0(N,\,\lambda,\,v)$ that is finite for each $v\neq 0$ in $(0,\,1)$.

We now turn to the contribution accounting for ‘large’ $|z|$. Note that there exists $\alpha _1>0$ such that

\[ 1- \frac{2}{t} \sin\left(\frac{t}{2}\right) \geq \alpha_1 \quad\text{for every}\ t>1. \]

Therefore, by estimates similar to the ones above, we obtain:

\begin{align*} \frac{c}{R^2} & \geq \limsup_{k\to+\infty} \int_{B(0,R)^c} \frac{\rho_{\varepsilon_k}( z)}{| z |^{N+2}} \int_{\mathbb{R}^N} \left| \psi_R \left( \frac{\xi}{| z |} \right) \right|^2 \left( 1 - \cos( e_1 \cdot \xi) \right) \mathrm{d} \xi \,\mathrm{d} z \\ & \geq \alpha_1 c_N R^N \limsup_{k\to+\infty} \int_{B(0,R)^c} \frac{\rho_{\varepsilon_k}( z)}{| z |^{N+2}} \int_{{|z|}/{R}}^{+\infty} t^{N-1} v^2 \left( \frac{R}{| z |} t \right) \mathrm{d} t \,\mathrm{d} z\\ & = \alpha_1 c_N \limsup_{k\to+\infty} \int_{B(0,R)^c} \frac{\rho_{\varepsilon_k}( z)}{| z |^2} \int_1^{+\infty} t^{N-1} v^2 ( t ) \,\mathrm{d} t \,\mathrm{d} z, \end{align*}

and, again by (4.1), we deduce

\[ \limsup_{k\to+\infty}\int_{B(0,R)^c} \frac{\rho_{\varepsilon_k}( z)}{| z |^2} \,\mathrm{d} z \leq \frac{M_1}{R^2} \]

for some $M_1:= M_1(N,\,\lambda,\,v)$ that is finite for each $v\neq 0$ in $\mathbb {R} \setminus [0,\,1]$.

To conclude the proof, we first optimize $M_0$ and $M_1$ with respect to $v$ and we choose as $M$ the largest of the two optima; note, in particular, that $M$ is finite and strictly positive, and depends only on the dimension of the space and on $\lambda (\mathbb {S}^{N-1})$.

Remark 4.2 Observe that, heuristically, inequality (4.2) has the same structure of a Poincaré inequality: the $L^2$-norm of a function on the left-hand side, the $L^2$-norm of its gradient on the right one. So, in a sense, the integral with respect to $z$ on the left-hand side may be regarded as the inverse of the Poincaré constant. The latter has a well-known scaling property: if $c_P(\Omega )$ denotes the Poincaré constant associated with a certain domain $\Omega$, then $c_P(R \Omega ) = Rc_P(\Omega )$, where $R\Omega := \{ x\in \mathbb {R}^N : x/R \in \Omega \}$. Such considerations motivated the choice of the scaling of the test function $\psi$ in the proof above (recall that there we work in Fourier variables).

With proposition 4.1 at hand, we are now in a position to prove theorem 1.1.

Proof Proof of theorem 1.1

Thanks to proposition 4.1, we know that item (i) holds. As a consequence, there is an infinitesimal sequence $\{\varepsilon _k\}$ such that the inequality in (1.5) holds, and we may invoke the compactness result in theorem 1.2. Thus, there exist a subsequence $\{\varepsilon _{k_n}\}$ and two Radon measures $\mu \in \mathscr {M}(\mathbb {S}^{N-1})$ and $\nu \in \mathscr {M}(\mathbb {R}^N)$ such that for every $u\in H^1(\mathbb {R}^N)$:

\[ \lim_{n\to +\infty} \mathscr{F}_{\varepsilon_{k_n}}[u] = \frac{1}{2}\int_{\mathbb{R}^N} \left[ \int_{\mathbb{S}^{N-1}} | \nabla u(x) \cdot \sigma |^2 \,\mathrm{d} \mu(\sigma) + \int_{\mathbb{R}^N\setminus\{0\}} \frac{| u (x+z) - u (x) |^2}{| z |^2} \,\mathrm{d} \nu(z) \right] \mathrm{d} x. \]

In particular, from the proof of theorem 1.2 we know that $\nu$ is the weak-$\ast$ limit in $\mathscr {M}_{\rm loc}(\mathbb {R}^N)$ of the subsequence $\{\nu _{k_n}\}$ defined by

(4.6)\begin{equation} \langle \nu_{k_n} , f \rangle := \int_{\mathbb{R}^N} \rho_{\varepsilon_{k_n}}(z) f(z) \,\mathrm{d} z \quad\text{for all}\ f\in C_c(\mathbb{R}^N). \end{equation}

Note that, in principle, the measures $\mu$ and $\lambda$ may differ. However, since we are assuming (1.2), for every $u\in H^1(\mathbb {R}^N)$ it must hold:

\begin{align*} & \int_{\mathbb{R}^N} \int_{\mathbb{S}^{N-1}} | \nabla u(x) \cdot \sigma |^2 \,\mathrm{d} \lambda(\sigma) \,\mathrm{d} x \\ & \quad= \frac{1}{2}\int_{\mathbb{R}^N} \left[ \int_{\mathbb{S}^{N-1}} | \nabla u(x) \cdot \sigma |^2 \,\mathrm{d} \mu(\sigma) + \int_{\mathbb{R}^N\setminus\{0\}} \frac{| u (x+z) - u (x) |^2}{| z |^2} \,\mathrm{d} \nu(z) \right] \mathrm{d} x. \end{align*}

By passing to Fourier variables as in the proof of lemma 2.1, the previous equality becomes

\begin{align*} & \int_{\mathbb{R}^N} |\psi (\xi) |^2 \int_{\mathbb{S}^{N-1}} | \xi \cdot \sigma |^2 \,\mathrm{d} \lambda(\sigma) \,\mathrm{d} \xi \\ & \quad= \int_{\mathbb{R}^N} |\psi(\xi)|^2 \left[ \frac{1}{2} \int_{\mathbb{S}^{N-1}} |\xi \cdot \widehat z|^2 \,\mathrm{d}\mu(z) + \int_{\mathbb{R}^N\setminus \{0\}} \frac{1-\cos( z\cdot \xi)}{|z|^2} \,\mathrm{d}\nu(z) \right] \mathrm{d} \xi \end{align*}

for every $\psi \in L^2_w(\mathbb {R}^N)$, whence, by the fundamental theorem of the calculus of variations and the continuity with respect to the $\xi$ variable, we deduce:

(4.7)\begin{align} \int_{\mathbb{S}^{N-1}} | \xi \cdot \sigma |^2 \,\mathrm{d} \lambda(\sigma) & = \frac{1}{2} \int_{\mathbb{S}^{N-1}} |\xi \cdot \widehat z|^2 \,\mathrm{d}\mu(z)\notag\\ & \quad + \int_{\mathbb{R}^N\setminus \{0\}} \frac{1-\cos( z\cdot \xi)}{|z|^2} \,\mathrm{d}\nu(z) \quad\text{for every}\ \xi\in\mathbb{R}^N. \end{align}

Then, by dividing (4.7) by $|\xi |^2$ and letting $|\xi |\to +\infty$, we obtain:

(4.8)\begin{equation} \int_{\mathbb{S}^{N-1}} | \widehat \xi \cdot \sigma |^2 \,\mathrm{d} \lambda(\sigma) = \frac{1}{2} \int_{\mathbb{S}^{N-1}} |\widehat \xi \cdot \widehat z|^2 \,\mathrm{d}\mu(z) \quad\text{for every}\ \widehat\xi\in\mathbb{S}^{N-1}. \end{equation}

By (4.7) and (4.8), it follows that necessarily

\[ \int_{\mathbb{R}^N\setminus \{0\}} \frac{1-\cos( z\cdot \widehat\xi)}{|z|^2} \,\mathrm{d}\nu(z) = 0 \quad\text{for every}\ \widehat\xi\in\mathbb{S}^{N-1}, \]

but since $z\mapsto (1-\cos ( z\cdot \widehat \xi ))/|z|^2$ is a positive function with support on the whole space for every $\widehat \xi \in \mathbb {S}^{N-1}$, we infer that the restriction of $\nu$ to $\mathbb {R}^N\setminus \{0\}$ is $0$. By the definition of Lebesgue integral, we obtain that for any $f\in C_c(\mathbb {R}^N)$

\[ \int_{\mathbb{R}^N} f(z) \,\mathrm{d} \nu(z) = \nu(\{0\}) f(0), \]

that is, $\nu =\alpha \delta _0$ for a suitable $\alpha \geq 0$.

Finally, we conclude the proof of item (ii) by observing that for any subsequence $\{\varepsilon _{k_n}\}$ the associated sequence of measures $\{\nu _{k_n}\}$ defined by (4.6) must converge weakly-$\ast$ to $\alpha \delta _0$, and hence the whole sequence $\{\nu _k\}$ converges.

Remark 4.3 For each $\lambda \in \mathscr {M}(\mathbb {S}^{N-1})$, let us define the positive semi-definite symmetric matrix:

\[ A_\lambda := \int_{\mathbb{S}^{N-1}} \sigma \otimes \sigma \,\mathrm{d} \lambda(\sigma). \]

By employing this notation, the functional $\mathscr {F}$ in (2.2) rewrites as

\[ \mathscr{F}[u]= \int_{\mathbb{R}^N} A_\lambda\nabla u\cdot\nabla u\,\mathrm{d} x \]

for every $u\in H^1(\mathbb {R}^N)$.

As we observed in the previous proof, under the assumptions of theorem 1.1 the measure $\lambda$ in (1.2) and the measure $\mu$ obtained by the compactness argument need not be the same. However, equality (4.8) expresses the fact that the associated matrices satisfy $A_\lambda = A_\mu / 2$.

5. Discussion and perspectives

In what follows, we first present an alternative formulation of condition (i) in theorem 1.1, and we then compare our results with previous ones in other contributions. In particular, we explain how some classes of kernels that have been considered in the literature are encompassed by our theory. We conclude by outlining possible future investigations.

5.1. Lévy conditions and reformulation of (i)

As we recalled in § 1, the research on nonlocal-to-local formulas has been focused on sufficient conditions. However, it must be mentioned that necessary conditions for the finiteness of the nonlocal energies in (1.1) have been devised as well, and they are sometimes referred to as Lévy conditions. It is indeed known that, when $u\in H^1(\mathbb {R}^N)$, an $\varepsilon$-uniform upper bound on the functionals in (1.1) entails a certain summability close to the origin and a decay at infinity. Precisely, the following can be shown:

Theorem 5.1 Suppose that for every $u\in H^1(\mathbb {R}^N)$ there exists $c:= c(u)\geq 0$ such that $\mathscr {F}_{\varepsilon} [u]\leq c$ for all $\varepsilon \in J$. Then, the family $\{\rho _{\varepsilon} \}$ fulfils the Lévy conditions, that is, there exists $M\geq 0$ such that

\[ \int_{B(0,1)} \rho_{\varepsilon}(z) \,\mathrm{d} z + \int_{B(0,1)^c} \frac{\rho_{\varepsilon}(z)}{| z |^2} \,\mathrm{d} z \leq M \quad\text{for every}\ \varepsilon\in J. \]

For a proof, we refer, e.g. to the recent contribution [12, Thm. 2.1] (the authors work under radiality assumptions on the kernels, but for the result at stake, this does not play a role). Alternatively, we note that the argument in the proof of proposition 4.1 may be adapted to establish the previous proposition: it is enough to work with a fixed test function $\psi \in L^2_w(\mathbb {R}^N)$.

When the bound in theorem 5.1 holds only asymptotically, that is, $\limsup _{\varepsilon \to 0} \mathscr {F}_{\varepsilon} [u]\leq c$, it can be shown that

(5.1)\begin{equation} \limsup_{\varepsilon\to 0} \int_{\mathbb{R}^N}\frac{\rho_{\varepsilon}(z)}{1+|z|^2}\,\mathrm{d} z\leq M. \end{equation}

Such bound is necessary but not sufficient for the one in (i): as a counterexample, consider for $N=1$ the constant family $\rho _{\varepsilon} \equiv 1$. As we observed in § 1, indeed, condition (i) may be regarded as a uniform decay requirement on the kernels. In more precise terms, the following holds:

Lemma 5.2 Condition (i) is equivalent to the following:

1. (i′) There exists $\tilde M\geq 0$ such that for every $R>0$ there holds

   (5.2)\begin{equation} \limsup_{k\to+\infty} \int_{\mathbb{R}^N}\frac{\rho_{\varepsilon_k}(z)}{R^2+|z|^2}\,\mathrm{d} z \leq\frac{\tilde M}{R^2}. \end{equation}

Proof. We first show that (1.3) implies (5.2). Fix $R>0$. After a change of variable, (1.3) rewrites as

\[ \limsup_{k\to+\infty}\left[ \int_{B(0,1)} \rho_{\varepsilon_k}(Rz)\,\mathrm{d} z + \int_{B(0,1)^c} \frac{\rho_{\varepsilon_k}( Rz)}{| z |^2} \,\mathrm{d} z \right] \leq \frac{M}{R^N}. \]

The conclusion follows then by observing that

\[ \int_{B(0,1)} \rho_{\varepsilon_k}(Rz)\,\mathrm{d} z + \int_{B(0,1)^c} \frac{\rho_{\varepsilon_k}( Rz)}{| z |^2} \,\mathrm{d} z\geq \int_{\mathbb{R}^N}\frac{\rho_{\varepsilon_k}(Rz)}{1+|z|^2}\,\mathrm{d} z \]

and by performing a further change of variables.

Conversely, assume that (5.2) holds. Then, for every $R>0$ a change of variable yields

\[ \limsup_{k\to +\infty}\int_{\mathbb{R}^N}\frac{\rho_{\varepsilon_k}(Rz)}{1+|z|^2}\,\mathrm{d} z\leq \frac{\tilde M}{R^N}. \]

Since the real function $t\mapsto {t^2}/{(1+t^2)}$ is increasing on the positive real line, we find

\begin{align*} \int_{\mathbb{R}^N}\frac{\rho_{\varepsilon_k}(Rz)}{1+|z|^2}\,\mathrm{d} z& \geq\frac12\int_{B(0,1)}\frac{\rho_{\varepsilon_k}(Rz)}{1+|z|^2}\,\mathrm{d} z+\int_{B(0,1)^c}\frac{|z|^2}{1+|z|^2}\frac{\rho_{\varepsilon_k}(Rz)}{|z|^2}\,\mathrm{d} z\\ & \geq \frac{1}{2}\left(\int_{B(0,1)} \rho_{\varepsilon_k}(Rz)\,\mathrm{d} z + \int_{B(0,1)^c} \frac{\rho_{\varepsilon_k}( Rz)}{| z |^2} \,\mathrm{d} z\right). \end{align*}

A further change of variable entails (1.3).

Remark 5.3 We observed that (5.1) is necessary for (1.3) to hold. On the contrary, a sufficient condition not involving the parameter $R$ is the following: there exists an infinitesimal family $\{\omega _{\varepsilon} \} \subset (0,\,+\infty )$ such that

(5.3)\begin{equation} \limsup_{\varepsilon\to 0} \int_{\mathbb{R}^N}\frac{\rho_{\varepsilon}(z)}{1+\omega_{\varepsilon}|z|^2}\,\mathrm{d} z <{+}\infty. \end{equation}

However, this condition is stronger than (i): to see this, given a family $\{\omega _{\varepsilon} \}$ as above, observe that for $N=1$ the kernels $\rho _{\varepsilon} (z) := \omega _{\varepsilon} ^{1/4}$ fulfil (1.3), but not (5.3).

5.2. $L^1$ and fractional kernels

In [5], the authors proved their nonlocal-to-local formula under the assumption that the kernels $\rho _{\varepsilon}$ are standard mollifiers. A more general version of their result is the following:

Theorem 5.4 (cf. Thm. 1 in [19])

Let $p\in (1,\,+\infty )$ be fixed. For every $\varepsilon \in J$, let $\rho _{\varepsilon} \colon \mathbb {R}^N\to [0,\,+\infty )$ be a function with $\| \rho _{\varepsilon} /2 \|_{L^1(\mathbb {R}^N)}=1$. Suppose also that for every $\delta >0$

(5.4)\begin{equation} \lim_{\varepsilon\to 0} \int_{B(0,\delta)^c} \rho_{\varepsilon}(z) \,\mathrm{d} z = 0. \end{equation}

Then, for any $u\in W^{1,p}(\mathbb {R}^N)$ there exists $c>0$ such that

\[ \int_{\mathbb{R}^N \times \mathbb{R}^N} \rho_{\varepsilon} (x-y) \frac{| u (x) - u (y) |^p}{| x - y |^p} \,\mathrm{d} y \,\mathrm{d} x \leq c \quad\text{for every}\ \varepsilon\in J. \]

Besides, there exist an infinitesimal sequence $\{\varepsilon _k\}\subset J$ and a positive Radon measure $\lambda$ on the unit sphere $\mathbb {S}^{N-1}$ that depends only on $\{\rho _{\varepsilon _k}\}$ such that $\int _{\mathbb {S}^{N-1}} \,\mathrm {d}\lambda = 1$ and

(5.5)\begin{align} \lim_{k\to+\infty} \frac{1}{2} \int_{\mathbb{R}^N \times \mathbb{R}^N} \rho_{\varepsilon_k}(x-y) \frac{| u (x) - u (y) |^p}{| x - y |^p} \,\mathrm{d} y \,\mathrm{d} x = \int_{\mathbb{R}^N} \int_{\mathbb{S}^{N-1}} | \nabla u(x) \cdot \sigma |^p \,\mathrm{d} \lambda(\sigma) \,\mathrm{d} x \end{align}

for every $u\in W^{1,p}(\mathbb {R}^N)$.

We now show how the class of kernels considered in the theorem above falls within our theory.

Example 5.5 ($L^1$ kernels)

Let $\{\rho _{\varepsilon} \}_{\varepsilon \in J}$ be a family of kernels as in theorem 5.4. A direct check shows that the normalization condition $\|\rho _{\varepsilon} /2\|_{L^1(\mathbb {R}^N)}=1$ implies (1.5). Besides, for every $f\in C_c(\mathbb {R}^N\setminus \{0\})$ there exists $\delta >0$ so small that

\[ \int_{\mathbb{R}^N\setminus \{0\}} \rho_{\varepsilon}(z)f(z) \,\mathrm{d} z = \int_{B(0,\delta)^c} \rho_{\varepsilon}(z)f(z) \,\mathrm{d} z. \]

It hence follows from (5.4) that

\[ \lim_{\varepsilon\to 0}\int_{\mathbb{R}^N\setminus \{0\}} \rho_{\varepsilon}(z)f(z) \,\mathrm{d} z = 0, \]

which entails, similarly to the proof of corollary 1.3, that the weak-$\ast$ limit of the associated sequence in (1.7) is a multiple of $\delta _0$.

As we commented in § 1, fractional kernels are not exactly covered by theorem 5.4. With the next example, we see how they fit in our framework.

Example 5.6 (Fractional kernels)

Given $s\in (0,\,1)$ and $u\in L^2(\mathbb {R}^N)$, the (normalized) $s$-Gagliardo seminorm of $u$ is defined by

\[ \mathscr{G}_s[u]:= \frac{1-s}{2}\int_{\mathbb{R}^N\times \mathbb{R}^N} \frac{| u (x) - u (y) |^2}{| x - y |^{N+2s}}\,\mathrm{d} y \,\mathrm{d} x. \]

Such functional corresponds to the one in (1.1) upon selecting:

\[ \varepsilon := 1-s, \quad \rho_{\varepsilon}(z)=\rho_{\varepsilon}^{\mathscr{G}}(z) := \frac{\varepsilon}{2|z|^{N-2\varepsilon}}. \]

Note that in this case $\rho _{\varepsilon} \notin L^1(\mathbb {R}^N)$. On the contrary, for every $\delta >0$ and for suitable $N$-depending constants $\alpha _0,\,\alpha _1>0$, we have:

\begin{align*} \int_{B(0,\delta)} \frac{\varepsilon}{2|z|^{N-2\varepsilon}} \,\mathrm{d} z & = \alpha_0 \delta^{2\varepsilon}, \\ \int_{B(0,\delta)^c} \frac{\varepsilon}{2|z|^{N-2\varepsilon+2}} \,\mathrm{d} z & = \alpha_1\frac{\varepsilon}{(1-\varepsilon)\delta^{2(1-\varepsilon)}}. \end{align*}

In particular, by taking, e.g. $M=2$, we see that (1.5) holds. Besides, for every $R>\delta >0$ we have:

\[ \lim_{\varepsilon\to 0} \int_{B(0,R)\setminus B(0,\delta)} \frac{\varepsilon}{2|z|^{N-2\varepsilon}} \,\mathrm{d} z = \alpha_0 \lim_{\varepsilon\to 0} (R^{2\varepsilon}-\delta^{2\varepsilon}) = 0, \]

whence, similarly to the previous example, we infer that $\{\rho _{\varepsilon} ^{\mathscr {G}}\}$ converges locally weakly-$\ast$ to a multiple of the Dirac delta in $0$ in the sense of Radon measures.

5.3. Future directions

In this paper, we provided sufficient and necessary conditions on a family of kernels $\{\rho _{\varepsilon} \}$ for the nonlocal functionals in (1.1) to converge to a variant of the Dirichlet integral for every $u\in H^1(\mathbb {R}^N)$. It is natural to wonder whether such characterization still holds for the more general functionals considered in [5]. We conjecture that this is the case. Namely, given a family of positive, measurable kernels $\{\rho _{\varepsilon} \}_{\varepsilon \in J}$, we conjecture that for any open set $\Omega \subseteq \mathbb {R}^N$ with Lipschitz boundary and for any $p\in [1,\,+\infty )$ the following conditions are necessary and sufficient for the BBM formula to hold for every $u\in W^{1,p}(\Omega )$ when $p>1$ or $u\in BV(\Omega )$ when $p=1$:

1. (i) there exists $M\geq 0$ such that for every $R>0$ it holds:

   \begin{align*} & \limsup_{\varepsilon\to0}\int_{B(0,R)} \rho_{\varepsilon}(z)\,\mathrm{d} z \leq M, \\ & \limsup_{\varepsilon\to0} \int_{B(0,R)^c} \frac{\rho_{\varepsilon}( z)}{| z |^p} \,\mathrm{d} z \leq \frac{M}{R^p} \quad\text{when}\ \Omega\ \text{is unbounded}; \end{align*}

2. (ii) there exists an infinitesimal sequence $\{\varepsilon _k\}\subset J$ such that the sequence of measures $\{\nu _k\}\subset \mathscr {M}_{\rm loc}(\mathbb {R}^N)$ defined as in (1.4) converges locally weakly-$\ast$ to $\alpha \delta _0$ in the sense of Radon measures for a suitable $\alpha \geq 0$.

We remind that it is known that the BBM formula fails when the boundary of $\Omega$ is not regular enough (see [19, Rmk. 1], and [13] on a possible remedy).

Naturally, for $p\neq 2$ and $\Omega \subsetneq \mathbb {R}^N$ the Fourier approach is not viable anymore (but when $p\neq 2$ and $\Omega = \mathbb {R}^N$ techniques of Fourier analysis may still be invoked by resorting to the Littlewood–Paley theory, as it is done in the recent contribution [6]). A possible strategy to establish the necessity of the previous conditions is to follow the proof of [12, Thm. 2.1] and employ rescaled test functions as in the proof of proposition 4.1.

A second research direction concerns the variational convergence of the nonlocal energies to local ones, in the same spirit as [19, Thm. 8 and Cor. 8]. For a thorough treatment of $\Gamma$-convergence we refer to the monograph [8]. It is not difficult to see that the conditions in corollary 1.3 are sufficient for the $\Gamma$-convergence of $\{\widehat {\mathscr {F}}_{\varepsilon} \}$ to $\widehat {\mathscr {F}}$ when it is known that the limiting function $u$ has Sobolev regularity; under this extra assumption, by the inverse Fourier transform, the $\Gamma$-convergence of $\{\mathscr {F}_{\varepsilon} \}$ to $\mathscr {F}$ is recovered. Proving that they are also necessary would require a refinement of proposition 4.1, again possibly resorting to the approach of [12, Thm. 2.1]; note, in particular, that in our analysis (1.3) is derived from a $\Gamma$-limsup type inequality (see (4.2)).

$\Gamma$-Convergence results are usually complemented by equi-coercivity statements, because in this way convergences of minima and minimizers are obtained thanks to the so-called fundamental theorem of $\Gamma$-convergence, see e.g. [8, Cor. 7.20]. Such results also have a role in devising the domain of the $\Gamma$-limit. The convergence properties of sequences of $L^p$ functions with equi-bounded nonlocal energy were considered already in [5, Thm. 4]; refined results in the same vein have been obtained in [18, Thm. 1.2 and 1.3] and, more recently, in [1, Thm. 4.2]. Another natural question that is left open from our analysis is what conditions on the kernels $\{\rho _{\varepsilon} \}$ are necessary and sufficient for such a compactness result to hold. It is expected that some requirement on the support of the measures $\mu$ in theorem 1.2 has to be enforced (cf. [19, Thm. 5] and [1, Thm. 3.1]).