Hostname: page-component-f554764f5-fr72s Total loading time: 0 Render date: 2025-04-21T11:07:16.585Z Has data issue: false hasContentIssue false
  • English
  • Français

A remark on the well-posedness of the modified KdV equation in L2

Part of: Infinite-dimensional Hamiltonian systems Equations of mathematical physics and other areas of application

Published online by Cambridge University Press:  22 November 2024

Justin Forlano Open the ORCID record for Justin Forlano [Opens in a new window]
Justin Forlano*
Affiliation:
School of Mathematics, The University of Edinburgh, and The Maxwell Institute for the Mathematical Sciences, James Clerk Maxwell Building, The King’s Buildings, Peter Guthrie Tait Road, Edinburgh EH9 3FD, United Kingdom Department of Mathematics, University of California, Los Angeles, California 90095, United States ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the real-valued modified KdV equation on the real line and the circle in both the focusing and the defocusing cases. By employing the method of commuting flows introduced by Killip and Vişan (2019), we prove global well-posedness in Hs for 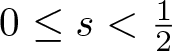$0\leq s \lt \tfrac{1}{2}$. On the line, we show how the arguments in the recent article by Harrop-Griffiths, Killip, and Vişan (2020) may be simplified in the higher regularity regime 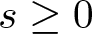$s\geq 0$. On the circle, we provide an alternative proof of the sharp global well-posedness in L2 due to Kappeler and Topalov (2005) and also extend this to the large-data focusing case.

Keywords

global well-posednessmodified Korteweg–de Vries equation

MSC classification

Primary: 35Q53: KdV-like equations (Korteweg-de Vries)
Secondary: 37K10: Completely integrable systems, integrability tests, bi-Hamiltonian structures, hierarchies (KdV, KP, Toda, etc.)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 26
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abdelouhab, L., Bona, J. L., Felland, M. and Saut, J. C.. Nonlocal models for nonlinear, dispersive waves. Phys.. 40 (1989), 360–392.Google Scholar
Bona, J. L. and Smith, R.. The initial-value problem for the Korteweg-de Vries equation. Philos. Trans. Roy. Soc. London Ser.. 278 (1975), 555–601.Google Scholar
Bourgain, J.. Fourier transform restriction phenomena for certain lattice subsets and applications to nonlinear evolution equations. II. The KdV equation. Geom. Funct. Anal. 3 (1997), 115–159.Google Scholar
Bourgain, J.. Periodic Korteweg-de Vries equation with measures as initial data. Selecta Math. (N.S.). 3 (1997), 115–159.CrossRefGoogle Scholar
Bringmann, B., Killip, R. and Vişan, M.. Global well-posedness for the fifth-order KdV equation in $H^{-1}(\mathbb{R})$. Ann. PDE. 7 (2021), .CrossRefGoogle Scholar
Chapouto, A.. A remark on the well-posedness of the modified KdV equation in the Fourier–Lebesgue spaces. Discrete Contin. Dyn. Syst. 41 (2021), 3915–3950.CrossRefGoogle Scholar
Chapouto, A.. A Refined well-posedness result for the modified KdV equation in the Fourier–Lebesgue spaces. J. Dynam. Differential Equations 35 (2023), 2537–2578.CrossRefGoogle ScholarPubMed
Christ, M., Colliander, J. and Tao, T.. Asymptotics, frequency modulation, and low regularity ill-posedness for canonical defocusing equations. Amer. J. Math. 125 (2003), 1235–1293.CrossRefGoogle Scholar
Christ, M., Colliander, J. and Tao, T.. Ill-posedness for nonlinear Schröodinger and wave equations. Preprint arXiv:math/0311048, 2003.Google Scholar
Christ, M., Holmer, J. and Tataru, D.. Low regularity a priori bounds for the modified Korteweg-de Vries equation. Lib. Math. (N.S.). 32 (2012), 51–75.Google Scholar
Colliander, J., Keel, M., Staffilani, G., Takaoka, H. and Tao, T.. Sharp global well-posedness for KdV and modified KdV on $\mathbb{R}$ and $\mathbb{T}$. J. Amer. Math. Soc. 16 (2003), 705–749.CrossRefGoogle Scholar
Guo, Z.. Global well-posedness of Korteweg-de Vries equation in $H^{-\frac{3}{4}}(\mathbb{R})$. J. Math. Pures Appl. 91 (2009), 583–597.CrossRefGoogle Scholar
Harrop-Griffiths, B., Killip, R., Ntekoume, M., and Vişan, M.. Global well-posedness for the derivative nonlinear Schrödinger equation in $L^2(\mathbb{R})$. J. Eur. Math. Soc. doi:10.4171/JEMS/1490.Google Scholar
Harrop-Griffiths, B., Killip, R. and Vişan, M.. Sharp well-posedness for the cubic NLS and mKdV in $H^{s}(\mathbb{R})$. Forum Math. 12 (2024), .Google Scholar
Harrop-Griffiths, B., Killip, R. and Vişan, M.. Large-data equicontinuity for the derivative NLS. Int. Math. Res. Not. .Google Scholar
Kappeler, T. and Molnar, J. -C.. On the well-posedness of the defocusing mKdV equation below L 2. SIAM J. Math. Anal. 49 (2017), 2191–2219.CrossRefGoogle Scholar
Kappeler, T. and Topalov, P.. Global well-posedness of mKdV in $L^2(\mathbb{T},\mathbb{R})$. Commun. Partial Differ. Equ. 30 (2005), 435–449.CrossRefGoogle Scholar
Kappeler, T. and Topalov, P.. Global wellposedness of KdV in $H^{-1}(\mathbb{T},\mathbb{R})$. Duke Math. J. 135 (2006), 327–360.CrossRefGoogle Scholar
Kato, T.. On the Korteweg-de Vries equation. Manuscripta Math. 28 (1979), 89–99.CrossRefGoogle Scholar
Kato, T.. On the Cauchy problem for the (generalized) Korteweg–de Vries equation. Studies in Applied Mathematics Adv. Math. Suppl. Stud., Vol.8, (Academic Press, New York, 1983).Google Scholar
Kenig, C., Ponce, G. and Vega, L.. On the (generalized) Korteweg-de Vries equation. Duke Math. J. 59 (1989), 585–610.CrossRefGoogle Scholar
Kenig, C., Ponce, G. and Vega, L.. Well-posedness and scattering results for the generalized Korteweg-de Vries equation via the contraction principle. Comm. Pure Appl. Math. 46 (1993), 527–620.CrossRefGoogle Scholar
Kenig, C., Ponce, G. and Vega, L.. On the ill-posedness of some canonical dispersive equations. Duke Math. J. 106 (2001), 617–633.CrossRefGoogle Scholar
Killip, R., Ntekoume, M. and Vişan, M.. On the well-posedness problem for the derivative nonlinear Schrödinger equation. Anal. PDE. 16 (2023), 1245–1270.CrossRefGoogle Scholar
Killip, R. and Vişan, M.. KdV is well-posed in H −1. Ann. of Math. 190 (2019), 249–305.CrossRefGoogle Scholar
Killip, R., Vişan, M. and Zhang, X.. Low regularity conservation laws for integrable PDE. Geom. Funct. Anal. 28 (2018), 1062–1090.CrossRefGoogle Scholar
Kishimoto, N.. Well-posedness of the Cauchy problem for the Korteweg-de Vries equation at the critical regularity. Differential Integral Equations. 22 (2009), 447–464.CrossRefGoogle Scholar
Kishimoto, N.. A remark on norm inflation for nonlinear Schrödinger equations. Commun. Pure Appl. Anal. 18 (2019), 1375–1402.CrossRefGoogle Scholar
Koch, H. and Tataru, D.. Conserved energies for the cubic nonlinear Schrödinger equation in one dimension. Duke Math. J. 167 (2018), 3207–3313.CrossRefGoogle Scholar
Kwon, S., Oh, T. and Yoon, H.. Normal form approach to unconditional well-posedness of nonlinear dispersive PDEs on the real line. Ann. Fac. Sci. Toulouse Math. 29 (2020), 649–720.CrossRefGoogle Scholar
Miura, R. M.. Korteweg-de Vries equation and generalizations. I. A remarkable explicit non- linear transformation. J. Mathematical Phys. 9 (1968), 1202–1204.CrossRefGoogle Scholar
Molinet, L.. Sharp ill-posedness results for KdV and mKdV equations on the torus. Adv. Math. 230 (2012), 1895–1930.CrossRefGoogle Scholar
Molinet, L., Pilod, D. and Vento, S.. Unconditional uniqueness for the modified Korteweg-de Vries equation on the line. Rev. Mat. Iberoam. 34 (2018), 1563–1608.CrossRefGoogle Scholar
Molinet, L., Pilod, D. and Vento, S.. On unconditional well-posedness for the periodic modified Korteweg-de Vries equation. J. Math. Soc. Japan. 71 (2019), 147–201.CrossRefGoogle Scholar
Nakanishi, K., Takaoka, H. and Tsutsumi, Y.. Local well-posedness in low regularity of the mKdV equation with periodic boundary condition. Discrete Contin. Dyn. Syst. 28 (2010), 1635–1654.CrossRefGoogle Scholar
Oh, T.. A remark on norm inflation with general initial data for the cubic nonlinear Schrödinger equations in negative Sobolev spaces. Funkcial. Ekvac. 60 (2017), 259–277.CrossRefGoogle Scholar
Pego, R. L.. Compactness in L 2 and the Fourier transform. Proc. Amer. Math. Soc. 95 (1985), 252–254.Google Scholar
Schippa, R.. On the existence of periodic solutions to the modified Korteweg-de Vries equation below $H^{\frac{1}{2}}(\mathbb{T})$. J. Evol. Equ. 20 (2020), 725–776.CrossRefGoogle Scholar
Takaoka, H. and Tsutsumi, Y.. Well-posedness of the Cauchy problem for the modified KdV equation with periodic boundary condition. Int. Math. Res. Not. 56 (2004), 3009–3040.CrossRefGoogle Scholar
Tao, T.. Multilinear weighted convolution of L 2-functions, and applications to nonlinear dispersive equations. Amer. J. Math. 123 (2001), 839–908.CrossRefGoogle Scholar
Tsutsumi, M.. Weighted Sobolev spaces and rapidly decreasing solutions of some nonlinear dispersive wave equations. J. Differential Equations. 42 (1981), 260–281.CrossRefGoogle Scholar