Radial solutions of a semilinear elliptic problem

Synopsis

We analyse the set of nonnegative, global, and radial solutions (radial solutions, for short) of the equation

where 0 < p < 1, and 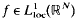is a radial and almost everywhere nonnegative function. We show that radial solutions of (E) exist if f(r) = o(r²p/1−1−p) or if f(r) ≈ cr^2p/1−p as r → ∞, where

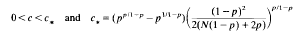
When f(r) = c_*r^2p/1−p + h(r) with h(r) = o(r^2p/1−p) as r → ∞, radial solutions continue to exist if h(r) is sufficiently small at infinity. Existence, however, breaks down if h(r) > 0,

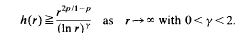
Whenever they exist, radial solutions are characterised in terms of their asymptotic behaviour as r → ∞.