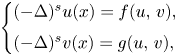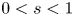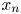1. Introduction
The work concerning qualitative properties of solutions was extensively investigated by many researchers. Fruitful results have been obtained on the existence, non-existence, symmetry and regularity and so on. Berestycki and Nirenberg [Reference Berestycki and Nirenberg3] obtained the monotonicity for the unbounded positive solutions of elliptic equations in the case of a ‘coercive’ Lipschitz graph. In [Reference Berestycki, Caffarelli and Nirenberg6], Berestycki et al. proved the monotonicity and uniqueness for elliptic equations in unbounded Lipschitz domains. Angenent [Reference Angenent1] and Clément and Sweers [Reference Clément and Sweers15] derived that a bounded positive solution of elliptic equations only depends on the $x_n$![]() -variable in a upper half space. Chen et al. [Reference Chen, Li and Li12] worked on the symmetry and non-existence of positive solutions of equations with fractional Laplacian in different types of domains. For more related results, please see [Reference Cabré and Tan7, Reference Chen, Fang and Yang10, Reference Chen and Li11, Reference Chen and Li14, Reference Gidas, Ni and Nirenberg18], and the references therein.
-variable in a upper half space. Chen et al. [Reference Chen, Li and Li12] worked on the symmetry and non-existence of positive solutions of equations with fractional Laplacian in different types of domains. For more related results, please see [Reference Cabré and Tan7, Reference Chen, Fang and Yang10, Reference Chen and Li11, Reference Chen and Li14, Reference Gidas, Ni and Nirenberg18], and the references therein.
In this work, we investigate the following system involving the fractional Laplacian:

in a bounded domain and an unbounded domain, respectively.
From an applicable point of view, the fractional Laplacian have caught researchers’ attention because of its non-locality and its applications in physical sciences. So far it has been utilized to model diverse physical phenomena, such as anomalous diffusion and quasi-geostrophic flows, turbulence and water waves, molecular dynamics and relativistic quantum mechanics of stars (see [Reference Bouchard and Georges5, Reference Caffarelli and Vasseur9, Reference Constantin16, Reference Tarasov and Zaslasvky22] and the references therein). It also has various applications in probability and finance [Reference Applebaum2, Reference Bertoin4]. In particular, the fractional Laplacian can be understood as the infinitesimal generator of a stable Lévy diffusion process [Reference Bertoin4].
The fractional Laplacian is a non-local pseudo-differential operator, taking the form
where $s\in (0,\,1)$![]() and PV stands for the Cauchy principal value. This operator is well defined for $u\in C^{\infty }_0(R^n)$
and PV stands for the Cauchy principal value. This operator is well defined for $u\in C^{\infty }_0(R^n)$![]() . In this space, it can also be defined equivalently in terms of the Fourier transform
. In this space, it can also be defined equivalently in terms of the Fourier transform
where $\mathcal {F}$![]() is the Fourier transform, and ${\mathcal {F}}^{-1}$
is the Fourier transform, and ${\mathcal {F}}^{-1}$![]() is the inverse Fourier transform. The fractional Laplacian can be extended to locally integrable functions with certain growth control—the weighted $L^1$
is the inverse Fourier transform. The fractional Laplacian can be extended to locally integrable functions with certain growth control—the weighted $L^1$![]() -space:
-space:
For $u\in \mathcal {L}_{2s}$![]() , we define $(-\Delta )^{s} u$
, we define $(-\Delta )^{s} u$![]() as a distribution:
as a distribution:
To investigate the properties of solutions of equations involving the fractional Laplacian, the method of moving planes and extension method [Reference Caffarelli and Silvestre8] have been powerful tools. In [Reference Zhuo, Chen, Cui and Yuan25], the authors employed the method of moving planes in integral forms (see [Reference Chen, Fang and Yang10, Reference Chen and Li11, Reference Chen, Li and Ou13] and the references therein) to study the symmetry of solutions. However, this method needs to establish the equivalence between the differential equations and the integral equations via Green's functions, and it is a challenge work. Also, this method depends heavily on some special properties of the corresponding Green's functions. So far, there are few results about the Green's functions in general domains. Chen et al. [Reference Chen, Li and Li12] developed a direct method of moving planes for the fractional Laplacian. Based on the classical sliding method for Laplacian [Reference Berestycki and Nirenberg3], Wu and Chen [Reference Wu and Chen23, Reference Wu and Chen24] developed the direct sliding method for the scalar equations involving the fractional Laplacian. Actually, the direct sliding method does not depend on the Green's functions. In this paper, we employ the direct sliding method [Reference Wu and Chen23, Reference Wu and Chen24] to derive the monotonicity of solutions of system (1.1) in a general bounded domain and an infinite cylinder.
The analogue problem to (1.1) for the fractional Laplacian has been investigated by many authors:

In the case $\Omega$![]() be a unit ball or half space, Mou [Reference Mou19] proved the symmetry and monotonicity of positive solutions of (1.3) by the integral equation approach. When $i=1,\,2$
be a unit ball or half space, Mou [Reference Mou19] proved the symmetry and monotonicity of positive solutions of (1.3) by the integral equation approach. When $i=1,\,2$![]() , $f_1=u^p_2$
, $f_1=u^p_2$![]() , $f_2=u^q_1$
, $f_2=u^q_1$![]() and $\Omega =R^n_+$
and $\Omega =R^n_+$![]() , Quaas and Xia [Reference Quaas and Xia20] obtained the non-existence of positive solutions of (1.3) by the method of moving planes with an improved Aleksandrov–Bakelman–Pucci type estimate for the fractional Laplacian.
, Quaas and Xia [Reference Quaas and Xia20] obtained the non-existence of positive solutions of (1.3) by the method of moving planes with an improved Aleksandrov–Bakelman–Pucci type estimate for the fractional Laplacian.
In this paper, we consider the non-linear equations involving the fractional Laplacian in general domains. Due to the non-local nature of the operator, we need to set exterior conditions in domain $\Gamma$![]() ,
,
In order to ensure the monotonicity of solutions, one has to impose the necessary exterior conditions (P) on $\Gamma$![]() : For any three points $x^1=(x',\,x^1_n)$
: For any three points $x^1=(x',\,x^1_n)$![]() , $x^2=(x',\,x^2_n)$
, $x^2=(x',\,x^2_n)$![]() and $x^3=(x',\,x^3_n)$
and $x^3=(x',\,x^3_n)$![]() with $x^1_n< x^2_n< x^3_n$
with $x^1_n< x^2_n< x^3_n$![]() , $x'\in {R}^{n-1}$
, $x'\in {R}^{n-1}$![]() , and $x^1$
, and $x^1$![]() , $x^3\in \Gamma ^c$
, $x^3\in \Gamma ^c$![]() , $x^1$
, $x^1$![]() , $x^2$
, $x^2$![]() and $x^3$
and $x^3$![]() satisfy
satisfy

We first study (1.1) in bounded domain $G$![]() , and establish monotonicity of solutions for (1.1) as following:
, and establish monotonicity of solutions for (1.1) as following:
Theorem 1.1 Let $u$![]() , $v\in \mathcal {L}_{2s}\cap C^{1,1}_{loc}(G)\cap C(\bar {G})$
, $v\in \mathcal {L}_{2s}\cap C^{1,1}_{loc}(G)\cap C(\bar {G})$![]() and $(u,\,v)$
and $(u,\,v)$![]() be a pair of solution for
be a pair of solution for

where $G$![]() is a convex bounded domain in $x_n$
is a convex bounded domain in $x_n$![]() direction, and $u$
direction, and $u$![]() , $v$
, $v$![]() satisfy the exterior condition $(\mathbf{P})$
satisfy the exterior condition $(\mathbf{P})$![]() on $G$
on $G$![]() . If $\frac {\partial f}{\partial v}>0$
. If $\frac {\partial f}{\partial v}>0$![]() , $\frac {\partial g}{\partial u}>0$
, $\frac {\partial g}{\partial u}>0$![]() for $x\in G$
for $x\in G$![]() , and $\frac {\partial f}{\partial u}$
, and $\frac {\partial f}{\partial u}$![]() , $\frac {\partial f}{\partial v}$
, $\frac {\partial f}{\partial v}$![]() , $\frac {\partial g}{\partial u}$
, $\frac {\partial g}{\partial u}$![]() , $\frac {\partial g}{\partial v}$
, $\frac {\partial g}{\partial v}$![]() are bounded from above in $G$
are bounded from above in $G$![]() , then $u$
, then $u$![]() and $v$
and $v$![]() are monotone increasing with respect to $x_n$
are monotone increasing with respect to $x_n$![]() -variable in $G$
-variable in $G$![]() . More precisely, for any $\tau >0$
. More precisely, for any $\tau >0$![]() , one has
, one has
In the proof of theorem 1.1, employing the argument by contradiction at extreme points, we first derive the key tool—narrow region principle in bounded domains. Combining with the sliding method, the solutions of system (1.4) are proved to be monotonic in the bounded domain $G$![]() . Next we briefly introduce the sliding method. For any positive real number $\tau$
. Next we briefly introduce the sliding method. For any positive real number $\tau$![]() , by sliding downward $\tau$
, by sliding downward $\tau$![]() units from the bounded domain $G$
units from the bounded domain $G$![]() , we have
, we have
here $e_n=(0,\,\dots,\,0,\,1)$![]() . Denote
. Denote

For $\tau$![]() sufficiently close to the width of $G$
sufficiently close to the width of $G$![]() in $x_n$
in $x_n$![]() direction, it is easy to see that $G\cap G_{\tau }$
direction, it is easy to see that $G\cap G_{\tau }$![]() is a narrow region. Applying the narrow region principle in bounded domains yields that
is a narrow region. Applying the narrow region principle in bounded domains yields that
Note that (1.5) provides a starting position to slide the domain $G_{\tau }$![]() . Then we slide $G_{\tau }$
. Then we slide $G_{\tau }$![]() back upward as long as inequality (1.5) holds to its limiting position. In fact, the domain should be slid to $\tau =0$
back upward as long as inequality (1.5) holds to its limiting position. In fact, the domain should be slid to $\tau =0$![]() . We conclude that the solutions of (1.4) are monotone increasing in $x_n$
. We conclude that the solutions of (1.4) are monotone increasing in $x_n$![]() variable.
variable.
Considering the unbounded domain $\Omega$![]() , because of the unboundedness property for $\Omega$
, because of the unboundedness property for $\Omega$![]() , the extremum points in $\Omega$
, the extremum points in $\Omega$![]() cannot be attained which makes it hard to apply the narrow region principle in unbounded domains directly. To overcome this difficulty, we first take a minimization sequence approaching to the infimum, and then make some perturbation about the sequence to attain the extremum points in some bounded domain. Combining with the iteration method, we can deduce the narrow region principle in unbounded domains. Then the monotonicity of solutions for (1.1) in an unbounded domain $\Omega$
cannot be attained which makes it hard to apply the narrow region principle in unbounded domains directly. To overcome this difficulty, we first take a minimization sequence approaching to the infimum, and then make some perturbation about the sequence to attain the extremum points in some bounded domain. Combining with the iteration method, we can deduce the narrow region principle in unbounded domains. Then the monotonicity of solutions for (1.1) in an unbounded domain $\Omega$![]() is obtained with the aid of the direct sliding method.
is obtained with the aid of the direct sliding method.
Theorem 1.2 Let $u$![]() , $v\in \mathcal {L}_{2s}\cap C^{1,1}_{loc}(R^n)$
, $v\in \mathcal {L}_{2s}\cap C^{1,1}_{loc}(R^n)$![]() be a pair of solution for
be a pair of solution for

where $\Omega =\{x=(x',\,x_n)\in R^n\,|\,0< x_n< M\}$![]() , $x'=(x_1,\,x_2,\,\dots,\,x_{n-1})$
, $x'=(x_1,\,x_2,\,\dots,\,x_{n-1})$![]() , and $M$
, and $M$![]() is a finite positive real number. $u,\,v$
is a finite positive real number. $u,\,v$![]() satisfy the exterior condition $(\mathbf{P})$
satisfy the exterior condition $(\mathbf{P})$![]() on $\Omega$
on $\Omega$![]() , and $u(x',\,\cdot )$
, and $u(x',\,\cdot )$![]() and $v(x',\,\cdot )$
and $v(x',\,\cdot )$![]() are bounded with $x'\in R^{n-1}$
are bounded with $x'\in R^{n-1}$![]() . Suppose that $\frac {\partial f}{\partial v}>0$
. Suppose that $\frac {\partial f}{\partial v}>0$![]() , $\frac {\partial g}{\partial u}>0$
, $\frac {\partial g}{\partial u}>0$![]() for $x\in \Omega$
for $x\in \Omega$![]() , and $\frac {\partial f}{\partial u}$
, and $\frac {\partial f}{\partial u}$![]() , $\frac {\partial f}{\partial v}$
, $\frac {\partial f}{\partial v}$![]() , $\frac {\partial g}{\partial u}$
, $\frac {\partial g}{\partial u}$![]() , $\frac {\partial g}{\partial v}$
, $\frac {\partial g}{\partial v}$![]() are bounded from above in $\Omega$
are bounded from above in $\Omega$![]() . Then $u(x)$
. Then $u(x)$![]() and $v(x)$
and $v(x)$![]() are monotone increasing in $x_n$
are monotone increasing in $x_n$![]() -variable, that is, for any $\tau >0$
-variable, that is, for any $\tau >0$![]() ,
,
Remark 1.3 Theorem 1.2 still holds if $\Omega$![]() is any domain bounded in the $x_n$
is any domain bounded in the $x_n$![]() -direction.
-direction.
One of the interesting point about the monotonicity of solutions is that it helps to pave the way for deriving existence, non-existence and some Sobolev inequalities, as can be seen in [Reference Chen, Li and Ou13, Reference Chen and Li14, Reference Dipierro, Soave and Valdinoci17] and the references therein.
This paper is organized as follows. In § 2, we establish some lemmas, such as the narrow region principle in bounded domains and so on. In § 3 and 4, combining the lemmas in § 2 with the sliding method, we derive the monotonicity of solutions for (1.1) on bounded domains and unbounded domains.
2. Key tools in the sliding method
The aim of this section is to show the key tools in the sliding method. More precisely, we investigate the narrow region principle in bounded domains and unbounded domains so that the sliding method can be initiated.
Lemma 2.1 Narrow region principle for system in bounded domains
Let $\tilde {U}$![]() , $\tilde {V}\in \mathcal {L}_{2s}\cap C^{1,1}_{loc}(E)$
, $\tilde {V}\in \mathcal {L}_{2s}\cap C^{1,1}_{loc}(E)$![]() satisfy
satisfy

where $E$![]() is a bounded domain, $c_1(x)>0$
is a bounded domain, $c_1(x)>0$![]() , $b_2(x)>0$
, $b_2(x)>0$![]() in $E$
in $E$![]() , and $b_i$
, and $b_i$![]() , $c_i$
, $c_i$![]() are bounded from above in $E$
are bounded from above in $E$![]() , $i=1,\,2$
, $i=1,\,2$![]() . Then for $d$
. Then for $d$![]() sufficiently small, which is the width of $E$
sufficiently small, which is the width of $E$![]() in $x_n$
in $x_n$![]() direction, one has
direction, one has
Proof. If (2.2) is not valid, then at least one of $\tilde {U}$![]() and $\tilde {V}$
and $\tilde {V}$![]() is less than zero at some point. We may assume that there exists a point $x^0\in E$
is less than zero at some point. We may assume that there exists a point $x^0\in E$![]() such that
such that
By (2.1), for $d$![]() sufficiently small, we have
sufficiently small, we have

This implies that
and
It follows from (2.4) that there exists some point $x^1\in E$![]() such that
such that
Similar to (2.3), we derive that, for $d$![]() sufficiently small,
sufficiently small,

Moreover, we get
Combining (2.5) and (2.7) yields that
Thus, one has
(2.9) is impossible for sufficiently small $d$![]() . Therefore, (2.2) holds.
. Therefore, (2.2) holds.
Lemma 2.2 Narrow region principle for system in unbounded domains
Let $D_1=\{x=(x',\,x_n)\in R^n|0< x_n<2l\}$![]() be an unbounded narrow region with some bounded constant $l$
be an unbounded narrow region with some bounded constant $l$![]() , and $D_-=\{x=(x',\,x_n)\in R^n|x_n<0\}$
, and $D_-=\{x=(x',\,x_n)\in R^n|x_n<0\}$![]() . If ${U}$
. If ${U}$![]() , ${V}\in \mathcal {L}_{2s}\cap C^{1,1}_{loc}(D_1)$
, ${V}\in \mathcal {L}_{2s}\cap C^{1,1}_{loc}(D_1)$![]() satisfy
satisfy

Suppose that $\bar {c}_1(x)>0$![]() , $\bar {b}_2(x)>0$
, $\bar {b}_2(x)>0$![]() in $D_1$
in $D_1$![]() , and $\bar {b}_i$
, and $\bar {b}_i$![]() , $\bar {c}_i$
, $\bar {c}_i$![]() are bounded from above in $D_1$
are bounded from above in $D_1$![]() , $i=1,\,2$
, $i=1,\,2$![]() . Then for $l$
. Then for $l$![]() sufficiently small, we get
sufficiently small, we get
Proof. The argument, by contradiction, is standard. Suppose (2.11) is false. Then at least one of ${U}(x)$![]() and ${V}(x)$
and ${V}(x)$![]() are less than zero at some points belonging to $D_1$
are less than zero at some points belonging to $D_1$![]() . Without loss of generality, we may assume that there are some points such that the values of $U$
. Without loss of generality, we may assume that there are some points such that the values of $U$![]() at these points are less than zero. Then there exists a sequence $\{x^k\}^{\infty }_{k=1}\subset D_1$
at these points are less than zero. Then there exists a sequence $\{x^k\}^{\infty }_{k=1}\subset D_1$![]() such that
such that
with $|x^k_n|< l$![]() , where $x^k_n$
, where $x^k_n$![]() is the $n$
is the $n$![]() -th component of $x^k$
-th component of $x^k$![]() .
.
Let

taking $a=e^{1/l}$![]() such that $\eta (0)=\max \limits _{R^n}\eta (x)=1$
such that $\eta (0)=\max \limits _{R^n}\eta (x)=1$![]() .
.
Set $\varphi _k(x)=\eta (x-x^k)$![]() . Combining with (2.12), there exists a positive sequence $\{\epsilon ^k\}^{\infty }_{k=1}$
. Combining with (2.12), there exists a positive sequence $\{\epsilon ^k\}^{\infty }_{k=1}$![]() such that
such that
where $\epsilon ^k\rightarrow 0$![]() as $k\rightarrow \infty$
as $k\rightarrow \infty$![]() .
.
Obviously, for $x\in R^n\setminus B_l(x^k)$![]() , $U(x)\geq A$
, $U(x)\geq A$![]() and $\varphi _k(x)=0$
and $\varphi _k(x)=0$![]() . Then we have
. Then we have
here $B_l(x^k)=\{x\in R^n\,|\,|x-x^k|< l\}$![]() .
.
Define $U_k(x)=U(x)-\epsilon ^k\varphi _k(x)$![]() . It follows from (2.15) that there exists some point $\bar {x}^k\in B_l(x^k)$
. It follows from (2.15) that there exists some point $\bar {x}^k\in B_l(x^k)$![]() such that
such that
It is easy to see that
and
Applying the first inequality of (2.10) and the definition of the fractional Laplacian, we derive

Then for sufficiently small $l$![]() and sufficiently large $k$
and sufficiently large $k$![]() , one has
, one has
This implies that
Based on (2.18), there exists a sequence $\{z^k\}^{\infty }_{k=1} \subset D_1$![]() such that
such that
Set $\psi _k(x)=\eta (x-z^k)$![]() . It is easy to see that
. It is easy to see that
and
Define $V_k(x)=V(x)-\epsilon ^k\psi _k(x)$![]() . It follows that there exists some point $\bar {z}^k\in B_l(z^k)$
. It follows that there exists some point $\bar {z}^k\in B_l(z^k)$![]() such that
such that
Similar to the proof of (2.16), by the second inequality of (2.10), we arrive at

For sufficiently small $l$![]() and sufficiently large $k$
and sufficiently large $k$![]() , we derive
, we derive
That is

By (2.17), we have
Combining (2.24) with (2.25), we derive

This yields
For sufficiently small $l$![]() , (2.27) is impossible.
, (2.27) is impossible.
This completes the proof of lemma 2.2.
3. Monotonicity of solutions in bounded domains
In this section, we will verify theorem 1.1.
The proof of theorem 1.1 Consider the following system:

where $G$![]() is a convex bounded domain in $x_n$
is a convex bounded domain in $x_n$![]() direction, and we denote the width of $G$
direction, and we denote the width of $G$![]() in $x_n$
in $x_n$![]() direction as $d$
direction as $d$![]() .
.
First we introduce some basic notations. For any positive real number $\tau$![]() , denote
, denote
here $x=(x_1,\,\dots,\,x_{n-1},\,x_n)=(x',\,x_n)$![]() , $e_n=(0,\,\dots,\,0,\,1)$
, $e_n=(0,\,\dots,\,0,\,1)$![]() , and
, and
Define
This proof consists of two steps.
Step 1. For $0<\tau < d$![]() sufficiently large, we want to show
sufficiently large, we want to show
By the exterior conditions (P) of $u$![]() and $v$
and $v$![]() , it is easy to see that
, it is easy to see that
This implies that we only need to prove
Applying the mean value theorem to the first equation of (3.1), we have
where $\xi ^{\tau }_1$![]() is between $u$
is between $u$![]() and $u^{\tau }$
and $u^{\tau }$![]() in $G$
in $G$![]() , and $\zeta ^{\tau }_1$
, and $\zeta ^{\tau }_1$![]() is between $v$
is between $v$![]() and $v^{\tau }$
and $v^{\tau }$![]() in $G$
in $G$![]() .
.
Similarly, we have
where $\xi ^{\tau }_2$![]() is between $u$
is between $u$![]() and $u^{\tau }$
and $u^{\tau }$![]() in $G$
in $G$![]() , and $\zeta ^{\tau }_2$
, and $\zeta ^{\tau }_2$![]() is between $v$
is between $v$![]() and $v^{\tau }$
and $v^{\tau }$![]() in $G$
in $G$![]() .
.
Note that $\Sigma _{\tau }$![]() is a narrow region for $0<\tau < d$
is a narrow region for $0<\tau < d$![]() sufficiently large. Applying lemma 2.1 to $\tilde {U}^{\tau }$
sufficiently large. Applying lemma 2.1 to $\tilde {U}^{\tau }$![]() and $\tilde {V}^{\tau }$
and $\tilde {V}^{\tau }$![]() with
with
we derive that (3.4) is valid. We conclude that (3.2) must hold.
Step 2. Now we decrease $\tau$![]() as long as (3.2) holds to the limiting position. Define
as long as (3.2) holds to the limiting position. Define
We want to prove
If $\tau _0>0$![]() , we can show that $G_{\tau _0}$
, we can show that $G_{\tau _0}$![]() can be slid upward a little bit and we still have, for some small $\delta >0$
can be slid upward a little bit and we still have, for some small $\delta >0$![]() and $\tau \in (\tau _0-\delta,\,\tau _0)$
and $\tau \in (\tau _0-\delta,\,\tau _0)$![]() ,
,
This contradicts with the definition of $\tau _0$![]() . Therefore, (3.7) holds. We postpone proving (3.8).
. Therefore, (3.7) holds. We postpone proving (3.8).
In fact, for $\tau _0>0$![]() , we can show that
, we can show that
Otherwise, at least one of $\min \limits _{x\in \Sigma _{\tau _0}}\tilde {U}^{\tau _0}(x)$![]() and $\min \limits _{x\in \Sigma _{\tau _0}}\tilde {V}^{\tau _0}(x)$
and $\min \limits _{x\in \Sigma _{\tau _0}}\tilde {V}^{\tau _0}(x)$![]() are equal to zero. We may assume that, there exists a point $\bar {x}\in \Sigma _{\tau _0}$
are equal to zero. We may assume that, there exists a point $\bar {x}\in \Sigma _{\tau _0}$![]() such that
such that
It follows from (3.5) that
On the other hand, by the exterior condition (P) of $u$![]() , we arrive at
, we arrive at
Combining (3.10) and (3.11) yields
This is a contradiction. Hence (3.9) is valid. It follows that
Next we can choose some closed $Q\subset \Sigma _{\tau _0}$![]() such that $\Sigma _{\tau _0}\setminus Q$
such that $\Sigma _{\tau _0}\setminus Q$![]() is a narrow region. Applying (3.12), we have
is a narrow region. Applying (3.12), we have
By the continuity of $\tilde {U}^{\tau }$![]() and $\tilde {V}^{\tau }$
and $\tilde {V}^{\tau }$![]() in $\tau$
in $\tau$![]() , we obtain, for some small $\delta >0$
, we obtain, for some small $\delta >0$![]() and $\tau \in (\tau _0-\delta,\,\tau _0)$
and $\tau \in (\tau _0-\delta,\,\tau _0)$![]() ,
,
Applying the exterior condition (P), we have, for some small $\delta >0$![]() and $\tau \in (\tau _0-\delta,\,\tau _0)$
and $\tau \in (\tau _0-\delta,\,\tau _0)$![]() ,
,
It follows from lemma 2.1 that for some small $\delta >0$![]() and $\tau \in (\tau _0-\delta,\,\tau _0)$
and $\tau \in (\tau _0-\delta,\,\tau _0)$![]()
Combining (3.14), (3.15) and (3.16), we derive that, for some small $\delta >0$![]() and $\tau \in (\tau _0-\delta,\,\tau _0)$
and $\tau \in (\tau _0-\delta,\,\tau _0)$![]() ,
,
This implies (3.8) holds. It follows that (3.7) must be true.
This completes the proof of theorem 1.1.
4. Monotonicity of solutions in unbounded domains
In this section, we study system (1.6). For convenience, we write down (1.6) again:

where $\Omega =\{x=(x',\,x_n)\in R^n\,|\,0< x_n< M\}$![]() , $x'=(x_1,\,x_2,\,\dots,\,x_{n-1})$
, $x'=(x_1,\,x_2,\,\dots,\,x_{n-1})$![]() . We will verify theorem 1.2.
. We will verify theorem 1.2.
Proof of theorem 1.2 First we introduce some necessary notations. For any $0\leq \tau \leq M$![]() , set
, set
Let
which is obtained by sliding $\Omega$![]() downward $\tau$
downward $\tau$![]() units in $x_n$
units in $x_n$![]() direction, $e_n=(0,\,0,\,\dots,\,0,\,1)$
direction, $e_n=(0,\,0,\,\dots,\,0,\,1)$![]() .
.
Set
The proof consists of three steps.
Step 1. For $0<\tau < M$![]() sufficiently large, we want to show that
sufficiently large, we want to show that
Obviously,
By the exterior condition (P) of $u$![]() and $v$
and $v$![]() , we get
, we get
It is easy to see that $u^{\tau }(x)$![]() and $v^{\tau }(x)$
and $v^{\tau }(x)$![]() satisfy the PDEs (4.1). Combining with the mean value theorem, we obtain
satisfy the PDEs (4.1). Combining with the mean value theorem, we obtain
where $\xi ^{\tau }_1$![]() is between $u$
is between $u$![]() and $u^{\tau }$
and $u^{\tau }$![]() in $\Omega$
in $\Omega$![]() , and $\zeta ^{\tau }_1$
, and $\zeta ^{\tau }_1$![]() is between $v$
is between $v$![]() and $v^{\tau }$
and $v^{\tau }$![]() in $\Omega$
in $\Omega$![]() .
.
Similarly, we have
where $\xi ^{\tau }_2$![]() is between $u$
is between $u$![]() and $u^{\tau }$
and $u^{\tau }$![]() in $\Omega$
in $\Omega$![]() , and $\zeta ^{\tau }_2$
, and $\zeta ^{\tau }_2$![]() is between $v$
is between $v$![]() and $v^{\tau }$
and $v^{\tau }$![]() in $\Omega$
in $\Omega$![]() .
.
For $\tau$![]() sufficiently close to $M$
sufficiently close to $M$![]() , $D_{\tau }$
, $D_{\tau }$![]() is narrow region in $x_n$
is narrow region in $x_n$![]() direction. Applying the ‘narrow region principle for system on unbounded domains’ (lemma 2.2), we arrive at
direction. Applying the ‘narrow region principle for system on unbounded domains’ (lemma 2.2), we arrive at
Combining (4.3) and (4.6), we derive that (4.2) must hold.
Step 2. (4.2) provides a starting point to carry out the sliding method. Now we decrease $\tau$![]() as long as (4.2) holds to the limiting position. Define
as long as (4.2) holds to the limiting position. Define
We will show that
Otherwise, suppose that $\tau _0>0$![]() , we can show that $\Omega _{\tau }$
, we can show that $\Omega _{\tau }$![]() can be slid upward a little bit and we still have, for some small $\delta >0$
can be slid upward a little bit and we still have, for some small $\delta >0$![]() ,
,
This is a contradiction with the definition of $\tau _0$![]() . Then (4.7) holds. We delay to prove (4.8).
. Then (4.7) holds. We delay to prove (4.8).
To prove (4.8), we first show that
If (4.9) is not true, then at least one of $\inf _{x\in D_{\tau _0}}U^{\tau _0}(x)$![]() and $\inf _{x\in D_{\tau _0}}V^{\tau _0}(x)$
and $\inf _{x\in D_{\tau _0}}V^{\tau _0}(x)$![]() is equal to zero. We may assume that
is equal to zero. We may assume that
Hence, there exists a sequence $\{x^k\}^{\infty }_{k=1}\subset D_{\tau _0}$![]() such that
such that
Set

choosing $a=e^{1/r}$![]() and $r=\frac {M-\tau _0}{2}$
and $r=\frac {M-\tau _0}{2}$![]() , such that $\eta (0)=\max \limits _{R^n}\eta (x)=1$
, such that $\eta (0)=\max \limits _{R^n}\eta (x)=1$![]() .
.
Let $\varphi _k=\eta (x-x^k)$![]() . There exists a positive sequence $\{\varepsilon _k\}$
. There exists a positive sequence $\{\varepsilon _k\}$![]() such that
such that
with $\varepsilon _k\rightarrow 0,$![]() as $k\rightarrow \infty$
as $k\rightarrow \infty$![]() .
.
For any $x\in D_{\tau _0}\setminus B_r(x^k)$![]() , $U^{\tau _0}(x)\geq 0$
, $U^{\tau _0}(x)\geq 0$![]() and $\varphi _k(x)=0$
and $\varphi _k(x)=0$![]() . It is easy to see that,
. It is easy to see that,
where $B_r(x^k)=\{x\in R^n\,|\,|x-x^k|< r\}$![]() .
.
It follows that there exists some point $\tilde {x}^k\in B_r(x^k)\cap D_{\tau _0}$![]() such that
such that
Combining (4.10) and (4.13) yields that
Obviously, as $k\rightarrow \infty$![]() ,
,
By (4.4), we derive that, for $k$![]() sufficiently large,
sufficiently large,

where $\xi ^{\tau _0}_1(\tilde {x}^k)$![]() is between $u(\tilde {x}^k)$
is between $u(\tilde {x}^k)$![]() and $u^{\tau _0}(\tilde {x}^k)$
and $u^{\tau _0}(\tilde {x}^k)$![]() , and $\zeta ^{\tau _0}_1(\tilde {x}^k)$
, and $\zeta ^{\tau _0}_1(\tilde {x}^k)$![]() is between $v(\tilde {x}^k)$
is between $v(\tilde {x}^k)$![]() and $v^{\tau _0}(\tilde {x}^k)$
and $v^{\tau _0}(\tilde {x}^k)$![]() .
.
On the other hand, employing the definition of the fractional Laplacian,

Set $u_k(x)=u(x+\tilde {x}^k)$![]() , $U^{\tau }_k(x)=U^{\tau }(x+\tilde {x}^k)$
, $U^{\tau }_k(x)=U^{\tau }(x+\tilde {x}^k)$![]() . By Arzel$\grave {a}$
. By Arzel$\grave {a}$![]() –Ascoli theorem, we have
–Ascoli theorem, we have
Hence, as $k\rightarrow \infty$![]() ,
,
Combining (4.15), (4.16) and (4.17), we deduce that, as $k\rightarrow \infty$![]() ,
,
Obviously, (4.18) holds unless
By (4.19), we derive
for any $m\in {N}^+$![]() .
.
Choosing $(x',\,x_n)\in \Omega$![]() , and taking $m$
, and taking $m$![]() large enough such that $(x',\,x_n+m\tau _0)\in \Omega ^c$
large enough such that $(x',\,x_n+m\tau _0)\in \Omega ^c$![]() , we apply the exterior condition on $u$
, we apply the exterior condition on $u$![]() to derive a contradiction with (4.20). Thus, (4.9) holds.
to derive a contradiction with (4.20). Thus, (4.9) holds.
Choosing sufficiently large $K\subset D_{\tau _0}$![]() such that $D_{\tau _0}\setminus K$
such that $D_{\tau _0}\setminus K$![]() is narrow in $x_n$
is narrow in $x_n$![]() direction. Combining (4.9) with the continuity of $U^{\tau }$
direction. Combining (4.9) with the continuity of $U^{\tau }$![]() and $V^{\tau }$
and $V^{\tau }$![]() in $\tau$
in $\tau$![]() , we derive that, for some small $\delta >0$
, we derive that, for some small $\delta >0$![]() ,
,
Meanwhile, applying the exterior condition (P), we have
Employing lemma 2.2, we derive
Combining (4.21) with (4.23), we obtain
This contradicts the definition of $\tau _0$![]() . Hence, (4.7) is valid. We conclude that $u$
. Hence, (4.7) is valid. We conclude that $u$![]() and $v$
and $v$![]() are increasing in $x_n$
are increasing in $x_n$![]() variable.
variable.
This completes the proof of theorem 1.2.
Acknowledgements
The research of Zhuo was partially supported by NSFC grants 12031012 and 11701207, Natural Science Foundation of He'nan Province of China 222300420499. The research of Lü was partially supported by the Institute of Modern Analysis-A Frontier Research Center of Shanghai.