Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lai, Baishun
and
Wang, Jing
2017.
A new proof of Dávila–Flores–Guerra’s result on existence of singular solutions.
Nonlinear Analysis: Real World Applications,
Vol. 33,
Issue. ,
p.
33.


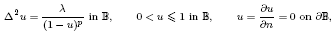
 is the unit ball in ℝ
is the unit ball in ℝ